FDR的定位原理
一、FDR定位原理概述
频域反射法(FDR)通过分析被测设备在频域上的反射特征,来推断时域(距离域)上的故障位置和性质。当电磁波信号沿着传输线进行传播时,如果遇到阻抗不连续点,一部分能量会继续向前传播,另一部分能量则会反射回来。反射的程度由反射系数(S11)决定。反射系数是反射信号与入射信号电压的比值,是一个复数,包含幅值和相位信号,表示反射信号的强度,
是反射系数的相位,表示反射信号对于入射信号的偏移。
相位是FDR定位的关键。信号从测试端传播到故障点再反射回来,会产生一个双程路径的延迟,将这个延迟转换为相位变化:
是信号的虚部,也为相位常数,它与频域f和电磁波在传输线的传播速度v有关
d是故障点到测试端的距离,且因为反射波滞后于入射波,所以带负号
因此,在某个频域f上测得的相位直接就包含了故障点的距离信息。
扫频仪在设定的频率范围内,以固定的离散频率点进行步进扫描,每个频点发送一个已知幅值和相位的正弦波信号到设备上,再测量反射信号的幅值和相位,计算该频点的S11。
将所有频率点上测量得到的S11收集起来,形成一个频域函数,称反射系数谱,对反射系数谱进行逆傅里叶变换,可以得到时域(空间域)函数S11(t),它代表的物理意义是设备在时域上的冲激响应。
二、定位原理推导

想要理解频域反射法,波的叠加是必须的,在式2.1中,m是频率采样点的索引,p和q是整数,代表不同距离的索引,对于特定距离点的反射,这个式子为频域反射信号提供了一个正交基,使得通过内积运算可以分离不同距离的反射贡献,从而在逆变换后能够映射到时域。

式2.2是离散傅里叶IDFT的标准形式,可以将数据转换到时域,具体来说
是频域采样点,包含频率f处的幅值和相位信息
是变换后得到的离散时域响应,表示信号在距离n处的反射强度。
m对应的每一个频率点。n是时域,是复指数基函数,最前的系数则是归一化因子。
而距离索引和距离具有对应关系,此变换将频域反射数据映射到距离域的脉冲响应,从而定位故障点的峰值。

式2.3描述了单故障情况下反射系数的精确表达式,公式的核心是相位延迟和信号衰减的组合,主要为相位和幅值得变换。
在式子的第一部分代表了幅值得衰减。
是故障点处初始反射系数,可以又FFT后得到每个频点位置对应的初始反射系数。开路时为1,短路时为-1.
是信号往返传播距离为2l的衰减系数。
中,2l/v是信号往返的时间,f是扫频其实的距离。
中的角度,就是
,括号内的内容代表的就是相对于起始频率的偏移量,也就是当前的频点的频率。将后半的式子用欧拉公式进行转换,以旋转因子表示可以得到
通过分析频点m反射系数的相位变化,就可以计算距离
在式2.2的逆变换中,我们也对式子进行欧拉公式变换,得到

也就是相位项与变换核发生共振,此时z(n)出现峰值,直接对应故障距离l。

在式子2.4中,我们对2.3取了共轭

在式子2.3中因为存在初始频率的固定相位项,利用共轭就可以将此项消除,可以得到

相位相处后,原式变为1,消除了初始频率带来的相位偏差,余下项只含有与m相关的线性相位,斜率可直接正比与距离l。
将式2.4简化为
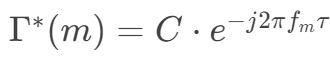
又知道逆变换公式为

代入共轭

将前面的常数项C提出求和符号可得到

定义相位差

只有满足匹配条件时,能得到对应的距离l,其余情况为0
