PCA(K-L变换)人脸识别（python实现）
数据集分析
ORL数据集， 总共40个人，每个人拍摄10张人脸照片
照片格式为灰度图像，尺寸112 * 92
特点：
-
图像质量高，无需灰度运算、去噪等预处理
-
人脸已经位于图像正中央，但部分图像角度倾斜（可以尝试五点定位进行透射变换统一视角）
任务介绍
人脸识别：将每个人10张图片中的6张用来构建训练集训练模型，10张中的2张作为验证集调参，剩余两张用于测试集验证效果。
分类任务：给出测试集的图片，需要准确判断出是谁的人脸（40类）
总流程介绍
训练过程
-
数据集划分
-
训练集上找PCA正交基，取前k个主要基
-
将训练集图片在这k个基上进行投影,特征向量，并且构建库
测试过程
-
新图片输入
-
根据训练集得到的正交基，在k个基上进行投影，得到特征向量
-
从库中进行匹配，找出最相似的k个，投票得出分类结果（knn）
方法介绍
K-L变换
不严谨的定义：从数据中找到k个正交基，使得以这k个基来表示图像的时候，最容易把图像之间彼此区分开。
推一下学长博客，解析的非常到位：
主成分分析法（离散K-L变换） - RyanXing - 博客园主成分分析法（离散K L变换） '主成分分析法（离散K L变换）' '1. 概述' '2. K L变换方法和原理推导' '2.1 向量分解' '2.2 向量估计及其误差' '2.3 寻找最小误差对应的正交向量系' '3. K L变换高效率的本质' '4. PCA在编、解码应用上的进一步推导' '4.
https://www.cnblogs.com/RyanXing/p/PCA.html
假设有一张100 * 100的图像，将图像拉平成一维，共有10000个自由的特征， 最原始的方法是对图像逐像素计算相似度。但是这样的相似度计算并不合理。因为在这1w维的向量里边有很多并不起作用（比如背景像素），也即有很多维度是冗余的。如果能够找到更精炼的匹配方法，分类的效果会更好
什么是数据的主要特征？
使用一组标准正交基表示n维空间里边的向量，大家习以为常：
对列向量x ,使用标准正交基{u} 去描述它，每一个维度的系数就是y
出于特征提取或者数据压缩等目的，常常采用 n维空间里边的一部分项去表示向量，比去取前d项
这样的截取虽然方便了我们去找主要影响因素，但是也损失了一些信息，我们希望损失的信息最少。
在均方损失意义下，损失公式如下（也就是向量每一个维度的估计值减去实际值的平方 最后加和），直观一点就是被舍弃的那些基分量的平方求和
造成损失的最终化简形式如下，中间的R矩阵是 向量 x 的自相关矩阵
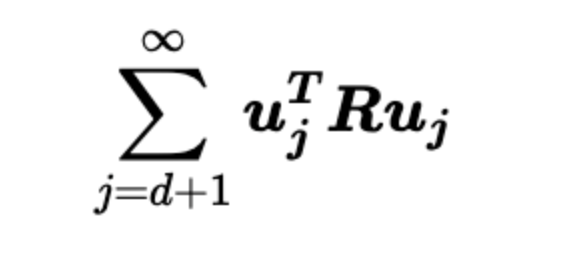
数学推导可以证明，这样的损失和选取的正交基有关，当选取R的特征向量构成的正交基的时候，这个误差就最小。
这就是K-L变换，最小均方误差意义下的最优正交变换。
K-L变换的运算方式
可以对上面的R矩阵硬进行分解，但是运算量非常大。
实际使用的时候大多中心化之后利用SVD加速，因为左奇异矩阵和右奇异矩阵的前若干个奇异值是相等的。
特征脸分析
使用PCA找到了前k个正交基，将这些向量还原回矩阵形式，可以观察到图片：这就被称为特征脸
结果展示
数据集划分：train:valid:test = 6:2:2
训练集共240个样本，经过SVD加速后只能取前240个特征向量，使用0.2的pca基保留率，最终剩下48个特征基
112 * 92 个值 压缩为 48 个值
验证集效果：正确率94.9986%
测试集效果：正确率93.7499%
完整代码链接（含数据）
完整代码链接，供交流学习使用，如有不足欢迎批评指正
GitHub - Keith1276/python_DIP_codeContribute to Keith1276/python_DIP_code development by creating an account on GitHub.https://github.com/Keith1276/python_DIP_code/tree/main