数据结构-排序-排序的七种算法（2）

一，七种算法的介绍和比较

二，冒泡排序

• 原理：重复遍历列表，比较相邻元素，如果顺序错误就交换它们

• 时间复杂度：

  • 最好：O(n)（已有序时）

  • 平均：O(n²)

  • 最坏：O(n²)

• 空间复杂度：O(1)

• 稳定性：稳定

• 特点：

  • 实现简单

  • 对部分有序数据效率较高

  • 每轮将最大元素"冒泡"到末尾

1.冒泡排序的基本思想：

• /*对顺序表L作交换排序（冒泡排序初级版）*/
  void Bubblesort0(SqList *L)
  {int i,j;for(i=1;i<L->length;i++){for(j=i+1;j<L->length;j++){if(L->r[i] > L->r[j]){swap(L,i,j);//交换L->r[i]与L->r[j]的值}}}
  }

  这个思想使用图表示：

• 

2.冒泡排序算法

/*对顺序表L作交换排序（冒泡排序初级版）*/
void Bubblesort(SqList *L)
{int i,j;for(i=1;i<L->length;i++){for(j=L->length-1;j>=i;j--){if(L->r[j] > L->r[j+1]){swap(L,i,j);//交换L->r[i]与L->r[j]的值}}}
}

 具体表现形式如图：

 当i=2时，变量j由8反向循环到2，逐个比较，在将关键字2交换到第二位置的同时，也将关键字4和3有所提升

3.冒泡排序优化

当我们待排序的序列是{2,1,3,4,5,6,7,8,9}，也就是说，除了第一和第二的关键字需要交换外，别的都已经是正常的顺序。当i=1时，交换了2和1，此时序列已经有序，但是算法仍然不停的循环将i=2到9以及每个循环中的j循环都执行了一遍，这样还会大大增加了算法计算的时间，如图

当i=2时，我们已经对9与8，8与7，.....3与2作了比较，没有任何数据交换，这就说明此序列已经有序，不需要再继续后面的循环判断工作了。

此时可以增加一个flag来实现这一算法的改进

/*对顺序表L作交换排序（冒泡排序初级版）*/
void Bubblesort2(SqList *L)
{int i,j;Status flag=TRUE;for(i=1;i<L->length&&flag;i++){flag=GALSE;for(j=L->length-1;j>=i;j--){if(L->r[j] > L->r[j+1]){swap(L,i,j);//交换L->r[i]与L->r[j]的值flag=TRUE;}}}
}

三，简单选择排序

1.核心思想

简单排序算法时一种直观但效率不高的比较排序算法。它的核心思想是：每次从未排序的部分中找到最小（或最大）的元素，然后将其放到已排序部分的末尾

简单使用代码说明：

void SelectSort(SqList *L)
{int i,j,min;for(i=1;i<L->Length;i++){min=1;for(j=i+1;j<=L->r[j])min=j;}if(i!=min){swap(L,i,min);}
}

 

2.时间复杂度分析

• 比较次数：无论数据初始状态如何，选择排序都需要进行大量的比较操作。

  • 第 1 趟：比较 n-1 次

  • 第 2 趟：比较 n-2 次

  • ...

  • 第 n-1 趟：比较 1 次

  • 总比较次数 = (n-1) + (n-2) + ... + 1 = n(n-1)/2

  • 因此，比较操作的时间复杂度为 O(n²)。

• 交换次数：选择排序的优点是交换次数相对较少。

  • 最好情况（数组已有序）：每趟循环都会发现 min_index == i，因此交换 0 次。

  • 最坏情况（数组逆序）：每趟都需要交换一次，共进行 n-1 次交换。

  • 平均情况下，也是大约 O(n) 次交换。

• 总时间复杂度：由于 O(n²) 的比较操作占主导地位，简单选择排序的平均和最坏情况时间复杂度都是 O(n²)。最好情况时间复杂度也是 O(n²)（因为比较次数仍然是 O(n²)，即使交换次数为 0）

3.优缺点分析

• 优点：

  • 思路简单直观，易于理解和实现。

  • 交换次数少。在数据移动成本较高时（例如要排序的数据是复杂对象），这可能是一个优点（相对于冒泡排序）。

  • 原地排序，不需要额外的存储空间（除了少量临时变量）。

• 缺点：

  • 时间复杂度高。O(n²) 的时间复杂度使其在处理大规模数据时效率低下。

  • 不稳定。如果需要保持相等元素的原始顺序，则不能使用简单选择排序。

  • 无论数据初始状态如何，比较次数几乎相同。即使输入数据已经有序或接近有序，它仍然需要进行 O(n²) 次比较。

四，直接插入排序

1.基本思想

这是一种简单直观且在实际应用中（特别是对小规模或基本有序的数据）表现不错的比较排序算法。其基本操作是：将一个记录插入到已经排好序的有序表中，从而得到一个新的，记录数增1的有序表

基本代码如下：

void InsertSort(SqList *L)
{int i,j;for(i=2;i<L->Length;i++){if(L->r[i] < L->r[i-1]){L->r[0]=L->r[i];for(j=i-1;L->r[j] > L->r[0];j--){L->r[i+1] = L->r[j];for(j=i-1;L->r[j] > L->r[0];j--)L->r[j+1]=L->r[j];L->r[j+1]=L->r[0];}}}
}

2.时间复杂度的分析

 3.优缺点分析

• 优点：

  • 简单直观，易于实现。

  • 对于小规模数据或基本有序的数据效率非常高（特别是 O(n) 的最好情况）。

  • 原地排序，空间效率高 (O(1))。

  • 稳定排序。

  • 适应性 (Adaptive)： 当输入数据部分有序时，实际运行时间接近 O(n)。

  • 在线性 (Online)： 可以一边接收新数据一边排序（因为排序过程是增量式的）。

• 缺点：

  • 平均和最坏情况时间复杂度为 O(n²)，不适合大规模随机数据。 当 n 较大时，效率显著低于 O(n log n) 的算法（如快排、归并、堆排）。

  • 元素移动操作较多。 每次插入都可能需要移动大量元素。

五，希尔排序

希尔排序是插入排序的高效改进版，由 Donald Shell 于 1959 年提出。它通过将原始列表分割成多个子序列进行预处理，大幅减少数据移动次数，显著提升排序效率。

1.核心思想

1. 分组插入：按特定增量（gap）将数组分割为若干子序列

2. 子序列排序：对每个子序列进行插入排序

3. 逐步缩小增量：重复上述过程，直至增量为 1（此时等同于标准插入排序）

4. 大跨度移动：早期使用大增量使元素大幅跳跃，减少小范围调整次数

算法代码如下：

void ShellSort(SqList *L)
{int i,j;int increment = L->length;do {increment=increment/3+1;//增量排序for(i=increment+1;i<=L->length;i++){if(i=increment+1;i<=L->length;i++){//需将L->r[i]插入有序增量子表L->r[0] = r[i];for(j=i-increment;j>0&&L->r[0] < L->r[j];j-=increment){L->r[j+increment] = L->r[j];}L->r[j+increment] = L->r[0];}}}while(increment>1);
}

代码解释如下：

 

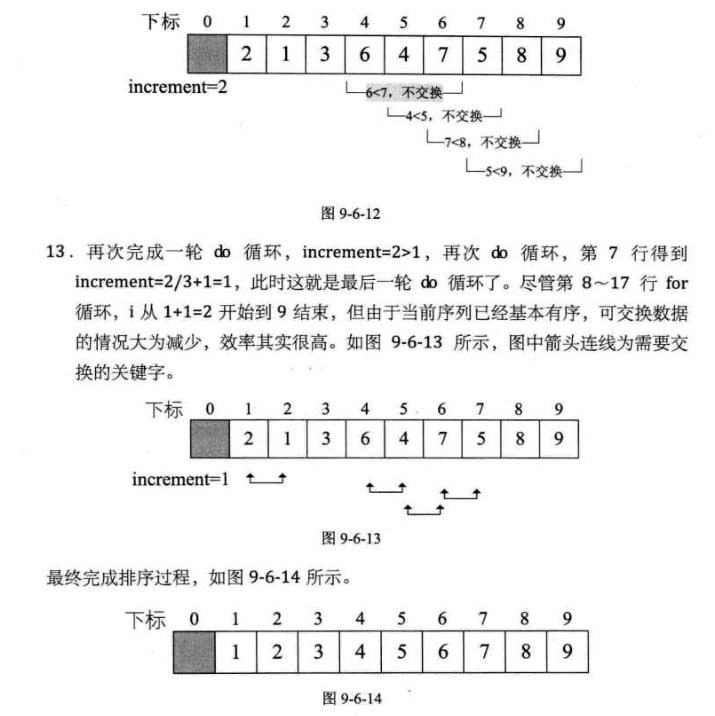
 2.优缺点

优点：

1. 突破 O(n²) 屏障，中等规模数据效率高

2. 原地排序，空间效率优异

3. 代码简洁（约 10 行核心代码）

4. 对部分有序数组效率接近 O(n)

缺点：

1. 时间复杂度依赖增量序列选择

2. 不稳定排序（需谨慎处理关键字段）

3. 大规模数据仍不如 O(n log n) 算法（如快速排序）

六，堆排序

1，基本概念

堆排序（Heap Sort）是一种高效的基于比较的排序算法，利用二叉堆的数据结构实现。它结合了插入排序和归并排序的优点：时间复杂度为 O(n log n)（最优、平均和最坏情况），空间复杂度为 O(1)（原地排序），且不需要递归栈（可迭代实现）。

2.核心概念

1. 二叉堆（Binary Heap）：

   • 完全二叉树结构（除最后一层外，所有层全满，最后一层从左向右填充）

   • 两种类型：

     • 最大堆：父节点值 ≥ 子节点值（根节点为最大值）

     • 最小堆：父节点值 ≤ 子节点值（根节点为最小值）

   • 存储方式：用数组表示，下标从 0 开始：

     • 父节点 i → 左子节点 2i+1，右子节点 2i+2

     • 子节点 i → 父节点 ⌊(i-1)/2⌋

2. 核心操作：

   • 堆化（Heapify）：调整子树使其满足堆性质。

   • 建堆（Build Heap）：将无序数组初始化为堆。

   • 排序：反复取出堆顶元素（极值）并调整堆。

3.算法步骤

• 建堆（Build Max Heap）：

  • 从最后一个非叶子节点开始（下标 n/2 - 1），向前遍历至根节点。

  • 对每个节点执行 下沉操作（Sift Down），使子树满足最大堆性质。

• 排序：

  • 将堆顶元素（最大值）与当前堆末尾元素交换。

  • 堆大小减 1（排除已排序的最大值）。

  • 对新的堆顶元素执行 下沉操作，恢复最大堆性质。

  • 重复上述过程，直到堆中只剩一个元素。

4.代码示例

#include <stdio.h>// 交换两个元素的值
void swap(int* a, int* b) {int temp = *a;*a = *b;*b = temp;
}// 下沉操作（最大堆）
void heapify(int arr[], int n, int i) {int largest = i;        // 初始化最大元素为当前节点int left = 2 * i + 1;   // 左子节点索引int right = 2 * i + 2;  // 右子节点索引// 如果左子节点大于当前节点if (left < n && arr[left] > arr[largest])largest = left;// 如果右子节点大于当前最大值if (right < n && arr[right] > arr[largest])largest = right;// 如果最大值不是当前节点，交换并继续堆化if (largest != i) {swap(&arr[i], &arr[largest]);heapify(arr, n, largest);  // 递归调整被交换的子树}
}// 堆排序主函数
void heapSort(int arr[], int n) {// 1. 构建最大堆（从最后一个非叶子节点开始）for (int i = n / 2 - 1; i >= 0; i--)heapify(arr, n, i);// 2. 逐个提取元素（堆排序核心）for (int i = n - 1; i > 0; i--) {// 将当前最大值（堆顶）移到数组末尾swap(&arr[0], &arr[i]);// 对剩余元素重新堆化（堆大小减1）heapify(arr, i, 0);}
}// 打印数组
void printArray(int arr[], int n) {for (int i = 0; i < n; ++i)printf("%d ", arr[i]);printf("\n");
}int main() {int arr[] = {12, 11, 13, 5, 6, 7};int n = sizeof(arr) / sizeof(arr[0]);printf("原始数组: ");printArray(arr, n);heapSort(arr, n);printf("排序后数组: ");printArray(arr, n);return 0;
}

 

代码解释

1. 关键函数说明

• swap()：交换两个整数的值

• heapify()：核心堆化操作

  • 确保以节点i为根的子树满足最大堆性质

  • 递归比较并交换父节点与子节点

• heapSort()：堆排序主函数

  • 第一步：构建最大堆（自底向上）

  • 第二步：反复提取堆顶元素并调整堆

2. 执行流程

以输入数组 [12, 11, 13, 5, 6, 7] 为例：

1. 构建最大堆：

   • 最后一个非叶子节点：n/2-1 = 6/2-1 = 2（即值13）

   • 从索引2开始向前处理：

     • 索引2（13）已满足堆性质

     • 索引1（11）：左子11<右子7 → 无需交换

     • 索引0（12）：左子11<13 → 与右子13交换

   • 最终堆：[13, 11, 12, 5, 6, 7]

2. 排序过程：

   步骤	操作	当前数组状态	剩余堆大小
   1	交换堆顶13与末尾7	[7, 11, 12, 5, 6, 13]	5
   	堆化剩余元素	[12, 11, 7, 5, 6, 13]
   2	交换堆顶12与末尾6	[6, 11, 7, 5, 12, 13]	4
   	堆化剩余元素	[11, 6, 7, 5, 12, 13]
   3	交换堆顶11与末尾5	[5, 6, 7, 11, 12, 13]	3
   	堆化剩余元素	[7, 6, 5, 11, 12, 13]
   4	交换堆顶7与末尾5	[5, 6, 7, 11, 12, 13]	2
   	堆化剩余元素	[6, 5, 7, 11, 12, 13]
   5	交换堆顶6与末尾5	[5, 6, 7, 11, 12, 13]	1

3. 最终结果：[5, 6, 7, 11, 12, 13]

5.优化方向

5.1 迭代版heapify：避免递归调用

void heapify_iterative(int arr[], int n, int i) {int largest = i;while (1) {int left = 2 * i + 1;int right = 2 * i + 2;if (left < n && arr[left] > arr[largest])largest = left;if (right < n && arr[right] > arr[largest])largest = right;if (largest == i) break;swap(&arr[i], &arr[largest]);i = largest;  // 移动到被交换的子节点}
}

5.2.减少交换次数

// 在heapify中使用
void sift_down(int arr[], int start, int end) {int root = start;while (2 * root + 1 <= end) {int child = 2 * root + 1;int swap_idx = root;if (arr[swap_idx] < arr[child])swap_idx = child;if (child + 1 <= end && arr[swap_idx] < arr[child + 1])swap_idx = child + 1;if (swap_idx == root) return;// 仅一次赋值操作int temp = arr[root];arr[root] = arr[swap_idx];arr[swap_idx] = temp;root = swap_idx;}
}

七，归并排序

1.基本思想

归并排序采用分治策略（Divide and Conquer）：

1. 分：将数组递归地分成两半

2. 治：对每个子数组进行排序

3. 合：将两个有序子数组合并为一个有序数组

2.算法步骤

1. 分解：将数组分成两个大小相等的子数组（奇数长度时允许差1）

2. 递归：对左右子数组递归进行归并排序

3. 合并：合并两个已排序的子数组

3.代码举例

#include <stdio.h>
#include <stdlib.h>void merge(int arr[], int l, int m, int r) {int n1 = m - l + 1;int n2 = r - m;int *L = malloc(n1 * sizeof(int));int *R = malloc(n2 * sizeof(int));for (int i = 0; i < n1; i++) L[i] = arr[l + i];for (int j = 0; j < n2; j++) R[j] = arr[m + 1 + j];int i = 0, j = 0, k = l;while (i < n1 && j < n2) {if (L[i] <= R[j]) arr[k++] = L[i++];else arr[k++] = R[j++];}while (i < n1) arr[k++] = L[i++];while (j < n2) arr[k++] = R[j++];free(L);free(R);
}void mergeSort(int arr[], int l, int r) {if (l < r) {int m = l + (r - l) / 2;mergeSort(arr, l, m);mergeSort(arr, m + 1, r);merge(arr, l, m, r);}
}

八，快速排序

1.基本思想

快速排序同样采用分治策略：

1. 分区：选择一个基准元素（pivot），将数组分为两部分

   • 左侧：所有元素 ≤ pivot

   • 右侧：所有元素 > pivot

2. 递归：对左右子数组递归进行快速排序

2.算法步骤

1. 选择基准元素（pivot）

2. 分区操作：将数组重新排列，使基准位于正确位置

3. 递归排序左子数组和右子数组

3.代码举例

#include <stdio.h>void swap(int* a, int* b) {int t = *a;*a = *b;*b = t;
}int partition(int arr[], int low, int high) {int pivot = arr[high];int i = (low - 1);for (int j = low; j <= high - 1; j++) {if (arr[j] < pivot) {i++;swap(&arr[i], &arr[j]);}}swap(&arr[i + 1], &arr[high]);return (i + 1);
}void quickSort(int arr[], int low, int high) {if (low < high) {int pi = partition(arr, low, high);quickSort(arr, low, pi - 1);quickSort(arr, pi + 1, high);}
}