振动分析 - 速度谱与加速度谱的转换
在平时查找资料时,我们会遇到一些实际采集到的振动频谱特征,比如:
115 留神坐标轴
周邵萍老师的这个案例分析中,出现的频谱图,纵坐标是速度。我们现在想看到它的加速度域的波形,此时:依照东南大学杨建刚老师的提示:5-6页,这些图表是启示性的
我们可以构建两张图表的转换程序。我们先由简谐振动公式,给出python转换程序:
1.简谐振动,位移速度加速度公式:
- 简谐振动:位移公式:
- 简谐振动:速度公式:
- 简谐振动:加速度公式:
注意,频谱中特定谱线对应的,都是标准的简谐振动,刚好可以用上述公式进行转换。因为振动在不同的视图下单位存在明显差异,所以,在转换过程中,要特别注意当前坐标轴的刻度。
1.1 相应的转换程序
#加速度谱转换速度谱,加速度数据已经经过折半处理
def gp_acc_spectrum_to_v_spectrum(fft_acc_halfed_yet, saps):fftScale = 1/saps*len(fft_acc_halfed_yet);arVelo = []arVelo.append(fft_acc_halfed_yet[0]*(2/fftScale)) #0点:恒定加速度,作用了2*1/saps*len(fft_acc)for i in np.arange(1, len(fft_acc_halfed_yet)):arVelo.append(fft_acc_halfed_yet[i]/(fftScale*np.math.pi*2*i))return arVelo#速度谱转换位移谱,速度数据已经经过折半处理
def gp_v_spectrum_to_s_spectrum(velo_halfed_yet, saps):return gp_acc_spectrum_to_v_spectrum(velo_halfed_yet, saps)#速度谱转换加速度谱,速度数据已经经过折半处理
def gp_v_spectrum_to_acc_spectrum(velo_halfed_yet, saps):fftScale = 1/saps*len(velo_halfed_yet);arAcc = []arAcc.append(0) #恒定速度对应的加速度为0for i in np.arange(1, len(velo_halfed_yet)):arAcc.append(velo_halfed_yet[i]*(fftScale*np.math.pi*2*i))return arAcc#位移谱转换速度谱,速度数据已经经过折半处理
def gp_s_spectrum_to_v_spectrum(s_halfed_yet, saps):return gp_v_spectrum_to_acc_spectrum(s_halfed_yet, saps)2.由速度谱构造加速度谱
我们试试将周老师的速度数据整理出来,绘制出速度谱和加速度谱:
100hz的谱线相对50Hz的谱线的比例,在加速度谱中会增大两倍,因为频率增大了两倍,相应角频率也是两倍关系。总体而言,就是加速度谱线中的高频部分,相较低频谱线会普遍抬升起来。

对照书中原有的速度谱:

2.1 两种频谱的转换源码:
class book_zhou_chap5_case2:def __init__(self):self.raw_mms_figure_data = [325,111,249,309,314,320,319,325,320] #pixel 补了零点self.raw_mms_figure_base = 325 #pixelself.mmpsScale = 160e-4/(325-85) #160um/s = 85pixelself.baseFreq = 50.5# 设置全局字体(需系统已安装对应字体)plt.rcParams['font.sans-serif'] = ['SimHei'] # 黑体plt.rcParams['axes.unicode_minus'] = False # 解决负号显示异常def showFigure(self):veloArray = [(325-item)*self.mmpsScale for item in self.raw_mms_figure_data]saps = 2*self.baseFreqaccArray = gp_vibration_helper.gp_v_spectrum_to_acc_spectrum(veloArray, saps)gArray = [acc/9.8 for acc in accArray]freqAxis = self.baseFreq* np.arange(len(veloArray))plt.figure(figsize=(12, 8))veloArrayIn_umps = [i*1e4 for i in veloArray]# 速度谱plt.subplot(2, 1, 1)plt.bar(freqAxis, veloArrayIn_umps, label='原始速度谱')plt.xlabel('频率 (Hz)')plt.ylabel('幅度 (um/s)')plt.legend()# 频域波形plt.subplot(2, 1, 2)plt.bar(freqAxis, gArray, label='加速度谱[推导] - in g')plt.xlabel('频率 (Hz)')plt.ylabel('幅值 (in g [9.8m/s^2])')plt.legend()plt.title = '速度谱 - 设备健康监测与故障诊断5-2.case2'plt.tight_layout()plt.show()app = book_zhou_chap5_case2()
app.showFigure()3.全息频谱
在进入PHM之后的振动分析,除了阈值分析外,还要进行故障的元器件定位,以及故障成因分析,所以,特别注重频域分析。除了时频图外,全息频谱是个有力的分析工具。它描述在这里:
5.1 全息频谱
我们现在利用西交大振动数据集,以及刚刚我们得到的加速度谱与速度谱之间的转换程序,来生成这个全息频谱(注意,最终的数据要转换至位移域,因为数据集的数据采样间隔太短,且单次采样数据量太少。我们只能给出全息包络谱——这种视图的每一个切片都是正圆):
3.1 源码
#3维模式展示一个频谱_推荐取振动的幅度值
def gp_showFFT_in3D(fft_freq, memo):if fft_freq is None: # 示例序列sequence = [1, 3, 2, 4, 5, 3, 2]else:sequence = fft_freq# 参数设置num_points = 100 # 每个圆的点数max_radius = 2.0 # 最大半径z_step = 1.0 # 相邻圆的高度差# 归一化半径min_val, max_val = min(sequence), max(sequence)radii = [(val - min_val)/(max_val - min_val)*max_radius + 0.1 for val in sequence]# 创建3D画布fig = plt.figure()ax = fig.add_subplot(111, projection='3d')ax.view_init(elev=163, azim=175, roll=0)# 绘制每个圆for i, r in enumerate(radii):theta = np.linspace(0, 2*np.pi, num_points)x = r * np.cos(theta)y = r * np.sin(theta)z = i * z_step * np.ones_like(theta)ax.plot(x, y, z, color='blue', alpha=0.6)# 连接相邻圆形成筒状表面for i in range(len(radii)-1):theta = np.linspace(0, 2*np.pi, num_points)x1 = radii[i] * np.cos(theta)y1 = radii[i] * np.sin(theta)z1 = i * z_step * np.ones_like(theta)x2 = radii[i+1] * np.cos(theta)y2 = radii[i+1] * np.sin(theta)z2 = (i+1) * z_step * np.ones_like(theta)ax.plot_surface(np.array([x1, x2]), np.array([y1, y2]), np.array([z1, z2]), color='gray', alpha=0.4)plt.title(f"Holographic 3D Envelope Spectrum {memo}")ax.set_xlabel('X')ax.set_ylabel('Y')ax.set_zlabel('Z')plt.show()3.2 西交大轴承数据库的一个全息频谱包络图
3.2.1 位移频谱包络

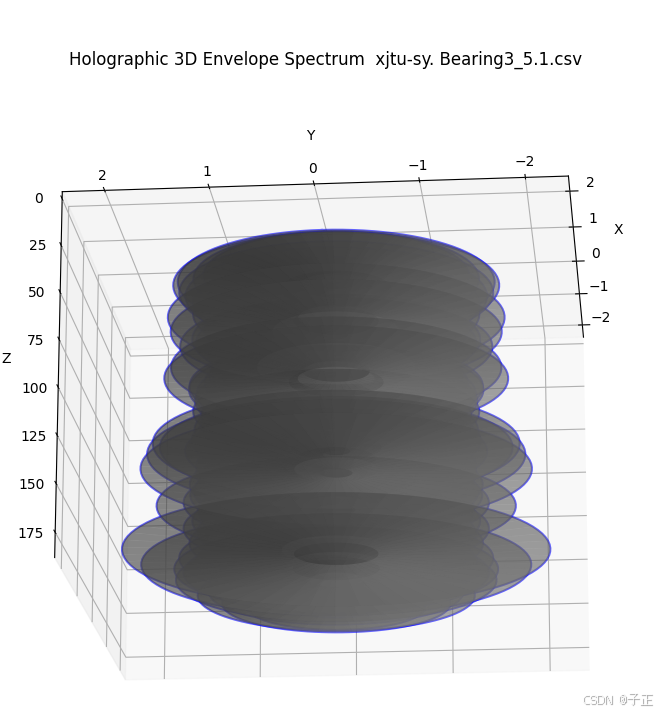
很像个蘑菇,对吧?最开始的蘑菇是这样的:
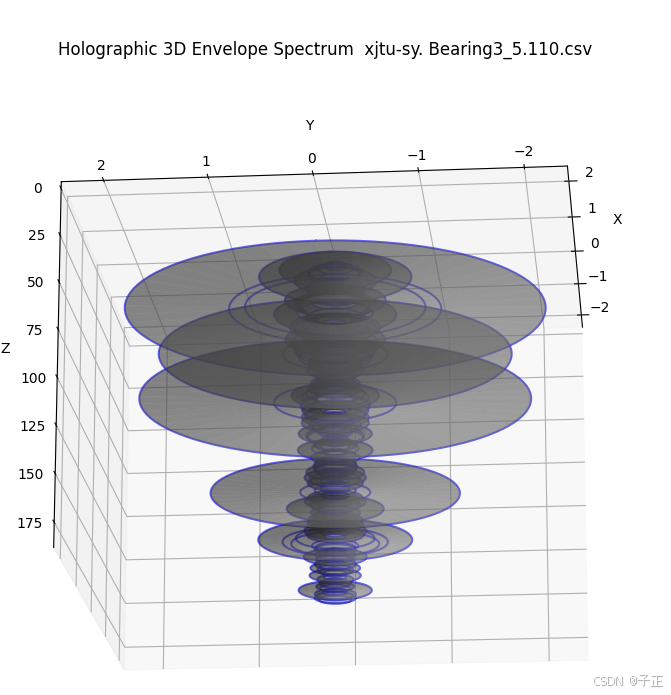
 稍稍高频部分的第二重伞盖开始张开时,系统已经出错了。终末期的伞盖是这样的:
稍稍高频部分的第二重伞盖开始张开时,系统已经出错了。终末期的伞盖是这样的:

这类故障高频部分的特征谱线根据前面的描述:加速度视图其实更明显,比如同样的第75笔数据,加速度频谱包络:
3.2.2 加速度频谱包络
最初,这个图样没有想到,这是高斯噪声在起作用:
终末期:
西交大的数据集中数据点数是足够多的,依次采集时间也足够长,真实的全息频谱是能够给出的。这个可以自行计算,那个时候,每一层圆环,会由一个单一的半径转变为指向不同相位的轨迹。最终能完整地描绘出振动体的优势振动方向,以及各个频点的相位关系。
然后上面的振动已经归一化,应该可以再引入颜色,标记其实际的振动,最终的效果就是这个蘑菇随着时间的延续会变得越来越亮。。。

