矩阵链乘法问题

问题介绍

给定𝑛个矩阵$A_1,A_2,\dots ,A_n$且$A_i$的维数为$p_{i-1}\times p_i$ (1 ≤ 𝑖 ≤ 𝑛)，以一种最小化标量乘法次数的方式进行完全括号化。

①设$A_{p\times q},A_{q\times r}$两矩阵相乘，这里定义普通乘法次数为𝑝 × 𝑞 × 𝑟;
②加括号多乘法次数的影响：

穷举法

列举出所有可能的计算次序，并计算出每一种计算次序相应需要的数乘次数，从中找出一
种数乘次数最少的计算次序。

用𝑝(𝑛)表示𝑛个矩阵链乘的穷举法计算成本，如果将𝑛个矩阵从第𝑘和第𝑘 + 1处隔开，对两个子序列再分别加扩号，则可以得到下面递归式：

动态规划法

步骤1：分析最优解的结构，划分子问题

矩阵链乘问题满足最优性原理：记𝐴[𝑖:𝑗]为$A_i{A}_{i+1}\dots A_j$链乘的一个最优括号方法，设𝐴[𝑖:𝑗]的最优次序中含有二个子链𝐴[𝑖: 𝑘]和𝐴[𝑘 + 1:𝑗]，则𝐴[𝑖: 𝑘]和𝐴[𝑘 + 1:𝑗]也是最优的。（反证法可得）

矩阵链乘的子问题空间𝑨 𝒊:𝒋 (𝟏 ≤ 𝒊 ≤ 𝒋 ≤ 𝒏):

步骤2：递归求解最优解的值

记𝑚[𝑖:𝑗]为计算𝐴[𝑖:𝑗]的最少乘法次数，则原问题的最优值为𝑚 1 [𝑛]，那么有：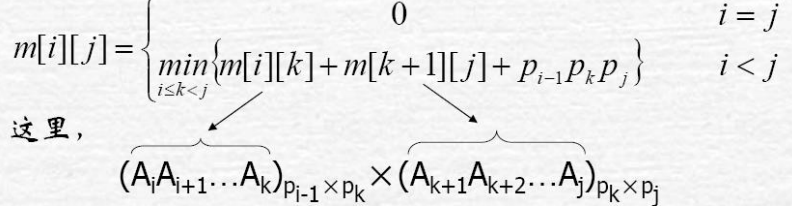
其中，
① 取得的𝑘为𝐴[𝑖:𝑗]最优次序中的断开位置，并记录到表𝑠[𝑖][𝑗]中，即𝑠[𝑖][𝑗] ← 𝑘；
② 𝑚[𝑖][𝑗]实际是子问题最优解的解值，保存下来避免重复计算。

在递归计算时，许多子问题被重复计算多次。这也是该问题可用动态规划算法求解的又一显著特征。

步骤3：计算最优代价，自底向上记忆化方式求解𝒎 [𝒊] [𝒋]

用动态规划算法解此问题，可依据其递归式以自底向上的方式进行计算。在计算过程中，保存已解决的子问题答案。每个子问题只计算一次，而在后面需要时只要简单查一下，从而避免大量的重复计算，最终得到多项式时间的算法。

void MatrixChain(int *p，int n，int **m，int **s)
{for (int i = 1; i <= n; i++) m[i][i] = 0;for (int r = 2; r <= n; r++)for (int i = 1; i <= n - r+1; i++) {int j=i+r-1;m[i][j] = m[i+1][j]+ p[i-1]*p[i]*p[j];s[i][j] = i;for (int k = i+1; k < j; k++) {int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];if (t < m[i][j]) { m[i][j] = t; s[i][j] = k;}}}
}
时间复杂度分析：
①算法matrixChain的主要计算量取决于算法中对𝑟, 𝑖和𝑘的3重循环；
②循环体内的计算量为𝑂(1)，而3重循环的总次数为$𝑂(𝑛^3)$；
③因此算法的计算时间上界为$𝑂(𝑛^3)$；
④算法所占用的空间显然为$𝑂(𝑛^2)$。

计算实例

假设有如下矩阵

1. 令m[i][i]均为0。
2. 以此计算m[i][i+1],m[i][I+2]……
3. 绘制表格

过程如下所示：