数据库的索引概述与常见索引结构
目录
1. 数据库索引概览
1.1. 索引的作用
1.2. 索引的分类
2. 索引的数据结构
2.1. 索引的数据结构评价
2.2. B树
2.3. B+树
2.4. Hash索引
1. 数据库索引概览

1.1. 索引的作用
索引的作用:
类似书籍目录,帮助数据库快速定位目标行,避免全表扫描。
何时不应该建索引:
1. 数据量少
表中行数 < 1,000 时,额外索引带来的 I/O 开销可能超过收益。
2. 高基数(重复度高)字段
如性别(男/女)在普通分布下:若需筛选 50% 或更多行,索引查找 + 回表成本高于直接全表扫描。
3. 频繁写操作的字段
索引需要维护,INSERT/UPDATE/DELETE 代价较高。
选用索引时的权衡:
利(提升查询效率):大幅加速海量数据检索。
弊(维护索引所需的代价):
- 占用额外存储空间。
- 降低数据库写操作性能。
- 索引选择器耗时(过多索引会增加优化器判断成本)。
1.2. 索引的分类
1. 按功能逻辑:
| 类型 | 约束 | 用途 |
| 普通索引 | 无 | 提升查询效率 |
| 唯一索引 | UNIQUE | 保证字段值唯一 |
| 主键索引 | UNIQUE + NOT NULL | 标识行、默认聚集索引 |
| 全文索引 | — | 支持英文全文检索(ES/Solr) |
2. 按物理实现:
| 类型 | 存储方式 | 特点 |
| 聚集索引 | 叶子节点即数据行(按索引列顺序物理排序存储) | 查询高效;每表仅能有 1 个;写入/更新成本较高 |
| 非聚集索引 | 叶子节点存储数据指针,索引与数据分离 | 每表可建多个;查询需“索引→回表”双步;写入/更新成本低于聚集索引 |
3. 按字段个数:
| 分类 | 定义 | 适用场景 | 注意事项 |
| 单列索引 | 只对单个字段建立的索引,如 | 对单字段频繁用于 WHERE 或 ORDER BY 的场景 | 无 |
| 联合索引 (多列索引) | 对多列组合建立的索引,如 | 需要同时过滤或排序多字段,且字段顺序固定的场景 | 必须遵循“最左前缀匹配”原则 |
联合索引与最左匹配原则:
联合索引:多个列组合成一个索引,示例:INDEX (x, y, z)
最左匹配:仅当查询条件中包含索引最左侧列(及其连续子集),索引才会被使用。
能用:WHERE x=…、WHERE x=… AND y=…、WHERE x=… AND y=… AND z=…
失效:WHERE y=… 或 WHERE z=…
2. 索引的数据结构


2.1. 索引的数据结构评价
存储介质对比:
- 内存:读写快、易丢失、容量受限
- 硬盘:持久化、大容量,但 I/O 延迟高
设计目标:
最小化磁盘 I/O 次数 → 直接决定查询速度
评价好坏:
- 树的高度(H):越矮,I/O 次数越少
- 页利用率:每个磁盘块能存多少索引项
- 稳定性:查询深度一致,避免有时深、有时浅
平衡二叉树的不足:
高度 ≈ O(log₂ N) → 对大 N,深度依然较高
每次节点访问都要一次磁盘 I/O
结论:即使自平衡(AVL、红黑树),仍需多次 I/O,不够“矮胖”
2.2. B树
B树的定义:每个节点可有 M (>2)个子节点的平衡搜索树
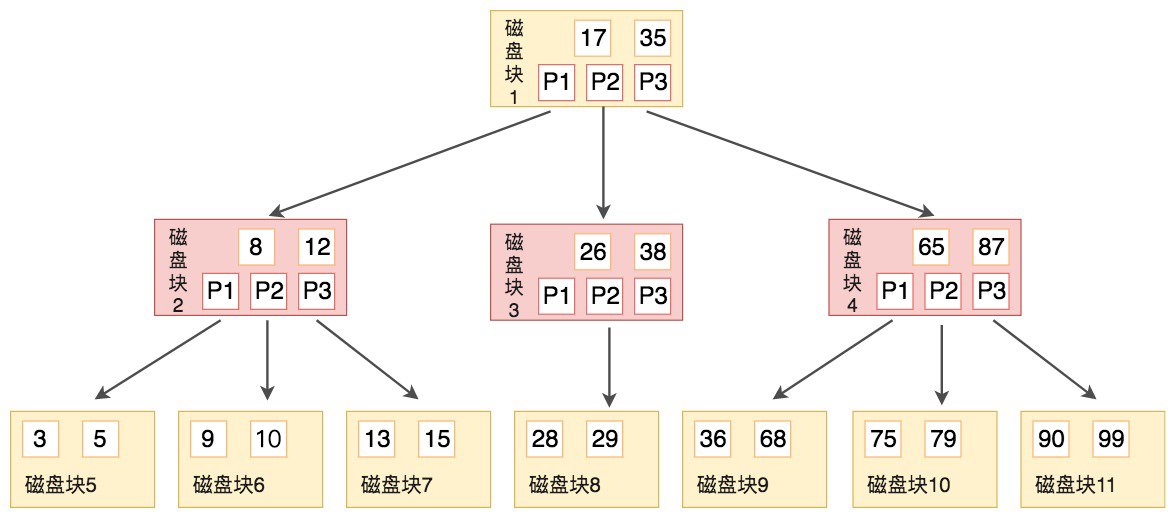
一个 M 阶的 B 树(M>2)有以下的特性:
- 根节点的儿子数的范围是 [2,M]。
- 每个中间节点包含 k-1 个关键字和 k 个孩子,孩子的数量 = 关键字的数量 +1,k 的取值范围为 [ceil(M/2), M]。
- 叶子节点包括 k-1 个关键字(叶子节点没有孩子),k 的取值范围为 [ceil(M/2), M]。
- 假设中间节点节点的关键字为:Key[1], Key[2], …, Key[k-1],且关键字按照升序排序,即 Key[i]<Key[i+1]。此时 k-1 个关键字相当于划分了 k 个范围,也就是对应着 k 个指针,即为:P[1], P[2], …, P[k],其中 P[1] 指向关键字小于 Key[1] 的子树,P[i] 指向关键字属于 (Key[i-1], Key[i]) 的子树,P[k] 指向关键字大于 Key[k-1] 的子树。
- 所有叶子节点位于同一层。
优点:
高度 H ≈ logM N(M 大,H 显著低于二叉树)
每次 I/O 读取一个“页”即一个节点,命中更多关键字
查找流程:
与根节点关键字比较 → 选子指针
逐层定位到叶子 → 找到目标或确认不存在
2.3. B+树
数据库索引常用,例如MySQL使用B+树
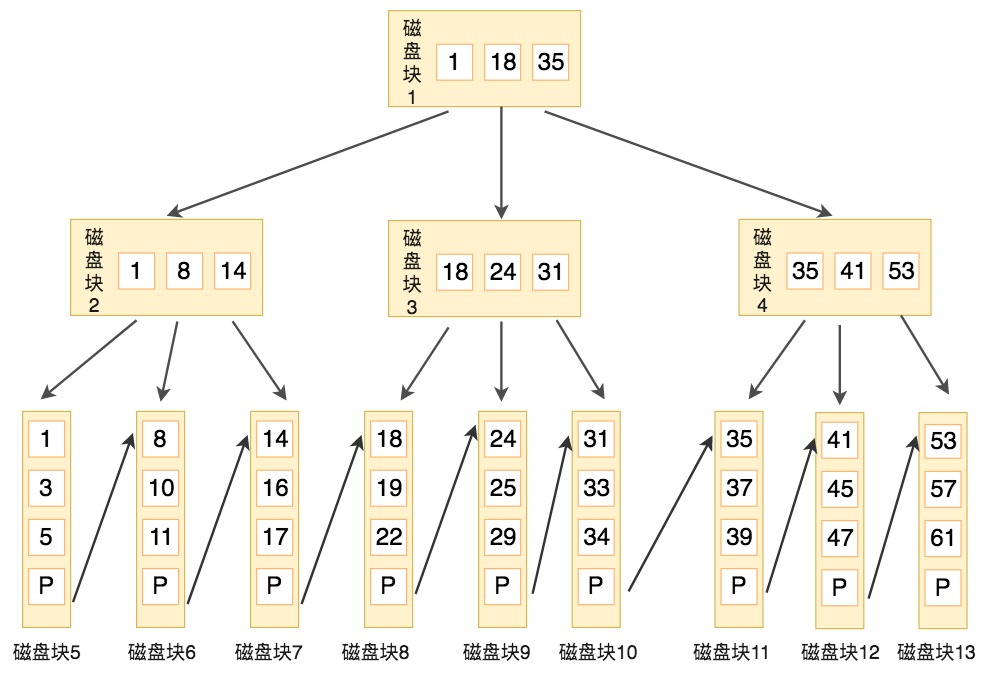
B+ 树和 B 树的特性差异:
- 有 k 个孩子的节点就有 k 个关键字。也就是孩子数量 = 关键字数,而 B 树中,孩子数量 = 关键字数 +1。
- 非叶子节点的关键字也会同时存在在子节点中,并且是在子节点中所有关键字的最大(或最小)。
- 非叶子节点仅用于索引,不保存数据记录,跟记录有关的信息都放在叶子节点中。而 B 树中,非叶子节点既保存索引,也保存数据记录。
- 所有关键字都在叶子节点出现,叶子节点构成一个有序链表,而且叶子节点本身按照关键字的大小从小到大顺序链接。
| 特性 | B Tree | B+ Tree |
| 关键字存放 | 内、叶节点均存;叶子无链表 | 仅叶子节点存,且叶子节点构成有序链表 |
| 指针数量 | k 关键字 → k+1 指针 | k 关键字 → k 指针 |
| 非叶节点作用 | 同时做索引和存储数据 | 仅做索引,数据全在叶子 |
| 树高 | 较高(页内关键字稍少) | 更“矮胖” → 每页关键字更多 → H 更低 |
| 查询稳定性 | 访问到叶或非叶都有可能终止 | 必然访问到叶子,深度一致 |
| 范围查询 | 需中序遍历,成本高 | 利用叶链表直接顺序扫描,最优 |
B+ 树和 B 树的根本的差异在于,B+ 树的中间节点并不直接存储数据。
B+树相较于B树的优势:
1. B+ 树查询效率更稳定。
因为 B+ 树每次只有访问到叶子节点才能找到对应的数据,而在 B 树中,非叶子节点也会存储数据,这样就会造成查询效率不稳定的情况,有时候访问到了非叶子节点就可以找到关键字,而有时需要访问到叶子节点才能找到关键字。
2. 其次,B+ 树的查询效率更高
B+树的每个非叶子节点只存放键,不存放数据,因此相同大小的块可以容纳更多的键,意味着每个节点的分支更多。
分支多(阶越高) → 树的高度更低 → 磁盘IO次数更少 → 查找效率更高。
3. 不仅是对单个关键字的查询上,在查询范围上,B+ 树的效率也比 B 树高。
这是因为所有关键字都出现在 B+ 树的叶子节点中,并通过有序链表进行了链接。而在 B 树中则需要通过中序遍历才能完成查询范围的查找,效率要低很多。
2.4. Hash索引
1. Hash索引的概念
Hash(散列) 是一种将任意长度的输入,通过散列函数转换为固定长度输出的技术。
特性:
- 确定性:相同输入总是产生相同输出。
- 抗碰撞性:不同输入很难产生相同输出。
- 高效比对:可用于快速比较文件是否一致。
2. MySQL中的Hash索引
Hash 索引结构:
- key → Hash 函数 → bucket(桶)
- 桶中保存链表结构,存放指向行记录的指针
- 发生Hash 冲突时在桶中线性查找
优点:
- 查找速度快,适用于等值查询
- 查询过程只需一步定位
缺点:
- 不支持范围查询
- 不支持 ORDER BY 和模糊匹配查询
- 不支持联合索引的最左前缀原则
- 重复值多时效率下降(Hash 冲突)
3. Hash索引与B+树索引对比
| 特性 | Hash 索引 | B+ 树索引 |
| 支持等值查询 | ✅ | ✅ |
| 支持范围查询 | ❌ | ✅ |
| 支持排序优化(ORDER BY) | ❌ | ✅ |
| 支持模糊查询(LIKE) | ❌ | ✅(部分支持) |
| 联合索引支持最左前缀匹配 | ❌ | ✅ |
| 存储顺序 | 无序 | 有序 |
| 重复值多时性能表现 | 性能下降 | 影响较小 |
4. Hash索引的实际应用场景
适用场景:
- 重复值少、需要频繁等值查询的字段
- 临时表、大量 key-value 查询
- Redis 核心结构即基于 Hash 表
MySQL 应用:
- Memory 存储引擎支持显式创建 Hash 索引
- InnoDB 引擎提供自适应 Hash 索引(基于使用频率自动构建)
Hash 是一种高效的数据检索方式,适用于等值查询。
数据库中虽然 B+ 树使用更广泛,但在某些场景下 Hash 更具优势。
选择索引类型需结合实际查询需求。
