小土堆pytorch--损失函数与反向传播
损失函数与反向传播
- 一级目录
- 二级目录
- 三级目录
- 损失函数与反向传播
- 1. 损失函数用法说明
- 1.1 L1LOSS
- 功能
- 公式及参数
- 输入要求
- 已弃用参数
- 形状要求
- 1.2 MSELOSS 
- 功能
- 公式及参数
- 输入要求
- 1.3 交叉熵损失函数
- 功能与原理
- 参数
- 形状要求
- 2. 反向传播
- 概念
- 工作原理
- 直观理解
一级目录
二级目录
三级目录
损失函数与反向传播
1. 损失函数用法说明
我们举个例子,假如一张考试卷满分100分,其中选择30分,填空20分,解答50分
但是某位同学考了30分,这三项都是10分,满分与考试成绩的差距就叫做损失

作用:
- 计算实际输出和目标之间的差距
- 为我们更新输出提供了一定的依据
1.1 L1LOSS
这是pytorch官网对于L1Loss的说明


这是PyTorch中 nn.L1Loss 类的文档说明,用于计算平均绝对误差损失:
功能
度量输入张量 x 和目标张量 y 对应元素间的平均绝对误差(MAE )。
公式及参数
- 未规约情况(
reduction='none') :对每个样本计算损失,公式为 l n = ∣ x n − y n ∣ l_n = |x_n - y_n| ln=∣xn−yn∣ ,得到损失向量 L = { l 1 , . . . , l N } T L = \{l_1, ..., l_N\}^T L={l1,...,lN}T , N N N 是批量大小。 - 规约情况 :
reduction='mean'(默认 ):对损失向量求均值,计算所有元素损失平均值。reduction='sum':对损失向量求和,得到所有元素损失总和。
输入要求
x 和 y 是形状任意但需相同、元素总数相同的张量,支持实值和复值输入。
已弃用参数
size_average 和 reduce 已弃用,指定它们会覆盖 reduction 参数设置,推荐使用 reduction 来确定损失规约方式。
形状要求
输入和目标张量形状为 (N, *) ,N 是批量大小, * 代表任意额外维度;若 reduction='none' ,输出形状与输入相同,否则输出为标量。
import torch
from torch.nn import L1Lossinputs = torch.tensor([1,2,3], dtype = torch.float32)
targets = torch.tensor([1,2,5], dtype = torch.float32)inputs = torch.reshape(inputs,(1,1,1,3))
targets = torch.reshape(targets, (1,1,1,3))loss = L1Loss()
result = loss(inputs, targets)print(result)
运行结果为

import torch
from torch.nn import L1Lossinputs = torch.tensor([1,2,3], dtype = torch.float32)
targets = torch.tensor([1,2,5], dtype = torch.float32)inputs = torch.reshape(inputs,(1,1,1,3))
targets = torch.reshape(targets, (1,1,1,3))loss = L1Loss(reduction="sum")
result = loss(inputs, targets)print(result)
换成sum的模式,就是求损失的和了

1.2 MSELOSS 
这是关于PyTorch中 nn.MSELoss 类的说明,用于计算均方误差损失:
功能
衡量输入张量 x 和目标张量 y 对应元素间的均方误差(即L2范数的平方 )。
公式及参数
- 未规约情况(
reduction='none') :对每个样本计算损失,公式为 l n = ( x n − y n ) 2 l_n = (x_n - y_n)^2 ln=(xn−yn)2 ,得到损失向量 L = { l 1 , . . . , l N } T L = \{l_1, ..., l_N\}^T L={l1,...,lN}T , N N N 是批量大小。 - 规约情况 :
reduction='mean'(默认 ):对损失向量求均值,即计算所有元素损失的平均值。reduction='sum':对损失向量求和,得到所有元素损失总和。
输入要求
x 和 y 是形状任意的张量,且元素总数相同。
import torch
from torch.nn import L1Loss, MSELossinputs = torch.tensor([1,2,3], dtype = torch.float32)
targets = torch.tensor([1,2,5], dtype = torch.float32)inputs = torch.reshape(inputs,(1,1,1,3))
targets = torch.reshape(targets, (1,1,1,3))loss = L1Loss(reduction="sum")
result = loss(inputs, targets)print(result)loss = MSELoss(reduction="sum")
result = loss(inputs, targets)print(result)
运行结果

1.3 交叉熵损失函数


一般用于多分类问题

这是PyTorch中 nn.CrossEntropyLoss 类的相关说明,用于分类问题损失计算:
功能与原理
- 将
LogSoftmax和NLLLoss融合在一个类中,适用于C个类别的分类训练任务。输入是每个类别的原始未归一化分数,目标是类别索引。 - 计算公式:未指定权重时, l o s s ( x , c l a s s ) = − l o g ( e x p ( x [ c l a s s ] ) ∑ j e x p ( x [ j ] ) ) = − x [ c l a s s ] + l o g ( ∑ j e x p ( x [ j ] ) ) loss(x, class) = -log(\frac{exp(x[class])}{\sum_{j} exp(x[j])}) = -x[class] + log(\sum_{j} exp(x[j])) loss(x,class)=−log(∑jexp(x[j])exp(x[class]))=−x[class]+log(∑jexp(x[j])) ;指定权重
weight时, l o s s ( x , c l a s s ) = w e i g h t [ c l a s s ] ( − x [ c l a s s ] + l o g ( ∑ j e x p ( x [ j ] ) ) ) loss(x, class) = weight[class](-x[class] + log(\sum_{j} exp(x[j]))) loss(x,class)=weight[class](−x[class]+log(∑jexp(x[j]))) ,最后对小批量样本损失进行平均或求和。
参数
- weight (可选):手动为每个类指定重缩放权重,是大小为C(类别数)的1D张量,处理训练集类别不均衡时有用。
- size_average 、reduce :已弃用,分别涉及损失平均或求和相关功能,指定它们会覆盖
reduction。 - ignore_index (可选):指定被忽略的目标值,其不参与输入梯度计算,
size_average=True时,损失在非忽略目标上平均。 - reduction (可选):确定输出的规约方式,
'none'不规约,'mean'求加权均值(默认 ),'sum'求和。
形状要求
- 输入:形状为
(N, C)或(N, C, d1, d2, ..., dk)( K ≥ 1 K\geq1 K≥1 ,用于高维情况),N是批量大小,C是分类的类别数。 - 目标:形状为
(N)或(N, d1, d2, ..., dk)( K ≥ 1 K\geq1 K≥1 ),值在0到C - 1范围。 - 输出:
reduction='none'时与目标形状相同,否则为标量。

import torch
from torch import nn
from torch.nn import L1Loss, MSELoss# inputs = torch.tensor([1,2,3], dtype = torch.float32)
# targets = torch.tensor([1,2,5], dtype = torch.float32)
#
# inputs = torch.reshape(inputs,(1,1,1,3))
# targets = torch.reshape(targets, (1,1,1,3))
#
# loss = L1Loss(reduction="sum")
# result = loss(inputs, targets)
#
# print(result)
#
# loss = MSELoss(reduction="sum")
# result = loss(inputs, targets)
#
# print(result)x = torch.tensor([0.1,0.2,0.3])
y = torch.tensor([1])
x = torch.reshape(x, (1,3))
loss_cross = nn.CrossEntropyLoss()
result = loss_cross(x, y)
print(result)
总结一下:
- loss function 要根据需求(要解决的问题)来使用
- 要注意输入输出
2. 反向传播
概念
反向传播(Backpropagation)是一种在神经网络训练中计算梯度的方法 。神经网络训练的目标是调整参数(权重和偏置 ),使网络输出尽可能接近真实标签,而反向传播能高效计算参数的梯度,基于梯度来调整参数。
工作原理
- 前向传播:输入数据进入神经网络,依次经过各个隐藏层,最后到达输出层得到输出结果。比如图像识别任务中,图像数据输入,经多层处理得到各类别的预测概率。
- 计算损失:用损失函数(如前面介绍的交叉熵损失等 )衡量预测结果和真实标签的差距。损失反映了当前网络预测的好坏程度。
- 反向传播:从输出层开始,将损失关于输出的梯度反向传播回网络的输入层。依据链式法则,计算损失对每一层参数(权重和偏置 )的梯度。例如在一个简单的两层神经网络中,先算出损失对第二层参数的梯度,再通过链式法则算出对第一层参数的梯度 。
- 参数更新:根据计算出的梯度,使用优化算法(如随机梯度下降 )来更新神经网络的参数。梯度指示了参数调整的方向和幅度,通常沿着梯度反方向调整参数,使损失降低。
直观理解
可以把神经网络想象成一个复杂的函数,输入数据经函数运算得到输出。反向传播就像是告诉这个函数,它哪里算得不对,通过计算梯度指出参数如何调整能让计算结果更准确,然后不断调整参数,让函数计算得越来越好。
import torchvision
from torch import nn
from torch.nn import Sequential, Conv2d, MaxPool2d, Flatten, Linear
from torch.utils.data import DataLoaderdataset = torchvision.datasets.CIFAR10("das",train=False,transform=torchvision.transforms.ToTensor(),download=True)
dataloader = DataLoader(dataset, batch_size=64)class Test(nn.Module):def __init__(self):super(Test,self).__init__()self.model1 = Sequential(Conv2d(3,32,5,padding=2),MaxPool2d(2),Conv2d(32, 32, 5, padding=2),MaxPool2d(2),Conv2d(32, 64, 5, padding=2),MaxPool2d(2),Flatten(),Linear(1024, 64),Linear(64, 10))def forward(self,x):x = self.model1(x)return xloss = nn.CrossEntropyLoss()
test = Test()
for data in dataloader:imgs, targets = dataoutputs = test(imgs)result_loss = loss(outputs,targets)# print(result_loss)result_loss.backward()print("ok")

可以看到往下走了一行是,自动更新出梯度的参数
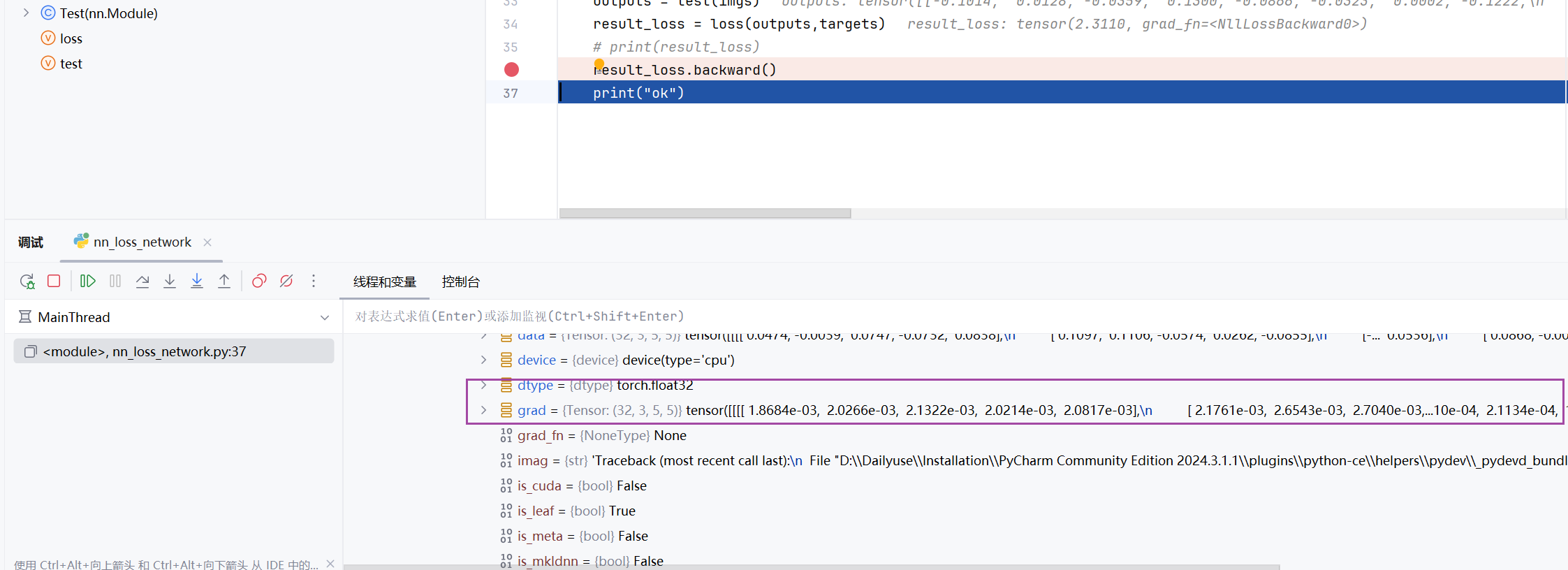
下一节我们会使用优化算法(如随机梯度下降 )来更新神经网络的参数
