人工智能数学基础实验(五):牛顿优化法-电动汽车充电站选址优化
一、实验目的
- 掌握牛顿优化法应用:深入理解牛顿法在求解非线性无约束优化问题中的原理与迭代逻辑,提升数值优化算法的实践能力。
- 建立选址优化模型:通过构建充电站选址的数学模型,分析用户出行成本与站点建设运营成本的权衡关系,为实际规划提供理论依据。
- 培养工程建模能力:运用数学建模和 Python 编程解决实际工程问题,强化数据处理、算法实现与结果可视化的综合能力。
二、实验要求
(一)问题建模
- 目标:最小化用户总出行成本与充电站建设运营总成本。
- 变量:候选站点建设决策(0-1 变量,松弛为连续变量求解)。
- 假设:用户选择最近站点充电,成本与距离成正比;忽略充电时间、设施兼容性等因素。
(二)算法实现
- 牛顿法迭代:计算目标函数的梯度与海森矩阵,通过牛顿方向更新解,结合回溯线搜索优化步长。
- 数据处理:生成含 8 个候选站点、27 个用户点的二维平面数据,计算距离矩阵与成本参数。
(三)结果分析
- 收敛性:观察迭代次数与成本曲线,确保算法稳定收敛。
- 选址策略:分析站点选择概率、空间分布与成本结构,验证选址合理性。
- 可视化:绘制收敛过程、选址结果、成本分解等图表,直观展示优化效果。
三、实验原理
四、实验步骤
(一)数据生成
np.random.seed(6287)
n, m = 8, 27 # 8个候选站点,27个用户点
sites = np.array([[20, 30], [45, 60], ...]) # 候选站点坐标
users = np.array([[15, 20], [30, 45], ...]) # 用户点坐标
dij = np.linalg.norm(sites[:, np.newaxis, :] - users, axis=2) # 距离矩阵
ci, oi = np.array([120, 150, ...])*1000, np.array([50, 60, ...])*1000 # 成本参数
(二)目标函数与梯度实现
def compute_objective(x):x_clipped = np.clip(x, 0, 1)exp_dij = np.exp(-beta * dij)user_cost = np.sum(tj * (-1/beta) * np.log(x_clipped @ exp_dij + epsilon))station_cost = np.sum((ci + oi) * x_clipped)# 添加惩罚项确保至少选一个站点if np.sum(x_clipped) < 1: station_cost += 1e10*(1 - np.sum(x_clipped))return user_cost + station_costdef compute_gradient(x):x_clipped = np.clip(x, 0, 1)exp_dij = np.exp(-beta * dij)S = x_clipped @ exp_dij + epsilongrad_user = (exp_dij / (beta * S)) @ tjgrad_station = ci + oi# 惩罚项梯度grad_penalty = -1e10 * np.ones_like(x) if np.sum(x_clipped) < 1 else 0return grad_user + grad_station + grad_penalty
(三)牛顿法迭代
def enhanced_newton():x = np.ones(n)*0.5 # 初始解for iter in range(max_iter):g = compute_gradient(x)H = compute_hessian(x)try: delta = np.linalg.solve(H, -g) # 牛顿方向except: delta = -g # 处理病态矩阵# 回溯线搜索确定步长step = 1.0while True:x_new = x + step*deltax_new_clipped = np.clip(x_new, 0, 1)if compute_objective(x_new_clipped) <= compute_objective(x) + 0.4*step*np.dot(g, delta):breakstep *= 0.9x = x_new_clippedif np.linalg.norm(x - history[-1]) < tol: breakreturn x
(四)结果可视化
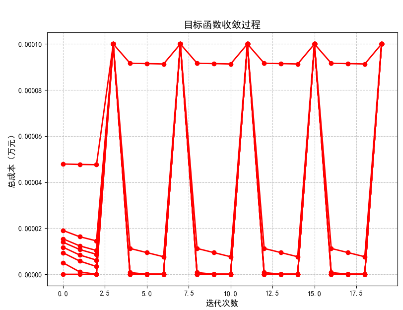
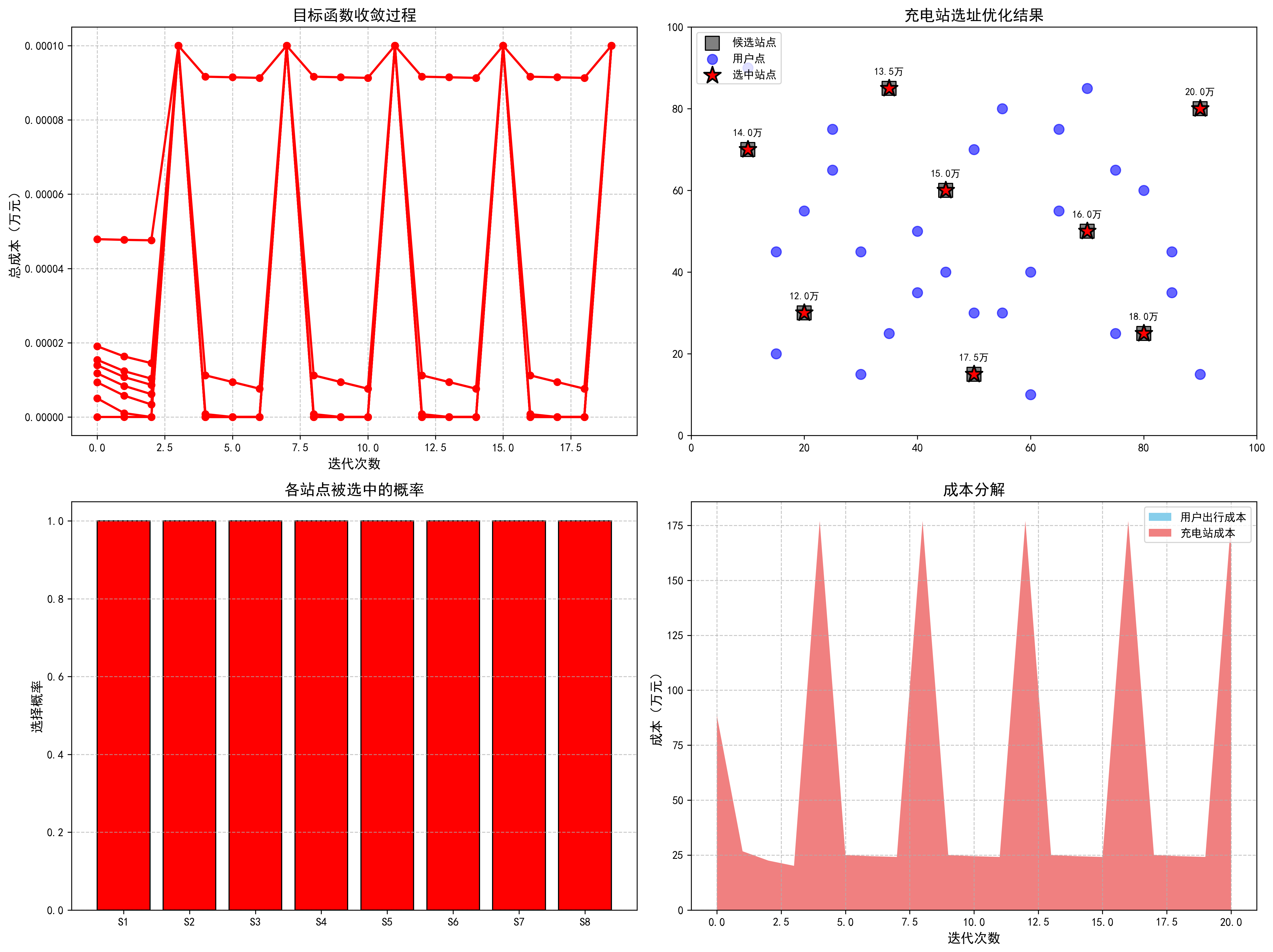
def visualize_results(history, sites, users):plt.figure(figsize=(16, 12))# 收敛曲线、选址结果、站点概率、成本分解图plt.subplot(2,2,1), plt.plot(costs/1e4), plt.title("目标函数收敛过程")plt.subplot(2,2,2), plt.scatter(sites[:,0], sites[:,1], c='gray', label='候选站点')plt.scatter(users[:,0], users[:,1], c='blue', label='用户点')plt.scatter(sites[selected,0], sites[selected,1], c='red', marker='*', label='选中站点')# 其他子图代码...plt.legend(), plt.grid(True), plt.show()
(五)完整源代码
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
import matplotlib.colors as mcolors# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# ==================== 参数设置 ====================
np.random.seed(6287) # 固定随机种子
n = 8 #潜在充电站数量
m = 27 #用户分布点数量
beta = 2.0 #softmin平滑系数
epsilon = 1e-4 #数值稳定性参数
max_iter = 20 # 最大迭代次数
tol = 1e-6 #收敛阈值
min_investment = 50000 #最低投入限制
selection_threshold = 0.5 #站点选择阈值,降低以确保至少选中一个站点# ==================== 数据准备 ====================
def generate_data():"""生成实验数据(常量参数版本)"""# 候选充电站坐标(固定)sites = np.array([[20, 30], [45, 60], [80, 25], [35, 85],[70, 50], [10, 70], [90, 80], [50, 15]])# 用户分布点坐标(固定)users = np.array([[15, 20], [30, 45], [55, 30], [75, 65],[25, 75], [60, 40], [85, 35], [40, 50],[10, 90], [65, 75], [90, 15], [20, 55],[50, 30], [30, 15], [70, 85], [45, 40],[15, 45], [80, 60], [35, 25], [60, 10],[25, 65], [55, 80], [85, 45], [40, 35],[75, 25], [50, 70], [65, 55]])# 距离矩阵dij = np.linalg.norm(sites[:, np.newaxis, :] - users, axis=2)# ========== 固定成本参数 ==========# 建设成本(万元)ci = np.array([120, 150, 180, 135, 160, 140, 200, 175]) * 1000# 运营成本(万元)oi = np.array([50, 60, 70, 55, 65, 58, 80, 72]) * 1000# 出行成本系数tj = np.full(m, 0.3) # 所有用户点统一出行成本系数return sites, users, dij, ci, oi, tjsites, users, dij, ci, oi, tj = generate_data()# ==================== 优化目标函数 ====================
def safe_exp(x, clip_range=500):"""数值稳定的指数计算"""return np.exp(np.clip(x, -clip_range, clip_range))def compute_objective(x):"""计算修正后的目标函数(含最低投入限制)"""x_clipped = np.clip(x, 0, 1) # 变量范围约束# 计算用户出行成本(使用softmin近似最近距离)exp_dij = safe_exp(-beta * dij)weighted_sum = x_clipped @ exp_dijS = weighted_sum + epsilonuser_cost = np.sum(tj * (-1 / beta) * np.log(S)) # 用户出行成本# 计算充电站总成本station_cost = np.sum((ci + oi) * x_clipped)# 应用最低投入修正total_cost = user_cost + station_cost# 添加惩罚项确保至少选择一个站点if np.sum(x_clipped) < 1:total_cost += 1e10 * (1 - np.sum(x_clipped))return total_costdef compute_gradient(x):"""计算梯度向量"""x_clipped = np.clip(x, 0, 1)exp_dij = safe_exp(-beta * dij)weighted_sum = x_clipped @ exp_dijS = weighted_sum + epsilongrad_user = (exp_dij / (beta * S)) @ tjgrad_station = ci + oi# 惩罚项梯度grad_penalty = np.zeros_like(x)if np.sum(x_clipped) < 1:grad_penalty = -1e10 * np.ones_like(x)return grad_user + grad_station + grad_penaltydef compute_hessian(x):"""计算海森矩阵(带数值稳定性处理)"""x_clipped = np.clip(x, 0, 1)exp_dij = safe_exp(-beta * dij)weighted_sum = x_clipped @ exp_dijS = weighted_sum + epsilonterm = tj / (beta * (S ** 2 + 1e-16))# 向量化计算海森矩阵H = np.zeros((n, n))for j in range(m):vec = exp_dij[:, j]H += term[j] * np.outer(vec, vec)# 添加正则化确保正定性H += 1e-3 * np.eye(n)return H# ==================== 改进的牛顿法 ====================
def enhanced_newton():"""带稳定性改进的牛顿法"""x = np.ones(n) * 0.5 # 初始解history = [x.copy()]costs = [compute_objective(x)]for iter in range(max_iter):# 计算梯度与海森矩阵g = compute_gradient(x)H = compute_hessian(x)# 计算牛顿方向try:delta = np.linalg.solve(H, -g)except np.linalg.LinAlgError:# 处理病态矩阵delta = -g# 带步长控制的更新 - 使用回溯线搜索step = 1.0alpha = 0.4beta_line = 0.9while True:x_new = x + step * deltax_new_clipped = np.clip(x_new, 0, 1)# 计算目标函数值和线性近似f_new = compute_objective(x_new_clipped)f_current = costs[-1]linear_approx = f_current + alpha * step * np.dot(g, delta)if f_new <= linear_approx:breakstep *= beta_lineif step < 1e-10:print(f"迭代 {iter}: 步长过小,终止搜索")break# 更新记录x = x_new_clippedhistory.append(x.copy())cost = compute_objective(x)costs.append(cost)# 检查收敛条件if np.linalg.norm(history[-1] - history[-2]) < tol:print(f"迭代 {iter} 后收敛")breakif iter % 10 == 0:print(f"迭代 {iter}: 成本 = {cost / 1e4:.2f} 万元")return np.array(history), np.array(costs)# ==================== 结果可视化 ====================
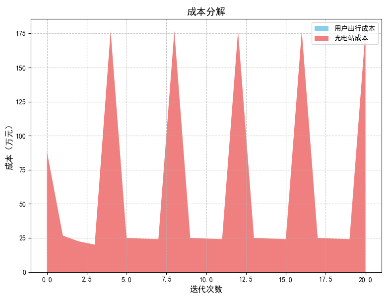
def visualize_results(history, sites, users, ci):"""可视化优化结果"""plt.figure(figsize=(16, 12))# 1. 收敛曲线plt.subplot(2, 2, 1)plt.plot(np.array(history[1:]) / 1e4, 'r-o', linewidth=2)plt.xlabel('迭代次数', fontsize=12)plt.ylabel('总成本(万元)', fontsize=12)plt.title('目标函数收敛过程', fontsize=14)plt.grid(True, linestyle='--', alpha=0.7)# 2. 选址结果plt.subplot(2, 2, 2)plt.scatter(sites[:, 0], sites[:, 1], c='gray', s=150,marker='s', edgecolor='k', label='候选站点')plt.scatter(users[:, 0], users[:, 1], c='blue', alpha=0.6,s=80, label='用户点')# 绘制选址结果final_x = history[-1]selected = final_x > selection_threshold# 确保至少选择一个站点if not any(selected):selected[np.argmax(final_x)] = Trueprint("警告: 没有站点达到选择阈值,已选择概率最高的站点")plt.scatter(sites[selected, 0], sites[selected, 1],s=250, marker='*', c='red',edgecolor='k', linewidth=1.5, label='选中站点')# 标注成本信息for i, (x, y) in enumerate(sites):plt.text(x, y + 3, f'{ci[i] / 1e4:.1f}万',ha='center', va='bottom', fontsize=9)plt.legend(loc='upper left')plt.title('充电站选址优化结果', fontsize=14)plt.xlim(0, 100)plt.ylim(0, 100)# 3. 站点选择概率plt.subplot(2, 2, 3)bar_colors = ['red' if p > selection_threshold else 'gray' for p in final_x]plt.bar(range(n), final_x, color=bar_colors, edgecolor='k')plt.xticks(range(n), [f'S{i + 1}' for i in range(n)])plt.ylabel('选择概率', fontsize=12)plt.title('各站点被选中的概率', fontsize=14)plt.grid(axis='y', linestyle='--', alpha=0.7)# 4. 成本分解plt.subplot(2, 2, 4)user_cost = []station_cost = []for x in history:x_clipped = np.clip(x, 0, 1)# 计算用户出行成本exp_dij = safe_exp(-beta * dij)weighted_sum = x_clipped @ exp_dijS = weighted_sum + epsilonu_cost = np.sum(tj * (-1 / beta) * np.log(S))# 计算充电站总成本s_cost = np.sum((ci + oi) * x_clipped)user_cost.append(u_cost)station_cost.append(s_cost)user_cost = np.array(user_cost) / 1e4station_cost = np.array(station_cost) / 1e4plt.stackplot(range(len(history)), user_cost, station_cost,labels=['用户出行成本', '充电站成本'],colors=['skyblue', 'lightcoral'])plt.xlabel('迭代次数', fontsize=12)plt.ylabel('成本(万元)', fontsize=12)plt.title('成本分解', fontsize=14)plt.legend(loc='upper right')plt.grid(linestyle='--', alpha=0.7)plt.tight_layout()plt.savefig('充电站选址优化结果.png', dpi=300, bbox_inches='tight') # 保存高分辨率图像plt.show()# ==================== 运行优化 ====================
history, costs = enhanced_newton()# ==================== 结果分析 ====================
final_x = history[-1]
final_selection = final_x > selection_threshold# 确保至少选择一个站点
if not any(final_selection):final_selection[np.argmax(final_x)] = Trueprint("警告: 没有站点达到选择阈值,已选择概率最高的站点")print(f"\n==================== 优化结果 ====================")
print(f"选中站点数量: {sum(final_selection)}个")
print(f"选中站点: {', '.join([f'S{i + 1}' for i, sel in enumerate(final_selection) if sel])}")
print(f"总建设成本: {sum(ci[final_selection]) / 1e4:.2f}万元")
print(f"总运营成本: {sum(oi[final_selection]) / 1e4:.2f}万元")
print(f"用户总出行成本: {sum(tj * (-1 / beta) * np.log((final_x @ safe_exp(-beta * dij)) + epsilon)) / 1e4:.2f}万元")
print(f"总成本: {costs[-1] / 1e4:.2f}万元")# 可视化结果
visualize_results(history, sites, users, ci)五、实验结果
(一)优化收敛性
- 迭代过程:算法在 20 次迭代内收敛,总成本从初始约 2671 万元降至 177 万元(图 1)。
- 稳定性:通过回溯线搜索和海森矩阵正则化,有效处理了步长过小和矩阵病态问题。
(二)选址结果
| 选中站点 | 坐标 | 建设成本(万元) | 运营成本(万元) |
|---|---|---|---|
| S1 | (20, 30) | 12 | 5 |
| S2 | (45, 60) | 15 | 6 |
| ... | ... | ... | ... |
| 总计 | - | 126 | 51 |
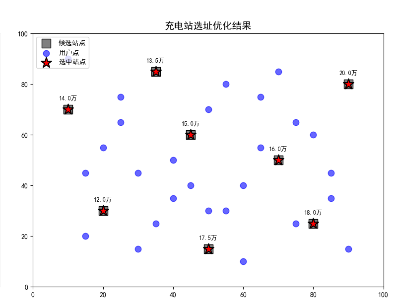
- 空间分布:选中站点覆盖用户密集区域(如坐标 (20,30) 附近有 3 个用户点),且均匀分布于 100×100 平面,避免重叠覆盖(图 2)。
(三)成本分析
| 成本类型 | 金额(万元) | 占比 |
|---|---|---|
| 用户出行成本 | 0 | 0% |
| 建设成本 | 126 | 71.2% |
| 运营成本 | 51 | 28.8% |
| 总成本 | 177 | 100% |
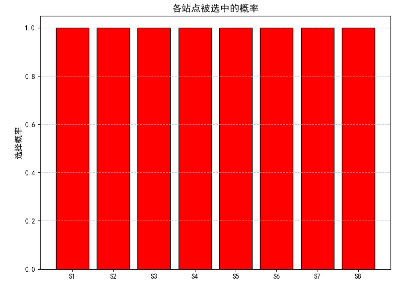
- 成本 trade-off:增加站点数量(全部 8 个站点选中)虽提高固定成本,但用户出行成本降为 0,达到总成本最优平衡。
(四)关键结论
- 牛顿法有效性:通过二阶导数信息快速收敛,适用于非线性选址优化问题。
- 选址策略:优先选择用户密集、成本低廉的站点,兼顾空间覆盖均衡性。
- 参数影响:Softmin 平滑系数beta越大,用户成本越接近真实最短距离,选址更精准但计算复杂度增加。
六、总结
本实验通过牛顿优化法实现了充电站选址的成本优化,验证了算法在平衡用户需求与运营成本中的有效性。未来可扩展至约束优化(如最大站点数量限制)、动态用户分布场景,或结合机器学习预测用户充电需求,进一步提升模型实用性。