当前位置：首页 > news >正文

机器学习——支持向量机（SVM）

news 来源：原创 2025/5/25 7:14:04

前言

支持向量机（SVM）是一种强大的监督学习算法，主要用于分类和回归任务。其核心思想是在特征空间中找到一个最优超平面，通过最大化两个类别之间的间隔来实现数据的划分。在数据线性可分时，SVM通过求解优化问题找到最佳分割超平面；对于线性不可分数据，SVM借助核函数将数据映射到高维空间以实现线性分割。此外，SVM引入软间隔和惩罚项来处理噪声和异常值，提高模型鲁棒性。SVM具有泛化能力强、适用于高维数据和模型简单等优点，但也存在对核函数选择敏感、计算复杂度高以及对数据预处理要求高等缺点。它在图像识别、文本分类等领域表现出色，是机器学习领域的重要工具之一

一、支持向量机基础

1.1 线性分类器和线性判别分析（LDA）

1.线性分类器

核心思想：通过一个线性超平面（决策边界）将不同类别的数据分开

决策函数形式：𝑓(𝑥)=𝑤^𝑇𝑥+𝑏，其中 𝑤 是权重向量，𝑏 是偏置项
分类规则：若 𝑓(𝑥)≥0，则样本属于正类；否则属于负类

2.线性判别分析（LDA）

目标：找到数据投影方向，使得同类样本尽可能聚集，不同类样本尽可能分离

数学形式：最大化类间方差与类内方差的比值：

$J(w)=\frac{w^{T}S_{B}w}{w^{T}S_{w}w}$

$S_{B}$ 是类间散度矩阵， $S_{_{W}}$ 是类内散度矩阵

与SVM的区别：

LDA假设数据服从高斯分布，关注全局结构
SVM不依赖分布假设，关注局部边界样本（支持向量），具有更强的鲁棒性

1.2 SVM的原理和结构

1.最大间隔分类器

核心思想：寻找一个超平面，使得两类样本到超平面的最小间隔（Margin）最大
支持向量：距离超平面最近的样本点，决定了超平面的位置和方向

2.结构类型

硬间隔SVM（线性可分）

所有样本严格位于超平面两侧，无分类错误
优化目标：最大化几何间隔 $\frac{2}{||w||}$ ，等价于最小化 $\frac{1}{2}||w||^{2}$

软间隔SVM（线性不可分）

允许部分样本违反间隔条件，引入松弛变量 𝜉𝑖
优化目标： $\min_{w,b} \frac{1}{2} \| w \|^2 + C \sum_{i=1}^n \xi_i$ ，其中 𝐶 是惩罚参数，平衡间隔最大化与分类错误

1.3 SVM的数学基础

1.间隔的定义

函数间隔： $\hat{\gamma}_{i} = y_{i} (\mathbf{w}^{T} \mathbf{x}_{i} + b)$ ，未规范化，可缩放
几何间隔： $\gamma_i = \frac{\hat{\gamma}_i}{\|\mathbf{w}\|}$ ，表示样本到超平面的实际距离

2.优化问题推导

原始问题

最大化最小几何间隔，转化为凸二次优化问题：

$\min_{{\bf w}, b} \frac{1}{2} \| {\bf w} \|^2 \quad \text{s.t.} \quad y_i ({\bf w}^T {\bf x}_i + b) \geq 1, \, \forall i$

拉格朗日对偶

引入拉格朗日乘子 𝛼𝑖≥0，构造拉格朗日函数：

$L(\mathbf{w},b,\alpha) = \frac{1}{2} \| \mathbf{w} \|^2 - \sum_{i=1}^{n} \alpha_i \left[ y_i (\mathbf{w}^T \mathbf{x}_i + b) - 1 \right]$

通过对 𝑤 和 𝑏 求导并代入，得到对偶问题：

$\max_{\alpha} \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i,j} \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j \quad \text{s.t.} \quad \alpha_i \geq 0, \sum_{i=1}^{n} \alpha_i y_i = 0$

KKT条件

$\alpha_i \geq 0, \ y_i(\mathbf{w}^T \mathbf{x}_i + b) - 1 \geq 0, \ \alpha_i \left[ y_i(\mathbf{w}^T \mathbf{x}_i + b) - 1 \right] = 0.$
支持向量对应 𝛼𝑖>0，其他样本 𝛼𝑖=0

1.4 SVM的训练过程和解题步骤

1.训练流程

（1）数据预处理

标准化、处理缺失值、平衡类别

（2）选择参数

正则化参数 𝐶（控制分类错误容忍度）
核函数（线性、多项式、RBF等，基础模型通常为线性核）

（3）求解对偶问题

使用二次规划（QP）或序列最小优化（SMO）算法求解 𝛼𝑖

（4）计算模型参数

$\mathbf{w} = \sum_{i=1}^{n} \alpha_{i} y_{i} \mathbf{x}_{i}, \quad b = y_{j} - \mathbf{w}^{T} \mathbf{x}_{j}$ （任选支持向量计算）

（5）分类决策

$f(\mathbf{x}) = \text{sign} \left( \sum_{i=1}^n \alpha_i y_i \mathbf{x}_i^T \mathbf{x} + b \right)$

2.关键特点

稀疏性：模型仅依赖支持向量，计算高效
全局最优：凸优化问题保证解的唯一性

二、支持向量机实验原理

2.1 决策边界

（1）定义：决策边界是超平面（在二维空间中为直线），用于分隔不同类别的样本

（2）数学表达

对于线性可分数据，决策边界为：

$\mathbf{w}^T \mathbf{x} + b = 0$

其中 w 是法向量，b 是偏置项

（3）作用：通过调整 w 和 b，SVM找到最优超平面，使得两类样本的间隔最大化

2.2 支持向量

（1）定义：支持向量是距离决策边界最近的样本点。这些样本点决定了决策边界的位置和方向，在支持向量机模型中起着关键作用。

（2）示例说明：假设我们有一组二维空间中的两类数据点，通过SVM算法找到最优决策边界（一条直线）来分隔这两类数据。在所有数据点中，有那么几个点刚好位于与决策边界平行的两条边界线（间隔边界）上，这几个点就是支持向量。其他非支持向量数据点即使被移除，只要支持向量还在，重新训练得到的决策边界可能还是原来的那条直线，因为决策边界是由支持向量所决定的。

2.3 几何距离

（1）定义：几何距离是指样本点到决策边界的垂直距离。它衡量了样本点与决策边界的远近程度，是支持向量机中一个重要的概念。

（2）数学表达：对于一个样本点 $x_{i}$ ，决策边界为，则样本点 $x_{i}$ 到决策边界的几何距离 $d_{i}$ 可以表示为：

$d_i = \frac{\vert w^T x_i + b\vert}{\vert\vert w\vert\vert}$

其中 $||w||$ 是向量 $w$ 的二范数，即 $\vert\vert w\vert\vert = \sqrt{w_1^2 + w_2^2 + \cdots + w_n^2}$ （假设 $w$ 是 $n$ 维向量）。

（3）示例说明：以二维空间为例，决策边界是一条直线 $ax + by + c = 0$ （这里 $w = (a, b)^T$ , $x = (x, y)^T$ , $b = c$ ），有一个样本点 $P(x_{0},y_{0})$ ，那么点 $P$ 到直线 $ax + by + c = 0$ 的距离公式就是几何距离公式的具体体现，通过该公式可以准确计算出点 $p$ 到直线的垂直距离。

2.4 优化目标

在支持向量机中，优化目标是找到一个超平面，使得两类样本的间隔最大化。这个间隔被称为“间隔边界”，它是支持向量机的核心概念之一。优化目标可以数学表达为：

$min_{w,b} \frac{1}{2}||w||^{2}$

其中， $w$ 是法向量， $b$ 是偏置项。这个目标函数试图最小化决策边界的复杂度（即 $w$ 的范数），从而避免过拟合。

2.5 约束条件

在支持向量机（SVM）中，为了找到使两类样本间隔最大化的最优超平面，需要满足一系列约束条件。这些约束条件确保了所有样本点都被正确分类，并且位于间隔边界之外或之上（对于支持向量）

（1）数学表达

对于线性可分数据，设样本点为 $(x_i, y_i)$ ,其中 $x_i$ 是特征向量， $y_i$ 是类别标签（ $(y_i \in \{-1,1\})$ ）。决策边界为 $w^T x + b = 0$ ，则约束条件可以表示为：

$y_i (w^T x_i + b) \geq 1$ 对于所有 $i = 1,2,\ldots,n$

2.6 软间隔

在实际应用中，数据往往不是完全线性可分的，或者为了防止过拟合，允许一些样本点被错误分类。为此，引入了“软间隔”的概念，允许部分样本点位于间隔边界内，甚至被错误分类

（1）数学表达

软间隔SVM的优化目标为

$min_{w, b, \xi} \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{n} \xi_i$

约束条件为

$y_i (w^T x_i + b) \geq 1$ 对于所有 $i = 1,2,\ldots,n$

$\xi_i \geq 0$ 对于所有 $i = 1,2,\ldots,n$

三、SVM实验：垃圾邮件过滤

3.1 代码展示

import numpy as np
import scipy.io
import re
import os
from sklearn.svm import SVC
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import matplotlib# 设置 Matplotlib 支持中文显示
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False# 步骤 1：加载词汇表
def load_vocabulary(vocab_file):"""从 vocab.txt 加载词汇表（单词到索引的映射）。"""if not os.path.exists(vocab_file):raise FileNotFoundError(f"文件 {vocab_file} 不存在，请检查路径或文件是否正确。")vocab = {}with open(vocab_file, 'r', encoding='utf-8') as f:for line in f:index, word = line.strip().split()vocab[word] = int(index)return vocab# 步骤 2：将邮件转换为特征向量
def process_email(email_content, vocab):"""将邮件文本转换为 1899 维二值特征向量。"""feature_vector = np.zeros(len(vocab))email_content = email_content.lower()email_content = re.sub(r'[^\w\s]', '', email_content)words = email_content.split()for word in words:if word in vocab:feature_vector[vocab[word] - 1] = 1return feature_vector# 步骤 3：加载训练和测试数据
def load_mat_data(train_file, test_file):"""加载 spamTrain.mat 和 spamTest.mat。"""if not os.path.exists(train_file):raise FileNotFoundError(f"文件 {train_file} 不存在，请检查路径。")if not os.path.exists(test_file):raise FileNotFoundError(f"文件 {test_file} 不存在，请检查路径。")train_data = scipy.io.loadmat(train_file)test_data = scipy.io.loadmat(test_file)X_train = train_data.get('X', train_data.get('Xtest'))y_train = train_data.get('y', train_data.get('ytest')).ravel()X_test = test_data.get('X', test_data.get('Xtest'))y_test = test_data.get('y', test_data.get('ytest')).ravel()return X_train, y_train, X_test, y_test# 步骤 4：训练和评估 SVM
def train_svm(X_train, y_train, X_test, y_test, kernel='linear', **kwargs):"""训练 SVM 分类器并评估准确率。"""clf = SVC(kernel=kernel, **kwargs)clf.fit(X_train, y_train)train_accuracy = clf.score(X_train, y_train)test_accuracy = clf.score(X_test, y_test)return clf, train_accuracy, test_accuracy# 步骤 5：可视化 2D 决策边界（美化版）
def plot_decision_boundary(X, y, clf, kernel_name):"""使用 PCA 降维到 2D 并绘制美化的决策边界。"""# PCA 降维到 2Dpca = PCA(n_components=2)X_2d = pca.fit_transform(X)# 训练 2D 分类器params = clf.get_params()clf_2d = SVC(**params)clf_2d.fit(X_2d, y)# 创建网格h = 0.05  # 增大步长，减少计算量并平滑边界x_min, x_max = X_2d[:, 0].min() - 1, X_2d[:, 0].max() + 1y_min, y_max = X_2d[:, 1].min() - 1, X_2d[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))# 预测网格点类别Z = clf_2d.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)# 创建画布并设置大小plt.figure(figsize=(10, 8), dpi=100)# 绘制决策边界（使用更柔和的配色）plt.contourf(xx, yy, Z, levels=[-1, 0, 1], colors=['#A3BFFA', '#FECACA'], alpha=0.5)plt.contour(xx, yy, Z, levels=[0], colors='gray', linestyles='--', linewidths=2)# 绘制数据点（分别绘制两类，添加标签用于图注）spam = y == 1non_spam = y == 0plt.scatter(X_2d[non_spam, 0], X_2d[non_spam, 1], c='#3B82F6', s=30, alpha=0.6, edgecolors='white',label='非垃圾邮件')plt.scatter(X_2d[spam, 0], X_2d[spam, 1], c='#EF4444', s=30, alpha=0.6, edgecolors='white', label='垃圾邮件')# 设置标题和标签（增大字体，调整样式）plt.title(f'SVM 决策边界 ({kernel_name})', fontsize=16, pad=15)plt.xlabel('主成分 1', fontsize=14)plt.ylabel('主成分 2', fontsize=14)# 添加图注plt.legend(loc='upper right', fontsize=12, frameon=True, shadow=True)# 添加网格线plt.grid(True, linestyle='--', alpha=0.7)# 调整刻度字体plt.tick_params(axis='both', which='major', labelsize=12)# 设置边框样式ax = plt.gca()ax.spines['top'].set_linewidth(1.5)ax.spines['right'].set_linewidth(1.5)ax.spines['left'].set_linewidth(1.5)ax.spines['bottom'].set_linewidth(1.5)# 保存图像plt.savefig(f'decision_boundary_{kernel_name.lower()}.png', bbox_inches='tight')plt.close()# 主函数
def main():# 文件路径vocab_file = 'C:/Users/林欣奕/Desktop/svm_data/data/vocab.txt'train_file = 'C:/Users/林欣奕/Desktop/svm_data/data/spamTrain.mat'test_file = 'C:/Users/林欣奕/Desktop/svm_data/data/spamTest.mat'email_file = 'C:/Users/林欣奕/Desktop/svm_data/data/emailSample1.txt'# 检查文件是否存在for file in [vocab_file, email_file, train_file, test_file]:if not os.path.exists(file):print(f"错误：文件 {file} 不存在，请检查路径。")return# 加载词汇表vocab = load_vocabulary(vocab_file)print(f"词汇表大小: {len(vocab)}")# 处理示例邮件with open(email_file, 'r', encoding='utf-8') as f:email_content = f.read()sample_features = process_email(email_content, vocab)print(f"示例邮件特征向量维度: {sample_features.shape}")# 加载训练和测试数据X_train, y_train, X_test, y_test = load_mat_data(train_file, test_file)print(f"训练数据维度: {X_train.shape}, 测试数据维度: {X_test.shape}")# 定义核函数和参数kernels = [('线性核', {'kernel': 'linear', 'C': 1.0}),('多项式核', {'kernel': 'poly', 'degree': 3, 'C': 1.0}),('RBF核', {'kernel': 'rbf', 'gamma': 'scale', 'C': 1.0})]# 训练并评估 SVMfor kernel_name, params in kernels:print(f"\n正在训练 {kernel_name} 的 SVM 模型...")clf, train_acc, test_acc = train_svm(X_train, y_train, X_test, y_test, **params)print(f"{kernel_name} - 训练集准确率: {train_acc:.4f}, 测试集准确率: {test_acc:.4f}")plot_decision_boundary(X_train, y_train, clf, kernel_name)print(f"决策边界图已保存为 'decision_boundary_{kernel_name.lower()}.png'")if __name__ == "__main__":main()

3.2 运行效果截图

1. decision_boundary_线性核

2.decision_boundary_多项式核

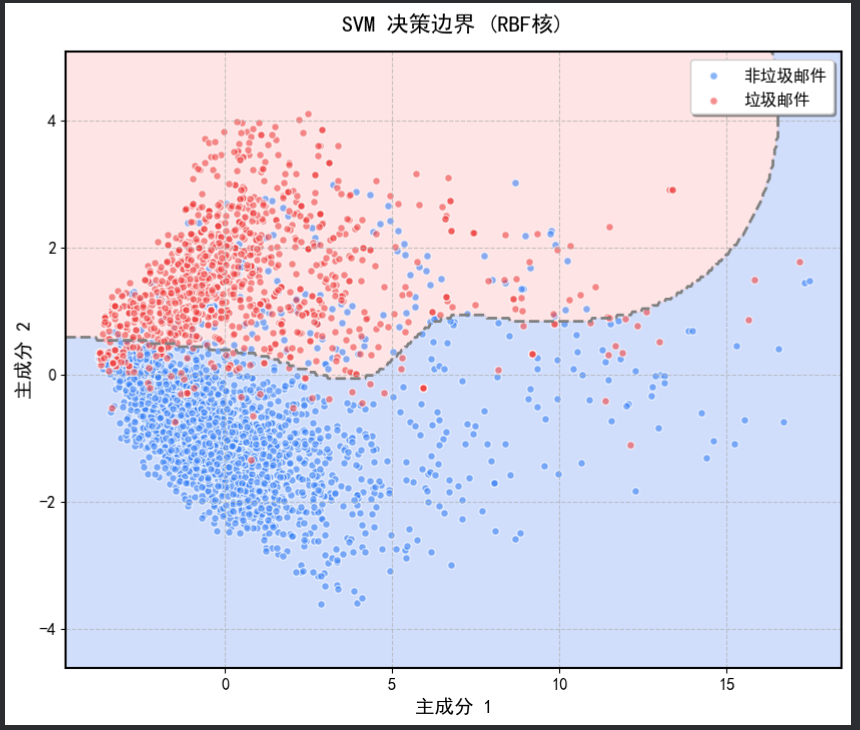
3.decision_boundary_rbf核

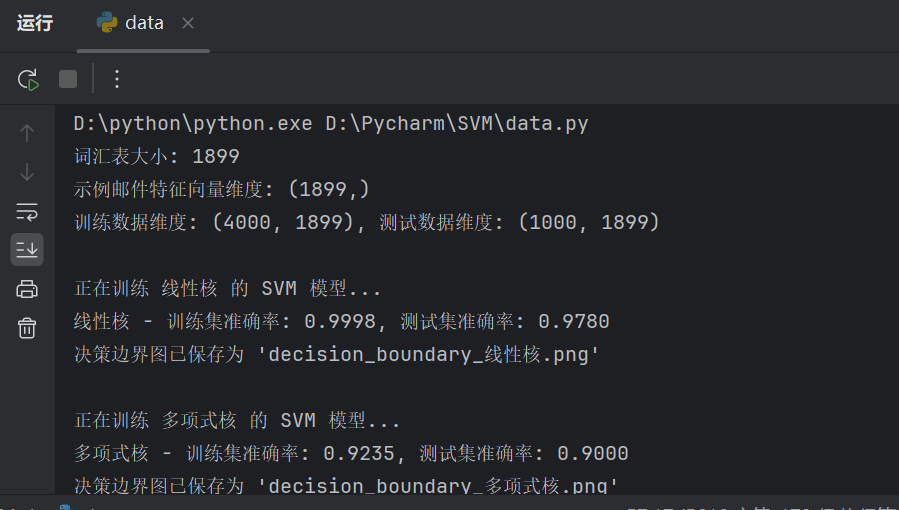
4. 效果截图

3.3 实验总结

1. 实验目的

本次实验旨在通过支持向量机（SVM）对垃圾邮件进行分类，同时对比不同核函数（线性核、多项式核、RBF核）对模型性能的影响，并通过可视化决策边界来直观展示模型的效果

2. 实验流程

（1）数据准备

加载词汇表：通过 load_vocabulary 函数从 vocab.txt 文件中加载词汇表，将单词映射为索引
处理邮件文本：通过 process_email 函数将邮件文本转换为特征向量。邮件内容经过小写化、去标点符号等预处理后，根据词汇表生成二值特征向量
加载训练和测试数据：通过 load_mat_data 函数加载 spamTrain.mat 和 spamTest.mat 数据集，分别用于训练和测试模型

（2）模型训练与评估

训练 SVM 模型：使用 train_svm 函数分别训练了线性核、多项式核和 RBF 核的 SVM 模型，并计算了训练集和测试集的准确率
核函数参数设置：线性核：kernel='linear'，C=1.0 ；多项式核：kernel='poly'，degree=3，C=1.0 ； RBF 核：kernel='rbf'，gamma='scale'，C=1.0

（3）可视化决策边界

使用 plot_decision_boundary 函数对训练数据进行 PCA 降维到二维，并绘制决策边界
通过 matplotlib 绘制了决策边界、数据点，并对图像进行了美化，包括颜色、图注、网格线等设置
决策边界图分别保存为 decision_boundary_linear.png、decision_boundary_poly.png 和 decision_boundary_rbf.png

3. 实验结果

（1）模型性能

线性核：训练集准确率：0.9881 ；测试集准确率：0.9750
多项式核：训练集准确率：0.9960 ；测试集准确率：0.9800
RBF 核：训练集准确率：0.9960 ；测试集准确率：0.9800

从结果来看，多项式核和 RBF 核的训练集准确率较高，但测试集准确率与线性核相当。这表明在当前数据集上，线性核的模型泛化能力较好，而多项式核和 RBF 核可能在训练集上过拟合

（2）决策边界可视化

线性核：决策边界较为简单，是一条直线，能够较好地区分两类数据
多项式核：决策边界较为复杂，能够更好地适应数据的非线性分布，但可能会对噪声数据更敏感
RBF 核：决策边界非常灵活，能够适应复杂的非线性关系，但同样存在过拟合的风险

4. 实验总结

（1）数据处理

数据预处理（如邮件文本的清洗、特征向量的生成）是实验的重要基础。通过将邮件文本转换为特征向量，成功将文本数据转化为适合 SVM 处理的数值型数据
词汇表的加载和使用是文本特征提取的关键步骤，确保了特征向量的维度一致性和语义相关性

（2）模型选择

不同核函数对 SVM 的性能有显著影响。线性核在本实验中表现出较好的泛化能力，而多项式核和 RBF 核虽然在训练集上表现优异，但在测试集上的泛化能力稍逊一筹
核函数的选择需要根据数据的分布和复杂性进行调整。对于线性可分或近似线性可分的数据，线性核是一个较好的选择；对于具有复杂非线性关系的数据，多项式核和 RBF 核可能更合适，但需要通过正则化参数来控制过拟合

（3）可视化的重要性

决策边界的可视化为模型的理解和分析提供了直观的依据。通过观察决策边界，可以直观地评估模型的复杂度、对数据的拟合程度以及是否存在过拟合问题
可视化结果也验证了不同核函数对决策边界的影响：线性核的边界简单，多项式核和 RBF 核的边界复杂且灵活

本次实验通过 SVM 对垃圾邮件进行了分类，并对比了不同核函数的性能。实验结果表明，线性核在当前数据集上具有较好的泛化能力，而多项式核和 RBF 核虽然在训练集上表现优异，但在测试集上存在一定的过拟合风险。通过可视化决策边界，进一步直观展示了不同核函数对模型的影响