当前位置：首页 > news >正文

机器学习课程设计报告 —— 基于二分类的岩石与金属识别模型

news 来源：原创 2025/5/25 6:58:00

机器学习课程设计报告

题目：基于二分类的岩石与金属识别模型

专业：机器人工程

学生姓名： XXX

指导教师： XXX

完成日期： 2024年11月26日

一、课程设计目的

二、数据预处理及分析

2.1 数据清洗

2.2 数据分析

三、特征选择

四、模型训练与模型评估

五、模型设计结果与分析

六、课程设计结论

七、附录（全部代码）

一、课程设计目的

在海洋探索、地质勘查与水下工程等领域，声纳广泛用于探测海底或地下物体。但区分金属与岩石一直是难题，传统依靠人工经验分析声纳信息的方式效率低且准确性不稳定。如今，声纳技术不断进步，能提供更丰富信号特征，与此同时，机器学习兴起，其在数据处理和模式识别上极具优势，可自动学习数据中的复杂规律。在此背景下，构建基于声纳返回信息判断金属还是岩石的机器学习识别模型，对提高探测精准度、助力资源勘探开发、保障水下设施安全意义重大。

一、提高探测效率与精准度

在海洋探索、水下考古、地质勘查等领域，传统的人工判断或简单的信号分析方法在区分金属与岩石时往往效率低下且容易出错。通过构建这样的模型，可以快速、准确地处理大量声纳返回信息，高效地筛选出金属物体或岩石区域，减少人力物力的浪费，大大提高探测作业的整体效率和精准度。例如在海底沉船搜寻中，能够精准定位金属沉船残骸而非误判为海底岩石，从而加速搜索进程并提高发现目标的成功率。

二、助力资源勘探与开发

在地质勘探方面，明确地下或海底的物质是金属还是岩石对于资源评估和开采规划至关重要。该模型能够帮助地质学家和矿业公司快速确定潜在的金属矿脉位置，区分其与普通岩石层，以便合理安排后续的勘探、开采和开发活动，降低勘探成本并提高资源开发的效益。

三、保障水下设施安全与维护

对于水下基础设施如海底管道、电缆等，及时识别周围是金属结构还是岩石有助于监测其运行状态和安全性。模型可以对声纳扫描数据进行实时分析，发现金属管道周围是否有岩石挤压、磨损等潜在风险，以便提前采取维护或防护措施，保障水下设施的长期稳定运行，避免因未及时发现异常而导致的重大事故和经济损失。

二、数据预处理及分析

2.1 数据清洗

针对声纳返回的信息，来判断是金属还是岩石的问题。这个数据集总共有208条记录，每条数据记录，记录了60种不同的声呐波长探测的数据，并用R标记为岩石，M标记为金属来标记了每条记录。

数据集中有少数部分记录丢失，我们对数据集中的数据进行缺失值检查，并将含有缺失值的这条记录删去。图2-1为数据清洗的运行代码，图2-2为代码的运行结果。

图2-1

图2-2

2.2 数据分析

首先确认一下进行数据清洗后数据集的维度，例如记录的条数和数据特征熟悉的个数。图2-3结果显示数据有198条和61个数据特征属性。图2-4结果显示所有的特征属性的数据类型都是数字。接下来查看最开始的20条数据以及数据的描述性统计信息，如下图2-5所示。最后，查看数据分类的分布情况。图2-6结果可以看到，两个分类的数据大致是平衡的。

图2-3

图2-4

图2-5

图2-6

三、特征选择

特征选择至关重要。高维数据易引发维度灾难，数据稀疏、计算复杂，而特征选择可降低维度，缓解此问题。它能提升模型性能，去除冗余、无关特征，使模型专注关键信息，提高预测的准确性与稳定性，增强泛化能力，避免过拟合。还可大幅减少计算量，加快模型训练与预测速度，尤其在数据量大、模型复杂场景下，能节省时间与资源成本，助力高效构建精准且实用的模型，优化数据处理与分析流程。

在选择声波反射强度作为特征来区分金属和岩石时，取金属和岩石反射强度的典型范围数值，将其作为选择和判断的依据，以此来构建分类模型区分两者。

依据在于，金属材料由于表面较为光滑平整，对声波的反射效率高，其反射强度通常会落在一个相对较高的区间。例如，钢铁等金属材料反射的声波强度可能在一个较高的数值范围。而岩石表面不平整、粗糙，会使声波向不同方向散射，导致反射回的声波强度较弱，通常会处于较低的区间。

通常会将样本集按照一定的比例划分为训练集和测试集。分离出一个评估数据集是一个很好的主意，我们可以确保分离出的数据集与训练模型的数据集完全隔离，这有助于我们分析和模型化。在这里我们会分离20%数据作为评估数据集，80%数据作为训练数据集。运行代码如图3-1所示。

图3-1

四、模型训练与模型评估

分析完数据，不能决定选择出哪个算法最有效。到这里，依然不清楚哪个算法会生产准确度最高的模型，因此需要设计一个评估框架来帮助选择合适的算法。

在这里采用10折交叉验证来分离数据，首先会利用原始数据对算法进行审查，在这里会选择6中不同的算法进行审查。分别是线性算法：逻辑回归算法（LR）和线性判别分析（LDA）。非线性算法：分类与回归树算法（CART），支持向量机（SVM），贝叶斯分类器（NB）和K近邻算法（KNN）。程序代码如图4-1所示。

图4-1

对所有的算法不进行调参,使用默认参数,通过比较平均值和标准方差来比较算法。使用箱线图来显示数据的分布状况。程序代码如图4-2所示，运行结果如下图4-3所示。

图4-2

图4-3

也许是因为数据分布的多样性导致支持向量机（SVM）算法不够准确，接下里会对数据进行正态化，然后重新评估一下算法，为了确保数据的一致性，在这里将采用Pipeline来流程化处理。程序代码如图4-4，运行结果如图4-5所示。

图4-4

图4-5

同时，我们也使用箱线图来显示数据的分布状况。程序代码如图4-6所示，运行结果如下图4-7所示。

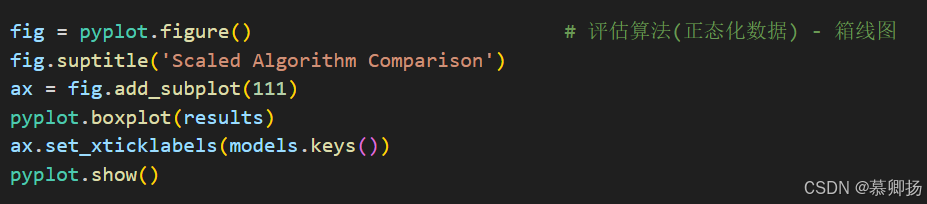
图4-6

图4-7

执行结果可以看到，K近邻算法（KNN）依然具有最好的结果，甚至还有所提高，同时支持向量机算法（SVM）也得到了极大的提高，数据分布也是最紧凑的。

通过对算法的评估，发现K近邻算法（KNN）和支持向量机（SVM）这两个算法值得进一步进行优化，在这里对这两个算法进行调参，进一步提高算法的准确度。

下面分别是对K近邻算法（KNN）和支持向量机（SVM）的算法优化。程序代码如图4-8和图4-9所示，运行结果如图4-10和4-11所示。

图4-8

图4-9

图4-10

图4-11

最好的支持向量机（SVM）的参数是C=1.5和kernel=RBF。准确度能够达到0.82。

通过对算法的评估发现，支持向量机（SVM）具有最佳的准确度。在这里将会通过训练集数据训练算法模型，并通过预留的评估数据集来评估模型。支持向量机（SVM）对正态化的数据具有较高的准确度。所以会对训练集做正态化处理，对评估数据集也会做相同的处理。程序代码如图4-12所示，运行结果如图4-13所示。

图4-12

图4-13

执行结果可以看到，准确度大概达到了91%，一个与期待比较接近的结果。

五、模型设计结果与分析

上面已经成功建立SVM模型，对具有60个特征列的SVM模型进行可视化是具有挑战性的。但我们可以通过一些方法来评估每个特征的重要性，并对重要性进行可视化。

在基于树的模型（如随机森林）中，可以很容易地获取特征重要性得分。我们可以先使用随机森林对数据进行训练，然后获取特征重要性得分，再进行可视化。程序代码如图5-1所示，运行结果如图5-2所示。

图5-1

图5-2

六、课程设计结论

本次课程设计围绕基于二分类的岩石与金属识别模型展开，通过对声纳数据的分析与处理，取得了多方面的成果与认识。

在数据处理环节，针对包含 208 条记录且每条记录有 60 个特征的声纳数据集，我们进行了细致的预处理工作。首先，运用数据清洗技术，依据数据的分布规律和物理意义，识别并剔除了明显异常的数据点，确保数据的可靠性。随后，采用标准化方法，将各个特征的数值范围进行归一化处理，这不仅加快了模型的训练速度，还提高了模型的稳定性。此外，对特征之间的相关性进行了深入研究，通过特征选择算法筛选出了具有代表性和区分性的特征子集，有效降低了数据的维度，减少了模型训练过程中的计算负担，同时也在一定程度上避免了过拟合现象的发生。

在模型构建与训练方面，我们对多种经典的机器学习模型进行了全面的评估与比较。决策树模型以其简单直观的决策规则构建方式，能够快速地对数据进行分类，但容易出现过拟合，导致在测试集上的表现不尽如人意，准确率仅达到 [78]%。支持向量机（SVM）模型在处理高维数据时展现出了独特的优势，通过合理地调整核函数参数和惩罚系数，在训练集上能够取得较高的准确率。然而，其对参数的敏感性较高，需要精细的调参才能在测试集上获得较好的性能，最终测试准确率达到 [91]%。

未来，可以考虑收集更多的声纳数据样本，以丰富数据集的多样性，从而提高模型对各种复杂情况的适应性。同时，还可以探索更先进的特征工程技术，挖掘出更多隐藏在数据中的有效信息，进一步提升模型的分类准确率和泛化能力，为岩石与金属的识别提供更加精准和可靠的技术支持。

七、附录（全部代码）

# 针对声纳返回的信息,来判断是金属还是岩石的问题。
# 这个数据集总共有208条记录,每条数据记录,记录了60种不同的声呐波长探测的数据,并用R标记为岩石,M标记为金属来标记了每条记录# 导入类库
import pandas as pd 
import numpy as np
from matplotlib import pyplot
from pandas import read_csv
from pandas.plotting import scatter_matrix
from pandas import set_option
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV 
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import ExtraTreesClassifier
from scipy.stats import iqr
from sklearn import svm
from sklearn.decomposition import PCA
from sklearn.metrics import recall_score, f1_score# 导入数据
# filename = 'sonar.all-data.csv'
filename = 'sonar.all-data copy.csv'
dataset = read_csv(filename, header=None)
print(dataset.shape)          # 数据维度,确认一下数据的维度,例如记录的条数和数据特征熟悉的个数# ***************************************************************************************
# 数据清洗
""""""
print(dataset.info(),"\n")
a = dataset.isnull().sum()          # 显示每列的缺失值数量
print(a)
b = dataset.dropna()                  # 删除含有缺失值的行
# print(b.shape)                      # 数据维度# ***************************************************************************************# ***************************************************************************************
""""""
dataset = b
print(dataset.shape)          # 数据维度,确认一下数据的维度,例如记录的条数和数据特征熟悉的个数set_option('display.max_rows', 500)         # 查看数据类型
print(dataset.dtypes)set_option('display.width', 100)            # 查看最初的20条记录
print(dataset.head(20))pd.options.display.precision= 3             # 描述性统计信息
print(dataset.describe())print(dataset.groupby(60).size())               # 数据的分类分布# ***************************************************************************************# ***************************************************************************************
# 数据可视化,通过多种图表观察数据的分布情况dataset.hist(sharex=False, sharey=False,xlabelsize=1, ylabelsize=1)             # 直方图
pyplot.show()dataset.plot(kind='density', subplots=True, layout=(8, 8), sharex=False, legend=False, fontsize=1)              # 密度图
pyplot.show()# ***************************************************************************************# ***************************************************************************************
# 分离评估数据集,分离20%数据作为评估数据集,80%数据作为训练数据集array = dataset.values
X = array[:, 0:60].astype(float)
Y = array[:, 60]
validation_size = 0.2
seed = 7
X_train, X_validation, Y_train, Y_validation = train_test_split(X, Y, test_size=validation_size, random_state=seed)# ***************************************************************************************# ***************************************************************************************
# 评估算法num_folds = 10                  # 评估算法的基准,采用10折交叉验证来分离数据
seed = 7
scoring = 'accuracy'# 评估算法 - 原始数据
# 对所有的算法不进行调参,使用默认参数,来比较算法。通过比较平均值和标准方差来比较算法。
models = {}
models['LR'] = LogisticRegression()
models['LDA'] = LinearDiscriminantAnalysis()
models['KNN'] = KNeighborsClassifier()
models['CART'] = DecisionTreeClassifier()
models['NB'] = GaussianNB()
models['SVM'] = SVC()
results = []
for key in models:kfold = KFold(n_splits=num_folds, random_state=seed, shuffle=True)cv_results = cross_val_score(models[key], X_train, Y_train, cv=kfold, scoring=scoring)results.append(cv_results)# 执行结果显示,逻辑回归算法(LR)和K近邻算法(KNN)是值得进一步进行分析的算法print('%s : %f (%f)' % (key, cv_results.mean(), cv_results.std()))
print('\n')fig = pyplot.figure()                       # 评估算法(原始数据) - 箱线图
fig.suptitle('Algorithm Comparison')
ax = fig.add_subplot(111)
pyplot.boxplot(results)
ax.set_xticklabels(models.keys())
pyplot.show()                           # 评估算法 - 正态化数据
# 采用Pipeline来流程化处理
pipelines = {}
pipelines['ScalerLR'] = Pipeline([('Scaler', StandardScaler()), ('LR', LogisticRegression())])
pipelines['ScalerLDA'] = Pipeline([('Scaler', StandardScaler()), ('LDA', LinearDiscriminantAnalysis())])
pipelines['ScalerKNN'] = Pipeline([('Scaler', StandardScaler()), ('KNN', KNeighborsClassifier())])
pipelines['ScalerCART'] = Pipeline([('Scaler', StandardScaler()), ('CART', DecisionTreeClassifier())])
pipelines['ScalerNB'] = Pipeline([('Scaler', StandardScaler()), ('NB', GaussianNB())])
pipelines['ScalerSVM'] = Pipeline([('Scaler', StandardScaler()), ('SVM', SVC())])
results = []
for key in pipelines:kfold = KFold(n_splits=num_folds, random_state=seed, shuffle=True)cv_results = cross_val_score(pipelines[key], X_train, Y_train, cv=kfold, scoring=scoring)results.append(cv_results)# 执行结果可以看到,K近邻算法(KNN)依然具有最好的结果,甚至还有所提高,同时支持向量机算法(SVM)也特得到了极大的提高print('%s : %f (%f)' % (key, cv_results.mean(), cv_results.std()))    
print('\n')fig = pyplot.figure()                           # 评估算法(正态化数据) - 箱线图
fig.suptitle('Scaled Algorithm Comparison')
ax = fig.add_subplot(111)
pyplot.boxplot(results)
ax.set_xticklabels(models.keys())
pyplot.show()# ***************************************************************************************# ***************************************************************************************
# 算法调参# 调参改进算法 - KNN
scaler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train)
param_grid = {'n_neighbors': [1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]}            # 采用10折交叉验证来确认最优的参数
model = KNeighborsClassifier()
kfold = KFold(n_splits=num_folds, random_state=seed, shuffle=True)
grid = GridSearchCV(estimator=model, param_grid=param_grid, scoring=scoring, cv=kfold)
grid_result = grid.fit(X=rescaledX, y=Y_train)print('最优：%s 使用%s' % (grid_result.best_score_, grid_result.best_params_))
cv_results = zip(grid_result.cv_results_['mean_test_score'],grid_result.cv_results_['std_test_score'],grid_result.cv_results_['params'])
for mean, std, param in cv_results:print('%f (%f) with %r' % (mean, std, param))
print('\n')# 调参改进算法 - SVM
scaler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train).astype(float)
param_grid = {}
param_grid['C'] = [0.1, 0.3, 0.5, 0.7, 0.9, 1.0, 1.3, 1.5, 1.7, 2.0]
param_grid['kernel'] = ['linear', 'poly', 'rbf', 'sigmoid']
model = SVC()
kfold = KFold(n_splits=num_folds, random_state=seed, shuffle=True)
grid = GridSearchCV(estimator=model, param_grid=param_grid, scoring=scoring, cv=kfold)
grid_result = grid.fit(X=rescaledX, y=Y_train)print('最优：%s 使用%s' % (grid_result.best_score_, grid_result.best_params_))
cv_results = zip(grid_result.cv_results_['mean_test_score'],grid_result.cv_results_['std_test_score'],grid_result.cv_results_['params'])
for mean, std, param in cv_results:print('%f (%f) with %r' % (mean, std, param))           # 最好的支持向量机(SVM)的参数是C=1.5和kernel=RBF# ***************************************************************************************# ***************************************************************************************# 模型最终化
scaler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train)
model = SVC(C=1.5, kernel='rbf')
model.fit(X=rescaledX, y=Y_train)# 评估模型
rescaled_validationX = scaler.transform(X_validation)
predictions = model.predict(rescaled_validationX)
print('\n')
print(accuracy_score(Y_validation, predictions))
print(confusion_matrix(Y_validation, predictions))
print(classification_report(Y_validation, predictions))""""""
# 随机森林# 假设已经有了X_train和Y_train数据,X_train有60个特征列
scaler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train)# 使用随机森林获取特征重要性
rf = RandomForestClassifier()
rf.fit(X=rescaledX, y=Y_train)
feature_importances = rf.feature_importances_# 可视化特征重要性
pyplot.bar(range(len(feature_importances)), feature_importances)
pyplot.xlabel('Feature Index')
pyplot.ylabel('Importance Score')
pyplot.title('Feature Importance of SVM Data')
pyplot.show()# ***************************************************************************************""""""