当前位置：首页 > news >正文

数字信号处理大实验2 利用FFT估计信号的频率

news 来源：原创 2025/5/24 12:43:24

3.1 实验目的

3.2 实验内容与要求

3.3 实验原理

3.3.1 基于时域求导-频域乘法的n阶导数积分法

3.3.2 基于频域卷积的双/多谱线插值法

3.3.3 基于谱峰和滑动平均的多谱线综合插值方法

3.3.4 基于相邻显著谱线的滑动平均综合插值方法

3.3.5 基于（2）的多步小量时移平均计算法（频域操作）

3.3.6 基于（5）的多步小量频移平均计算法（时域操作）

3.4 实验结果

3.4.1 真实频率估计

3.4.2 探究采样点数N对于估计的相对精度（去量纲化）的影响

3.4.3 探究真实频率对于估计的相对精度的影响

3.4.4 探究初相（采样起始点）对于估计的相对精度的影响

3.4.5 说明、总结与分析

参考文献

3.1 实验目的

了解电磁通信等实际工程中的一些基本问题及解决思路；
培养查阅资料解决问题的能力；
掌握频偏的概念，加深对于DFT、DFT的常用性质（时移/频移等）的理解；
设计具备一定准确性、鲁棒性的算法，估计单频正弦型信号的真实频率；
探究采样率固定时，采样区间长度、起始采样点、被测信号真实频率对于计算精确度和稳定性的影响。

3.2 实验内容与要求

在无噪声干扰条件下，用8000 Hz采样率对某387Hz频率正弦信号进行采样，采集了77个样点作为原始信号。

1、在知网、IEEE网站等查找频率估计方法，利用至少两种频率估计方法编程求给定信号的频率；

2、无噪声、20dB、10dB、5dB、0dB、-5dB，每个信噪比通过至少100次的平均计算，得到频偏的方均根；

3、所有算法使用相同点数的FFT [不大于2048点]；

4、绘出信噪比（对数）-估计均方误差图。

3.3 实验原理

本仿真实验笔者一共实现了6种算法（实际只有5种，不包括（2）），包括：

基于时域求导-频域乘法的n阶导数积分法;
Quinn改进-实部虚部比值与综合权重的双谱线插值法；
基于谱峰和滑动平均的多谱线综合插值方法；
基于相邻显著谱线的滑动平均综合插值方法；
基于（2）的多步小量时移平均计算法（频域操作）；
基于（5）的多步小量频移平均计算法（时域操作）。

3.3.1 基于时域求导-频域乘法的n阶导数积分法

Figure 14 华南理工大学电信学院宁更新老师课件 Chapter5-v3 P28

代码实现

Figure 15 3.3.1 n阶导数-频域范围内求和的代码实现

3.3.2 基于频域卷积的双/多谱线插值法

长度为N点的矩形窗的离散傅里叶变换

对单频f0正弦型信号时域采样，采样序列为y[n]=A*cos(2*π*f0/fs*n+φ)，假定f0/fs是有理数，fs>2*f0；周期为N=m*fs/f0 (∃m，s.t. m*fs/f0∈Z),该信号的DTFT——am=A/2*ejφ, aN-m=A/2*e-jφ,ak=0 for 0<=k<=N-1 and k≠m,N-m

使用N点矩形窗对正弦信号进行截取，需要保证频谱分辨率一致，此时正弦信号的DTFT转化为同样点数的DFT，am和aN-m的序列号和N有关，可能成为小数；频谱为DFT的圆周卷积，对N取余，因此得到的谱线的真实谱峰位置索引经常不是整数，这也是频差δ的来历；

由于实信号幅度频谱的正负频率对称性，算法截取0到pi的频率区间，实际由于双峰卷积造成混叠，从而影响理论插值计算的适用性和准确性。

Figure 16 由于正负频率的对称性造成的混叠，fs在4倍f0附近时双卷积带来的频差计算误差会较小

笔者的算法主要依据为理论插值计算，并在Quinn方法和文献[1]的基础上，通过引入虚部比值和三角函数权重的方式减小频偏估计的误差。截断后信号s的DFT实部虚部分别如下图所示。

Quinn双谱线实部比值插值方法：if δ1≥0 and δ2≥0,δ=δ1;elseif δ1<0 and δ2<0,δ=δ2

基于虚部比值的双谱线插值方法：if δ1≥0 and δ2≥0,δ=δ1;elseif δ1<0 and δ2<0,δ=δ2

Figure 17 公式推导[1]（含笔者的条件修正）、算法流程（部分）[1]

Y(m) 、Y(m-1) 和 Y(m+1) 实部的大小与峰值谱线的相位Φ(m)有关，该算法在峰值谱线的相位Φ(m)接近于0或π时，频率校正精度较高，但当峰值谱线的相位Φ(m)接近于 ±π/2 时，信号频谱分布与FFT系数的关系如图1所示，FFT系数实部序列幅度很小，接近于零，在噪声干扰下，根据实部序列索引的峰值谱线位置容易出错，计算的频偏δ误差也较大，此时频率估计精度较低[1]。

代码实现（部分）

Figure 18 3.3.2算法使用的三角函数综合权重法，角度是幅度谱峰的极角（相位）

3.3.3 基于谱峰和滑动平均的多谱线综合插值方法

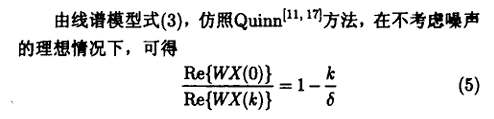
Figure 19 滑动平均原理[2]

根据截断后信号s的DFT表达式，可以推导出幅度谱谱峰和索引距离谱峰索引为k的谱线的实部/虚部比值——Figure18（文献[2]式（5）），在以谱峰索引为中心且左右对称、索引半径为m的区间内，i表示当前的绝对值距离，则从1到m按照3.3.2的方法各可以计算并筛选出一个频偏估计δi ，通过系数乘法配凑进行等权重估计，得到δ。

代码实现（部分）

Figure 20 3.3.3 算法的代码实现（部分）

3.3.4 基于相邻显著谱线的滑动平均综合插值方法

在以谱峰索引为中心且左右对称、索引半径为m的区间内，i表示当前的距离，则从-m到m按照3.3.2的方法各可以计算并筛选出一个频偏估计δi ，通过系数加法配凑进行等权重估计，得到δ。

Figure 21 算法3.3.4 关键代码

3.3.5 基于（2）的多步小量时移平均计算法（频域操作）

在频域对于每一个点的DFT系数乘于ej2kπt0/N,t0是小时移量，本实验设置为一个采样周期（可以是小数倍的采样周期，因为是频域操作）；

这种算法不影响谱峰的位置，但是会影响信号的初相，因此可以一定程度上削减初相对于频偏估计的影响。

Figure 22 算法3.3.5（多步小量时移平均计算法）核心代码

3.3.6 基于（5）的多步小量频移平均计算法（时域操作）

在时域对截断后信号s进行多步小量频移，频移量来自3.3.5算法的频偏估计，通过净频偏存储、多次自迭代计算，理论上频偏量会越来越小，突破阈值后可以视作较准确的估计，如果在给定最大迭代次数内未能突破阈值，使用所有迭代过程中的平均频偏估计值。

Figure 23 算法3.3.6（多步小量时移x多步小量频移）核心代码实现

3.4 实验结果

3.4.1 真实频率估计

Figure 24 截断后信号s，N=77

真实信号频率387Hz，幅度约为2.7, 初相约为137.8°；

采样频率8KHz，频率精度8000/77=103.90Hz。

下面是部分噪声强度配比以及部分算法的估计频率的数值。

未掺杂高斯零均值白噪声：

（1）PMA_ri_comb_interpolation（3.3.3）：324.0058Hz；

（2）Ts_two_p_ri_comb_interpolation (3.3.5):371.8061Hz。

Figure 25 5种算法的准确度和门限测试，门限基本上在10dB左右（N=77，纵坐标为4lg（δRMSE））

在3.4.1的情况中，3.3.5小量时移算法效果最佳，信噪比SNR=30dB时去量纲化真实频偏0.1449。

3.4.2 探究采样点数N对于估计的相对精度（去量纲化）的影响

Figure 26 N=256，纵坐标4lg（δRMSE）- 2，初相、幅度同原信号

Figure 27 N=512，纵坐标4lg（δRMSE）- 2，初相、幅度同原信号

在3.4.2的情况中，3.3.3谱峰滑动平均算法效果最佳，如果把0.5的相对精度（绝对精度8000/256/2=15.625Hz）作为最低合格指标，那么对应到此处的对数坐标是-3.2，N=256、PMA的门限在-5dB左右，N=512、PMA门限在5dB左右；N=256、信噪比SNR=30dB时去量纲化真实频偏0.136；N=512时，信噪比SNR=30dB时小量时移平均计算法精度稍高，去量纲化真实频偏0.111。