机器人收硬币算法c++，完整代码可运行

题目如下：

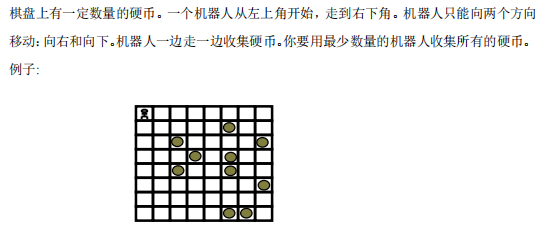
本题要求用贪心算法使得出动最少的机器人来收集场上所有的硬币，首先容易想到的是设计算法使得机器人每次行动都尽可能收集数量最多的硬币，但是实际上此解法并不可行，如以下这种情况:

优先找数量最多的话那么应当是：

以上四种情况，但是实际应当是三种最少，因此优先金币最多是错误的，考虑新的思路。

注意到若两金币其中一个金币在另一个金币的右上方则必须出动两个机器人，如下:

(2, 2)和(3, 3)的机器人是不可能用同一个机器人访问的，因此我们将满足这种关系（一个在另一个的右上角）的硬币分成不同组，这样不同组间的硬币不可能用一个机器人访问到，我们只需要统计总共分为了几组就好。在实际解决中，考虑遍历图中任意两硬币来分组，但是这样要考虑的组合数为Cn2，并且代码结构并不清晰，因此思考别的方式。

我们并不需要考虑任意两点，只需要找到最大组合数就好了，因此完全可以按列来，首先选择第一列的最下面的金币（如果有），我们就看第二列存不存在比第一列y值小的，即右上方的金币，这里同样要找最靠下的。比如第一列y=4,第二列y=2和y=3都有金币，那么我们选择y=3的。重复以上，比如第二列找到y=3的，那么就找第三列存不存在比第二列y值小的，即右上方的金币。这样我们就算出了从第一列开始的不同组的金币组数，那么我们再从第二列开始，直到最后一列，最终计算出整张图的最大不同组的金币组数，即为答案。

接下来我们看代码：
图使用二维数组：

  #include<bits/stdc++.h>
// 机器人收硬币 
using namespace std;vector<vector<int>> arr = {{1, 0, 0, 1, 0, 0},{0, 1, 1, 0, 1, 0},{0, 1, 1, 0, 0, 0},{0, 1, 1, 1, 0, 0},{0, 1, 0, 1, 1, 0}
};
int max_num = 0;
int rows = arr.size();    // 网格的行数
int cols = arr[0].size(); // 网格的列数

然后我们定义核心函数：

int findOne(int x, int y){int i = x+1;int num = 1; // 下一列 while(i < cols){int y_end = -1;for(int j=0;j<rows;j++){if(arr[j][i] == 1 && j < y){y_end = j;}}if(y_end == -1){cout<<i<<"列没有找到"<<endl;}else{cout<<x<<","<<y<<"右上角的坐标已找到"<<i<<","<<y_end<<endl;cout<<"连续斜线的点数量为"<<num+1<<"-------!"<<endl;num++;y = y_end;}// 下一列 i = i+1;}			return num;
} 

这个函数的作用是输入一个节点的坐标，能够计算出从这一列开始的不同组的金币数，我们还是举个例子：

比如从第二列的最后一个点开始(1, 4)，第三列的倒数第二个点是无法用同一个机器人访问的该列的最后一个点，然后算法会从这个点开始(2, 3)，再找出第四列的第一个点（无法用同一个机器人访问的该列的最后一个点）(3,0)，然后第五，六列就没有符合的点了，因此从第二列开始的最大不同组数为 3， 包含第二列能找到三个点。

然后我们主函数内只需要用两个for循环分别找每列的最后一个点即可：

	for(int i=0;i<cols;i++){int y_end = -1;for(int j=0;j<rows;j++){if(arr[j][i] != 0){y_end = j;}}// 找到最后的y，进入函数 if(y_end != -1){cout<<"----------找到了x:"<<i<<" y:"<<y_end<<"的最后一个点，进入循环------"<<endl;int num = findOne(i, y_end);if(num > max_num){max_num = num;}}}

以下是完整代码：

#include<bits/stdc++.h>
// 机器人收硬币 
using namespace std;vector<vector<int>> arr = {{1, 0, 0, 1, 0, 0},{0, 1, 1, 0, 1, 0},{0, 1, 1, 0, 0, 0},{0, 1, 1, 1, 0, 0},{0, 1, 0, 1, 1, 0}
};
int max_num = 0;
int rows = arr.size();    // 网格的行数
int cols = arr[0].size(); // 网格的列数int findOne(int x, int y){int i = x+1;int num = 1; // 下一列 while(i < cols){int y_end = -1;for(int j=0;j<rows;j++){if(arr[j][i] == 1 && j < y){y_end = j;}}if(y_end == -1){cout<<i<<"列没有找到"<<endl;}else{cout<<x<<","<<y<<"右上角的坐标已找到"<<i<<","<<y_end<<endl;cout<<"连续斜线的点数量为"<<num+1<<"-------!"<<endl;num++;y = y_end;}// 下一列 i = i+1;}			return num;
} int main(){for(int i=0;i<cols;i++){int y_end = -1;for(int j=0;j<rows;j++){if(arr[j][i] != 0){y_end = j;}}// 找到最后的y，进入函数 if(y_end != -1){cout<<"----------找到了x:"<<i<<" y:"<<y_end<<"的最后一个点，进入循环------"<<endl;int num = findOne(i, y_end);if(num > max_num){max_num = num;}}}cout<<"至少派出机器人数量为:"<<max_num;return 0;
} 

让我们尝试一个案例：

若是用贪心，每次尽可能最多的收集金币，机器人数量4，但是实际答案应该为三。
算法输出：

end