当前位置：首页 > news >正文

角度回归——八参数检测四边形Gliding Vertex

news 来源：原创 2025/6/8 6:05:02

文章目录

一、介绍
- （一）五参数检测方法（基于角度）
- （二）八参数检测方法（point-based）的边界
二、方案分析
- （一）问题定义
- （二）方案
- （三）Gliding Vertex方案的问题
参考

一、介绍

遥感目标检测Gliding Vertex 是四边形检测器，而且都考虑到了顺序标签点（sequential label points）的问题。我们先给出这两篇文章的链接：

https://arxiv.org/abs/1911.09358

（一）五参数检测方法（基于角度）

在当前常用的旋转检测框的角度定义下，由于存在旋转角度的边界问题，会产生不必要的损失！
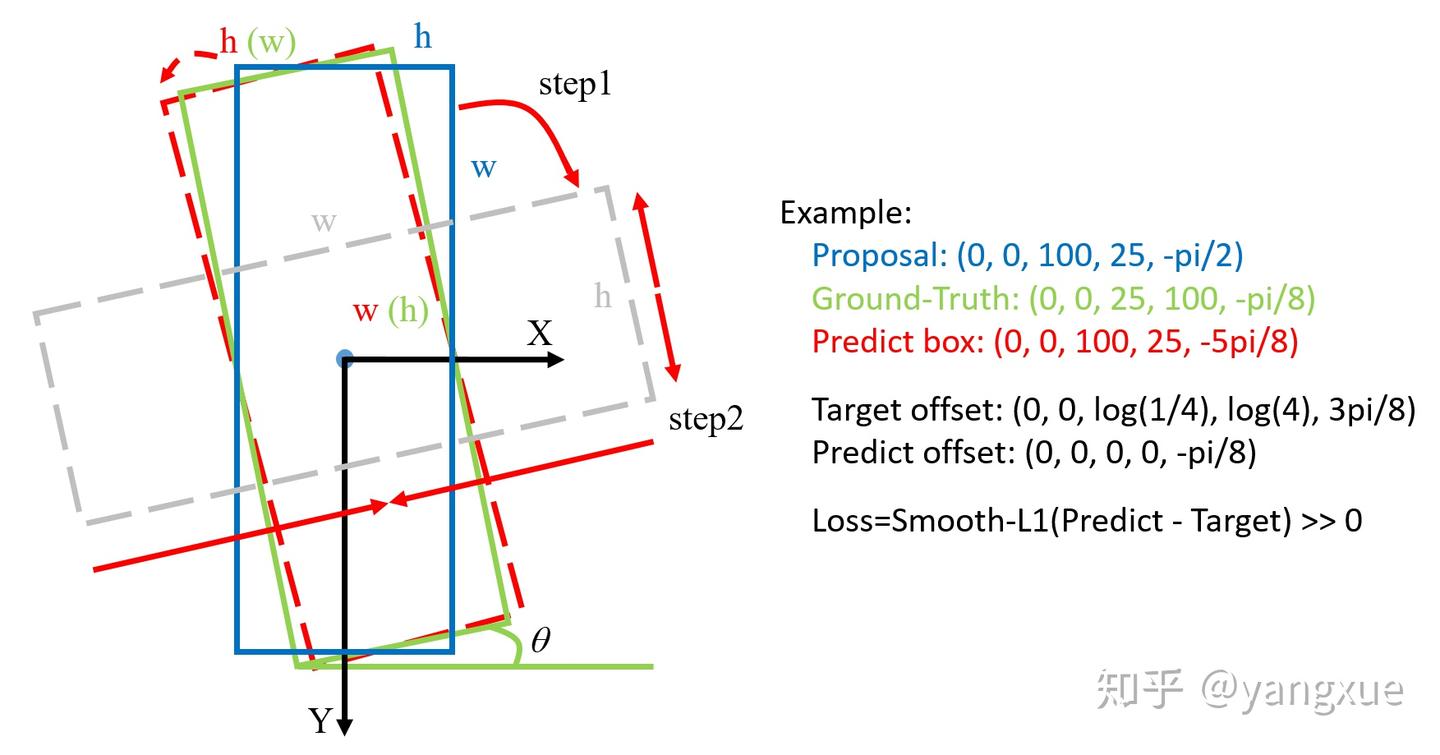
在这里插入图片描述

（二）八参数检测方法（point-based）的边界

如果是蓝框是anchor，红框是ground-truth，那么通过点的排序之后，实际和理想的回归方式是一样的（按照回归的距离定义）
在这里插入图片描述

二、方案分析

（一）问题定义

首先我们要了解一下为什么在做四边形检测前要对四个角点进行排序。举一个简单的例子，如果一个四边形的ground-truth是（x1,y1,x2,y2,x3,y3,x4,y4）并且所有的ground-truth并不是按一定规则顺序标注的，那么检测器有可能给出的预测结果是（x2,y2,x3,y3,x4,y4,x1,y1）。其实这两个是框是完全重合的，但是网络训练算损失的时候并不知道，它会按对应位置计算损失，此时的损失值并不为0甚至很大。

（二）方案

基于上述问题:
1. Gliding Vertex的Head设计
Gliding Vertex文章通过改变框的表示方式避免了排序的麻烦。先检测水平框，这个是没有序列问题的，然后学习水平框四个角点的偏移量来达到四边形检测的目的，其实这里的（偏移量，对应的水平框的点）配对就有排序的意思了。

原文是这样写的：By limiting the offset on the corresponding side of horizontal bounding box, we may facilitate offset learning and also avoid the confusion for sequential label points in directly regressing the four vertices of oriented objects

在这里插入图片描述

Gliding Vertex通过水平框滑动偏移的方式预测旋转框，避免了直接回归无序角点的问题。其head结构包含以下输出分支：

分类分支（Cls Score）：预测目标类别。
水平框回归分支：回归水平外接矩形 $center_x, center_y, w, h)$ 。
偏移比例分支（Alpha）：预测四个角点相对于水平框对应顶点的偏移比例 $(\alpha_1, \alpha_2, \alpha_3, \alpha_4)$ ，通过 $s_i = \alpha_i \cdot w$ 计算实际偏移量。
倾斜因子（Obliquity Factor）：定义为旋转框面积与水平框面积的比值 $\frac{|O|}{|B_h|}$ ，用于区分近水平目标（ $\approx 1$ 时退化为水平框）和倾斜目标。