高等数学-极限

一、函数极限的运算法则及存在准则

例:

1)x->-1*lim[(ln|x+2|)/x(x+1)]=-1

原式=x->-1*lim{(1/x)*[ln(x+2)/(x+1)]}=-1

2)x->0*lim[ln(1+x)]/x=x->0*limln[(1+x)^(1/x)]=ln(x->0*lim[(1+x)^(1/x))]=lne=1

3)x->a*lim[(sinx-sina)/(x-a)]=cosa

4)

5)x->0,y->0*limxsin1/y=0

6)x->0,y->2*lim(sinxy)/x=x->0,y->2*lim[y.(sinxy)/xy]=x->0,y->2limy.x->0,y->2*lim(sinxy)/xy=2

7)x->0,y->0*lim(xy)/(x^2+y^2)不存在

8)x->1,y->0*lim[✅(1+xy)-✅(1-xy]/y=1

9)limn->∞[(√1/n)^n]=1

10)limn->∞{[√1/(n^2)]^n}=1

11)limn->∞(√n)/n-1=limn->∞1/(√n-1/√n)=0

二、两个重要极限

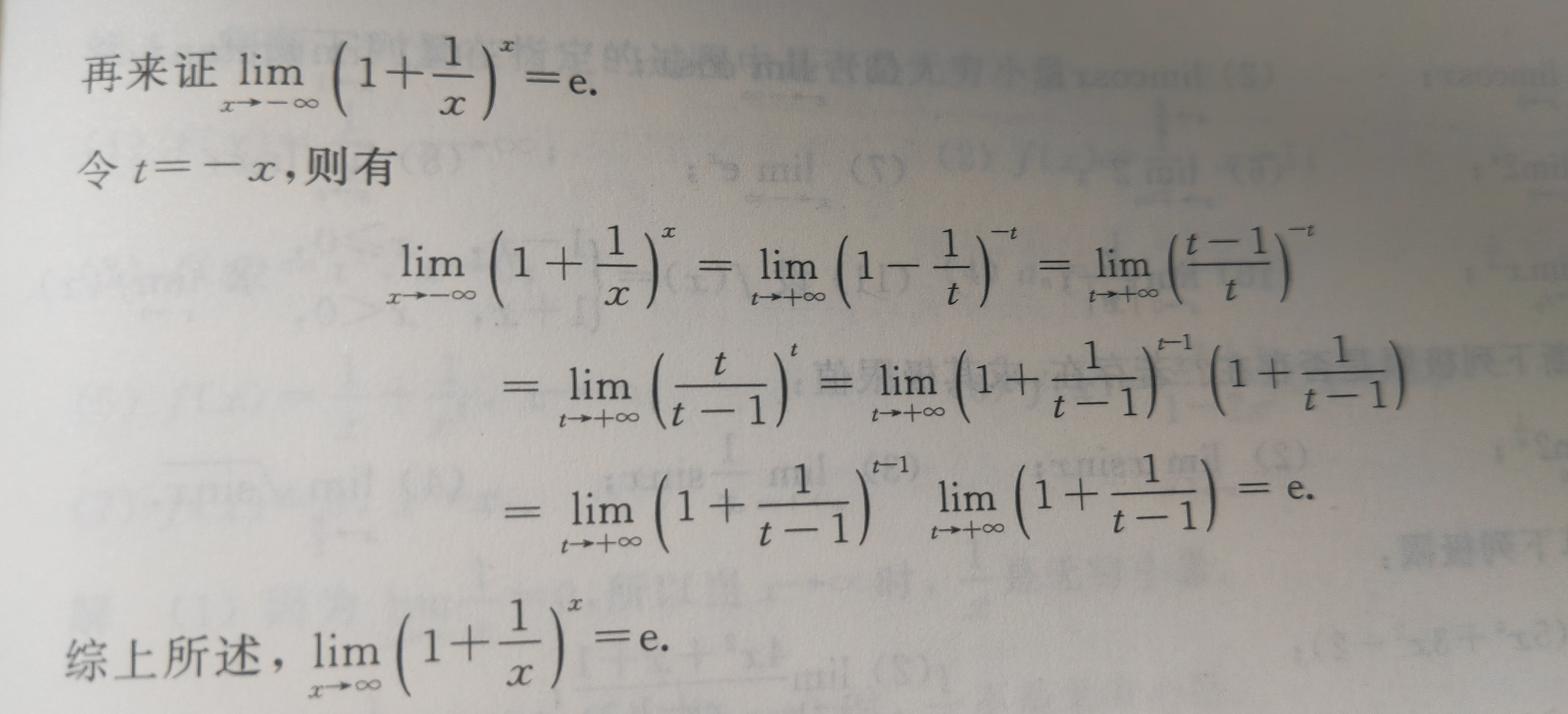注：