采用线性优化改进评估配电网的灵活性范围
1引言
在本文中,柔性一词被定义为“响应外部信号对发电或消耗的修正”。
文章组织结构如下:第二节介绍了代表典型柔性配电网资源技术局限性的线性模型;在第三节中建立了一个线性优化问题;第四节提出了聚合算法;第五节评估所提方法。
2灵活性提供单元(FPUs)建模
在本文中,任何能够为电网提供灵活性的分布式发电机组、存储系统或可控负荷都被定义为灵活性提供单元(FPU)。在文献[7]和[8]中,通过有功和无功灵活性(Pflex和Qflex)限制矩形来表示FPU的灵活性范围。在许多情况下,这种过于简化的表示忽略了有功和无功功率限制的依赖关系(例如功率因数cos(φ)限制或逆变器的技术限制)。为了更好地表达典型电网的运行范围,本文引入了五种线性模型,旨在准确表示每个FPU的PQ灵活性范围。在保持问题是线性的同时,获得更实际的输-配网互连点聚合灵活性范围。该模型旨在根据已知的技术参数,表示相应灵活性的预期技术极限。不管是基于测量值或不同的技术,只要可以用凸多边形表示,就可以集成其他FPU模型。本章定义了五种类型的FPU,如图1所示。

1、类型一
该模型是FPU最简单的表示形式。它可用于表征具有小柔性能力的FPU,以及简化功率逆变器视在功率极限(在二象限和四象限运行模式下)。该模型还代表了存储系统或全变流器风力发电机(PB≥0)。不具备有功功率灵活性的FPU(如:静止同步补偿器)也可以表示为(PA=PB=0)。
2、类型二
具有常数cos(φ)的灵活性模型表示具有有功和无功功率线性相关性的FPUs,例如具有无功补偿的工业负载。
3、类型三
使用具有双象限运行的转子侧转换器(RSC)的双馈异步风力发电机。有功水平较低时,也可能提供无功,但受到逆变器的限制。
4、类型四
光伏通过逆变器调节自身提供的无功。该模型表示符合cos(φ)规范(如VDE 4105)的光伏。在某些情况下,光伏需要通过修改功率因数来帮助维持电网的电压,使用典型值0.9或0.95(ind)。如必要,还能为发电单元建立最小设备运行水平模型。
5、类型五
同步发电机(Synchronous Generator,SG)使用在一些分布式能源中,如小型水电厂。该模型代表了此类发电机运行图的一种近似。同步发电机的视在功率极限和稳定极限都是线性近似的。
3线性最优化模型
文献[7]提出了一个非线性混合整数最优潮流问题,以聚合输-配网互联点(如高压/中压变压器)处配电网的灵活性范围。划定配电网中每个FPU的PQ边界,最终聚合得到一个凸多边形,代表了网络的整体灵活性。图2为该方法的一个示例。交叉点表示FPU和配电网(从电网侧)在给定时刻的期望运行点。优化中考虑了网络约束(即电压和支路流量限制)。聚合的灵活性范围(图2中松弛节点处的面积)考虑了电网状态,仅对应不存在电压越限或线路过载的运行点。

非线性潮流方程准确地描述了电网的状态,但在电网规模较大的情况下,计算代价较高。本文的目标是提供一种使用多个FPU聚合电网灵活性时能减少计算负担的方法。本章介绍了一种线性最优潮流模型,该模型受限于FPU的多边形边界、节点电压限制和线性化的支路潮流限制。目标函数是在PQ笛卡尔平面内对FPU边界多边形在某一特定方向上进行聚合。
3.1潮流节点方程的线性化
极坐标下的潮流方程(节点功率)是非线性的,电压u和角度θ紧密耦合:

节点平衡方程(3)和(4)考虑了连接到节点i上的所有发电机和负载,分为固定部分和柔性部分。固定部分为非柔性电力公司的预期运行点,柔性部分为柔性发电机组(发电机G、负载L和存储系统S)提供的灵活性。FPU提供的有功和无功灵活性作为变量Pflex和Qflex考虑到式(3)和(4)中去:

对于有n个节点和m个FPU的网络,极坐标下的潮流方程需要2n+2m个决策变量(每个母线的u、θ和每个FPU的Pflex、Qflex)。松弛节点的电压保持恒定,幅值为1p.u.,角度为0°。传统的牛顿-拉夫逊潮流(NR-PF)算法使用一阶泰勒展开对网络方程(1)和(2)进行迭代线性化。该算法在每次迭代中通过最小化(3)和(4)中的∆Pi和∆Qi来优化u和θ,直到它们在定义的公差范围内。牛拉法的迭代次数k可以用雅可比矩阵Jk表示为:

在每次迭代中使用u和θ的修正值更新雅可比矩阵Jk,并计算其逆Jk-1(式(5))。调整优化问题的搜索方向,直到达到收敛。牛拉法在定义合理的网络中收敛速度非常快,在大多数情况下只需很少的迭代即可收敛。传统情况下,证明了平起点(u=1 p.u, θ= 0°对所有节点)是一个很好的牛拉法初始猜测。初始猜测越接近网络运行点算法收敛越快。本文利用牛拉法的这一特性对潮流方程进行线性化。线性最优潮流的状态向量x包含变量u、θ、Pflex和Qflex。初始状态向量x0通过给定网络的标准牛拉法得到,其中所有FPU的Pflex和Qflex均置零,从而得到u和θ的初始值。经过k = n次迭代后一旦牛拉法收敛,雅克比矩阵Jx0 = Jn的逆可作为线性模型的线性化常数(式(6))。由此得到的线性网络模型用状态向量x表示为:
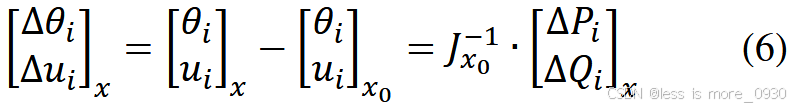
改变Pflex和Qflex的都会直接对u和θ产生影响,导致状态向量x在初始状态向量x0周围漂移。因此,期望在x0附近对网络模型进行线性化的误差小于使用平起点作为线性化点时的误差。
最后,节点电压u的约束为:
![]()
式(1)和(2)通过导纳矩阵Y与网络拓扑直接关联,雅可比矩阵Jx0也与网格拓扑直接关联。操作有载调压变压器根据抽头位置改变导纳矩阵Y,从而改变雅可比矩阵Jx0及其逆。因此,抽头位置不能被视为一个独立的决策变量。对于每个抽头位置,都需要重新计算矩阵导纳矩阵Y和雅可比矩阵Jx0,从而强制为每个抽头位置确定独立的柔性区域。该方法也适用于网格拓扑的更改。
3.2支路潮流限制的线性化
支路流量受到每个支路最大视在功率的限制。这是一个二次方程:

线性最优潮流模型需要线性支路流约束。根据文献[19]和[20],式(8)可以通过n条边的正多边形逼近,而不影响优化问题的数值稳定性。然后用n段Lij,k分段逼近支路的视在功率极限(图3中红色虚线,k =1,…,n)。这意味着每个支路需要n个线性不等式Lij,k。式(9)给出了一个直线方程,定义了如图3所示的每个段Lij,k,其中参数a,b和c取决于角度α和最大支路流量Sij,max。
![]()

连接节点i和j的支路的有功和无功潮流定义为:


式(10)和(11)线性化方法与式(1)和(2)类似,基于用于状态估计问题的扩展雅可比矩阵。Pij和Qij的常数雅可比矩阵由式(10)和(11)的偏导数得到,用由式(6)得到的初始状态向量x0来求值。线性化后的支路潮流方程用状态向量x定义如下:


![]()

得到将支路潮流与状态变量u和θ联系起来的方程组(式(12))。虽然平启动初始化更容易实现,但是在运行点x0周围进行线性化可以提高精度。整合式(9)和(12),得到一个线性不等式系统,该系统约束了每个支路的视在功率Sij(式(13))。这些方程直接依赖于状态变量u和θ:

3.3线性化FPU限制
在前一章中定义了五种不同类型FPU在笛卡尔PQ平面上的灵活性边界。FPU的边界建模为直线,如式(14)所示。这些方程约束了状态变量Pflex和Qflex。参数aflex,i,t、bflex,i,t和cflex,i,t定义凸多边形的段t,定义连接到节点i的每个FPU(图1)。每种FPU类型需要不同数量的线方程,这取决于每个多边形的边数。根据这一定义,得到了FPU的凸线性不等式系统,其形式如下:
![]()
3.4线性约束OPF的定义
采用MATLAB的linprog函数将所提出的线性优化方法表述为最小化问题:

其中向量x包含状态变量u,θ,Pflex和Qflex。参数Aeq和A是矩阵,beq,b,lb和ub是向量。向量fT定义了目标函数,这是PQ笛卡尔平面中的一个线性方程,表示通过松弛节点从分层电网或向分层电网(即通过中压/高压变压器)交换有功和无功功率。该模型假设网络只有一个外部连接,因此只有一个松弛母线[7]。复数支路流Sslack,x = Pslack,x + jQslack,x定义为从松弛母线进入电网的潮流(根据式(12))。网络的灵活性范围由点对(Pslack,x,Qslack,x)定义,使用以下目标函数计算:
![]()
最大化或最小化式(16)可以在PQ笛卡尔平面的定义方向上找到网络聚合柔性范围的不同边界点(Pslack,x,Qslack,x)。参数γ可设置为-1或1,定义了一个最大化或最小化优化问题,而β定义了边界点扫描的方向,允许从网络工作点(Pslack,x0,Qslack,x0)进行360°的勘探。下一章将详细介绍如何通过式(16)获得配电网的总柔性范围。
4配电网灵活性范围估计
确定配电网柔性范围的方法是基于文献[7]中提出的ICPF算法。目标是通过聚合配电网内所有FPU的灵活性范围,确定通过松弛节点进出分层电网的交换潮流的所有可行解决方案的范围。每个解都需要满足所有电网电压和线路负载约束。搜索算法假设一个凸解空间,因为所有的FPU极限都被定义为凸多边形,网格约束也是如此。该算法需要知道每个FPU的技术极限(如图1所示)、连接点以及当前是否在运行。FPU工作点的可观测性质量直接影响网络模型线性化的质量。从网络运行点进行线性化,而不是从平面启动,提高了线性化的质量。还需要对网络拓扑有全面的了解。所提出算法的流程图如图4所示。
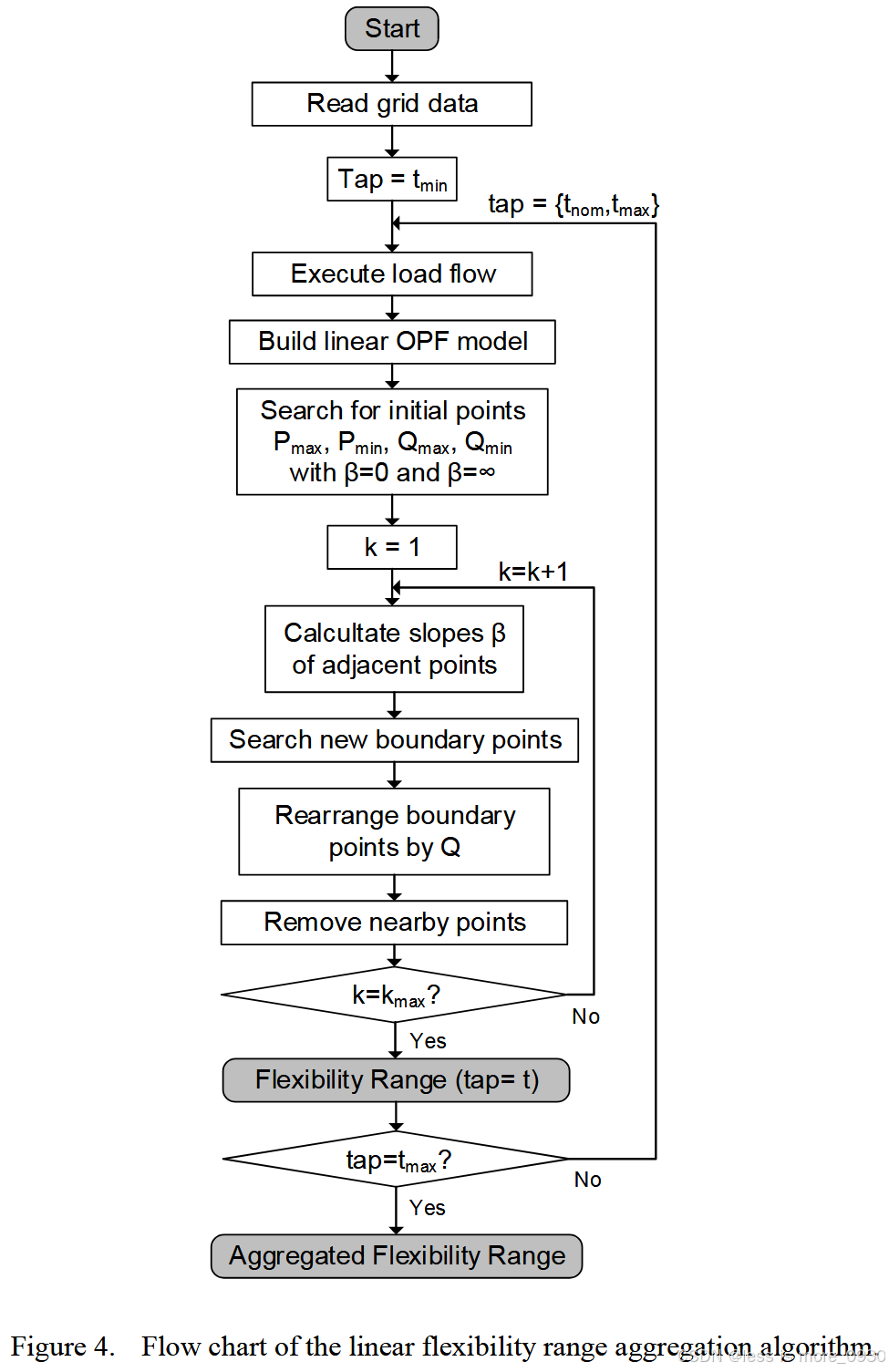
搜索过程从探索极值边界点Pmax,Pmin,Qmax和Qmin开始,通过最小化或最大化式(16),β初始选择为0或∞(图5中的红色点)。连接边界点Pmin-Pmax和Qmin-Qmax的直线相交定义了四个搜索象限(图5中的区域I-IV)。β成为一个变量,定义为连接相邻边界点的直线的斜率(图5中的红色虚线)。在一个象限内,所有β具有相同的符号。表1显示了每个定义象限上变量β的期望符号和在式(16)中使用的参数γ的值。
![]()


在计算了第一组β(图5中的红色虚线)之后,就开始了对象限的迭代探索(图5中的绿色三角形)。所有四个象限都可以独立且并行地进行探索。对于每次迭代,得到的所有象限边界点按照无功值(由高到低)进行重组。在预定义范围ε内,舍弃过于接近的点。随后的迭代使用新的β值重复搜索过程,从新的边界点集计算(例如图5中的蓝色方块)。该过程在kmax迭代后停止。
在文献[7]中,当所有相邻段之间的角度差(φ)小于预定义阈值时,搜索算法收敛。这样可以得到光滑的轮廓,但如果解空间有尖角,算法可能不会收敛。在此工作中,预定义了迭代的最大数量,以便保持恒定的处理时间并禁止不必要的迭代。经过k次迭代,得到最大数量的2k+2个轮廓点(每个象限2k-1)。观察到,k = 3次迭代足以获得聚合灵活性范围(最大25个界点)。得到的轮廓是最后一次迭代后边界点所定义的凸壳(如图5中的蓝线)。
考虑抽头作为一种灵活性,迫使搜索过程独立地重复每个抽头位置。改变抽头位置会直接改变电网的阻抗和电压分布,从而影响电网的无功灵活性(如图6中Q轴之间的聚合灵活性偏移)。电网的聚合灵活性是所有抽头位置的柔性区域的统一。分接开关对有功功率灵活性的影响很小,允许算法仅考虑分接的标称和极端位置进行优化。在一端只需要探索象限I和II,而在另一端则需要探索象限III和IV。标称抽头灵活区域需要确保正确确定有功功率限制。

5算例分析
在本节中,本文提出的方法在德国海德堡的两条20kV城市配电网馈线上进行了验证。网络被标记为网络A(75个节点)和网络B(110个节点)。两者都作为开环运行,并通过110/20 kV 有载调压开关供电(图7)。电网的发电和负载特性详见表2。为了验证算法的有效性,将电网中的每个负载和发电机视为一个FPU。没有可用的存储系统。FPU在电网中的分布情况见表三。



在一台配备i5-6300U 2.4GHz处理器、8GB RAM和64位Windows 10操作系统的笔记本电脑上,使用MATLAB进行仿真。所有节点电压限制设置为0.9 p.u.和1.1 p.u.。仿真考虑有和没有有载调压开关的情况作为灵活性。两个电网上的变压器考虑最大抽头位置为±4%,每步变化1%。支路流动极限(式(13))使用n = 8个线性方程近似。在没有任何并行化搜索过程的情况下,使用“单纯形”求解器对所提出的算法进行了测试。
5.1电网A仿真结果
第一个场景考虑具有高水平自我消耗的中等规模的网络。最大的灵活性是通过削减发电机组和减载来获得的。所有负载允许减少其消耗的最大10%(类型2模型)。结果表明,使用所提出的线性模型获得的柔性面积与使用ICPF非线性模型获得的面积几乎相同,修改后包括定义的FPU模型(图8)。通过NR-PF计算验证了所获得的边界点。线性模型和NR-PF得到的结果在所有点上的平均差值分别为24 kW和67 kVAr(平均相对误差分别为0.31%和5.97%)。选择一个合适的线性化点是非常重要的。与围绕网络运行点x0(图8中红线)进行线性化相比,围绕平面起点(图8中品红色虚线)进行线性化所得到的柔性面积偏差更大。随着边界点Pslack,x与网格运行点Pslack,x0之间的距离增大,线性化误差增大。在这种情况下,虽然ICPF算法被证明是有效的,但所提出的模型产生的结果质量相同,同时减少了80%的计算时间。结果总结于表四。


5.2电网B仿真结果
第二个测试场景考虑了一个更大的网络,其中有大量的FPU(总共130个)。所提出的聚合模型能够提供精确的聚合,与ICPF算法相比,计算时间减少了97.76%。得到的边界点通过NR-PF计算得到确认,显示平均差异为3 kW和31 kVAr(代表平均相对误差分别为0.02%和11.3%)。线性化模型提供的结果质量很好,只要聚合区域保持靠近网络运行点。对于ICPF算法来说,这种情况显示出它的一些局限性,因为算法不能在每个期望的边界点收敛,从而减少了获得的灵活性面积。从图9中可以看出,如果没有正确定位一个边界点,搜索过程可能会错过整个剖面。结果摘要见表四。

6结论
采用牛拉法的雅可比矩阵对潮流方程进行线性化,提出输配网互联点配网有功和无功柔性聚合的线性优化模型。该模型补充了典型FPU的非矩形线性表示,提高了配网聚合精度,且使用的线性规划模型极大的减少了计算时间。同时,在考虑大型电网模型的情况下,保持了潮流计算的准确性,提高了搜索算法的稳定性。
在德国两个不同的包含大量FPU的径向城市配网中测试该算法,用MATLAB中的线性规划工具实现模型。与[7]的ICPF算法相比,计算时间有了显著的提高,而得到的解与非线性模型的偏差很小。在超过100个FPU的情况下,所提出的模型表现出坚韧性,在最大测试网络的情况下,与原始非线性模型相比,只需要不到3%的计算时间,解的质量与非线性模型的差异很小。
该方法具有较强的实际应用价值,提高电网各运营商之间的协调性,帮助评估位于配电网内的输电网运营商激活灵活性的影响(例如用于频率控制目的)。通过将市场结果作为最优潮流模型中的约束,可以观察到灵活性市场的影响。在多个高压水平运行的配电网可以通过从单个馈线获得的聚合结果来表示,因此减少了对敏感电网信息的需求。
参考文献
- Contreras D A, Rudion K. Improved assessment of the flexibility range of distribution grids using linear optimization[C]//2018 Power Systems Computation Conference (PSCC). IEEE, 2018: 1-7.
