Chord Crossing_abc405分析与解答

d先来想想最后什么样的线段是符合条件的，在每一轮询问中，给出a,b两个奇数点，如果线段 i (1<=i<=m)覆盖了a，b的其中一个点，但没有两个点都覆盖，这样的线段i就符合与线段ab相交

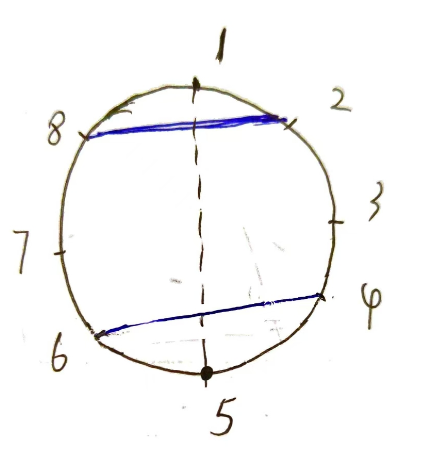
什么是覆盖 ，如下图，线段（4,6）和(2,8)都覆盖了点5，形式化讲，如果线段(a,b) (a<b)和点c，如果a<c且b>c就说线段(a,b)覆盖了点c

如何快速计算有多少个这样的线段 i 呢，如果我们知道给出的m个线段之间的覆盖关系就好了，具体如下，如果线段 j 直接覆盖 线段 i，让节点j当节点i的父亲，如果没有线段直接覆盖线段i，线段i的父亲是节点0

直接覆盖的关系如下：

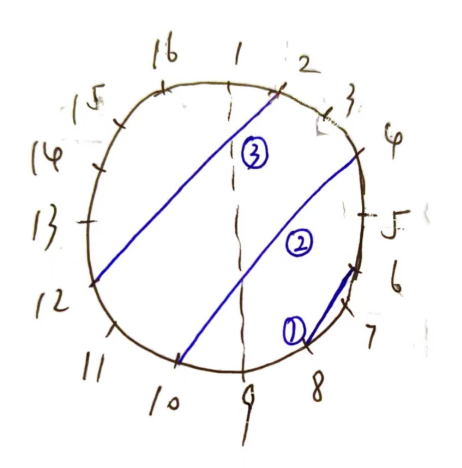
线段2和3都覆盖了1，拿2来说，4<6且10>8 ，所以说2覆盖了1,2是直接覆盖1的，3不是，所以每个线段要么没有其他线段覆盖他，要么直接覆盖的线段唯一，因此我们构建出的是一颗树，这颗树的节点范围是1到m

这颗树有什么用？若在一轮询问中给出点a和b，记直接覆盖点a的线段是a1，直接覆盖点b的线段是b1，（这里，点被线段直接覆盖，关系和线段被线段直接覆盖类似），则树上从a1到b1的路径中除lca(a1,b1)外的节点对应的线段都满足覆盖了a，b中的一个点而没有全部覆盖，如果用倍增法计算出lca(a1,b1)，也知道每个节点的深度，就可以在log(m)时间得到答案：dep[a1]+dep[b1]-2*dep[lca(a1,b1)]

接下来需要解决：
如何得到直接覆盖线段i的线段j，和覆盖点c的线段i，这可以用栈来模拟完成，具体方法见代码

#include<bits/stdc++.h>
using namespace std;
using ll=long long;const ll maxn=1e6+5,maxm=2e5+5;
ll mincov[maxn*2],id[maxn*2],dep[maxm],par[maxm][(ll)log2(maxm)+10];
ll n,m,K;ll lca(ll x,ll y){if(dep[x]<dep[y]) swap(x,y);for(ll i=K;i>=0;i--){if(dep[par[x][i]]>=dep[y]) x=par[x][i];}if(x==y) return x;for(ll i=K;i>=0;i--){if(par[x][i]!=par[y][i]){x=par[x][i];y=par[y][i];}}return par[x][0];
}int main()
{ios::sync_with_stdio(0);cin.tie(0);freopen("D:/in.txt","r",stdin);cin>>n>>m;for(ll i=1;i<=m;i++){ll a,b;cin>>a>>b;id[a]=id[b]=i;}stack<ll> st;st.push(0);for(ll i=1;i<=2*n;i++){if((i&1)==0){  //i是偶数if(id[i]==0) continue;if(st.top()==id[i]){    //出线段st.pop();par[id[i]][0]=st.top();dep[id[i]]=st.size();}else { //入线段st.push(id[i]);}}else {mincov[i]=st.top();}}K=log2(m+5);for(ll i=1;i<=K;i++){for(ll j=1;j<=m;j++){par[j][i]=par[par[j][i-1]][i-1];}}ll q;cin>>q;while(q--){ll a,b;cin>>a>>b;ll x=mincov[a],y=mincov[b];cout<<dep[x]+dep[y]-2*dep[lca(x,y)]<<"\n";}return 0;
}