算法打卡第一天

1.两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。

你可以按任意顺序返回答案示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。
示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]
示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {vector<int> tatal;for(int i = 0; i < nums.size() - 1; i++)//遍历数组{for(int j = i + 1; j < nums.size() ; j++)//从第二个开始防止重和{if(target == nums[i] + nums[j])//target 等于那个数{tatal.push_back(i);tatal.push_back(j);}}}std::cout  << "[";for(int i = 0 ; i <tatal.size(); i++){std::cout <<  tatal[i] << "," << std::endl;}std::cout  << "]";return tatal;}};

2.两数相加

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

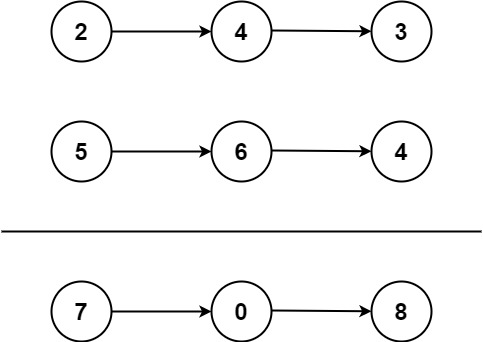
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

提示：

• 每个链表中的节点数在范围 [1, 100] 内
• 0 <= Node.val <= 9
• 题目数据保证列表表示的数字不含前导零

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {//创建一个头节点ListNode head(0);ListNode *current = &head;// 新的进位int carry = 0;//遍历链表while (l1 || l2){//获取当前节点的值 如果为空就是0 int val1 = (l1 != nullptr) ? l1->val : 0;int val2 = (l2 != nullptr) ? l2->val : 0;//    计算当前位的和以及新的进位int sum = val1 + val2 + carry;carry = sum / 10;sum %= 10;// 创建新链表存储 头插current->next = new ListNode{sum};current = current->next;// 移动两个老链表链表指针if (l1){l1 = l1->next;}if (l2){l2 = l2->next;}// 如果最后还有进位，添加一个新节点if(carry > 0){current -> next = new ListNode{carry};}}//返回结果链表的头节点（跳过虚拟头节点）return head.next;}
};

3.无重复字符的最长字串（滑动窗口）

给定一个字符串 s ，请你找出其中不含有重复字符的 最长 子串 的长度。

示例 1:

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

提示：

• 0 <= s.length <= 5 * 104
• s 由英文字母、数字、符号和空格组成

class Solution {
public:int lengthOfLongestSubstring(string s) {// 存储索引和字符unordered_map <char , int> hash_table;int start = 0; //索引的起始位置 也是滑动窗口开始位置int maxLength = 0;  // 长度//遍历字符串for(int end = 0; end < s.size(); ++end)//end是滑动窗口结束位置{//存储当前字符char current = s[end];// 如果字符已存在于哈希表中,且其索引不小于窗口起始位置,则移动窗口起始位置if(hash_table.find(current) != hash_table.end() && hash_table[current] >= start){start = hash_table[current] + 1;}//  更新字符索引hash_table[current] = end;// 更新长度maxLength = max(maxLength,  end - start  + 1);}return maxLength;}
};

4.寻找两个正序数组的中位数（二分查找）

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

思路：

算法的时间复杂度应该为 O(log (m+n)) 二分查找

1.使用分割线吧两个数组分割成两部分**，左右元素个数相等或者线左边元素的个数比右边个数多1个，线左边的所有元素的数值<= 右边的所有元素的数值**，中位数就与红线两侧单词元素有关，确定这条红线的位置使用二分查找

2.线左边的所有元素的数值<= 右边的所有元素的数值意味着第一个数组在分割线左边的最大值小于第二个数组在分割线右边的最小值，第二个数组在分割线左边的最大值小于第一个数组在分割线右边的最小值

分割线应该是这样

分割线应该是这样

可能出现极端的情况

class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {// 算法的时间复杂度应该为 O(log (m+n)) 二分查找  使用分割线吧两个数组分割成两部分，左右元素个数相等或者线左边元素的个数比右边个数多1个，线左边的所有元素的数值<= 右边的所有元素的数值// 确保nums1是小的数组if(nums1.size() >  nums2.size() ){return findMedianSortedArrays(nums2 ,nums1);}//长度int m = nums1.size();int n = nums2.size();// 中间位置 分割线左侧元素数int middle = (m + n + 1) / 2 ;//+1防止单数//在 nums1区间[0,m ]里面查找恰当的分割线// 使得nums[i - 1] <= num2[j] && nums[j - 1] <= nums[i] 这就是第一个数组在分割线左边的最大值小于第二个数组在分割线右边的最小值，第二个数组在分割线左边的最大值小于第一个数组在分割线右边的最小值
//     - 1表示在分割线左边int left = 0;int right = m;while(left < right){int i = left + (right - left + 1) / 2;//left 和right的中间位置 基数int j = middle - i; //分割线在第二个数组左边的元素if(nums1[i - 1] > nums2[j])//分割线在第一个数组左边的元素大于第二个数组在分割线右边的元素// 分割线靠右，分割线应该在i 的左边（无i）{// 下一轮搜索的区间 【left， i- 1】right = i - 1;}else{// 下一轮搜索的区间 【i， right】left = i;}}// 找到nums[i - 1] <= num2[j]int i = left;int j=  middle - i;// 处理一些防止数组越界int numS1LeftMax = (i == 0) ? INT_MIN : nums1[i - 1];int numS1RightMin = (i == m) ? INT_MAX : nums1[i];int numS2LeftMax = (j == 0) ? INT_MIN : nums2[j - 1];int numS2RightMin = (j == n) ? INT_MAX : nums2[j];if((m + n) % 2 == 1)return  std::max(numS1LeftMax, numS2LeftMax);else return (max(numS1LeftMax, numS2LeftMax) + min(numS1RightMin, numS2RightMin)) / 2.0;}
};