操作系统————五种页面置换算法(OPT,FIFO,LRU,NRU,加强版NRU)大总结
❤️❤️❤️算法1:最佳置换算法(OPT)
算法思想:

值得注意的是这是一种理想型算法,实际上并不可能实现,读者需要注意
下面我们来解析一下它的原理:

我们假设有三个内存块,对于页面号引用串,7号,0号,1号这三个页面分配内存块时都存在缺页情况(即原先内存块中并没有这些页面),所以这三个页面会依次被填入三个内存块,然后再给2号页面分配内存块时发现所有内存块都已经被占用,所以就需要替换页面
替换原理:

我们在引用串中往后寻找

可以发现7,0,1这三个页面中,0最先出现,1再出现,7最后出现所以2号页面就替换掉7号页面,进入1号内存块,同理当3号页面需要分配内存块时,此时三个内存块分别被2,0,1号页面占据,我们从3号页面往后的页面串分析,0,2,1号三个页面,0最先出现,2随后出现,1最后出现
所以我们把1号页面替换掉,将3号页面放入内存块3中,后续再有新的页面时我们继续沿用这种方法,从该页面号往后的页面串中寻找最后一个之前出现过的页面替换掉
整个过程中缺页出现了9次,页面替换出现了6次,缺页率我们可以算出是9/20=45%,20是页面串的总长度
注意:缺页未必发生页面置换,若还有空闲的内存块就不用置换
特别提示:

再说一遍:
🍬🍬🍬🍬🍬🍬🍬OPT无法实现!!!!!!!!!!!!!!!!
❤️❤️❤️算法2:先进先出置换算法(FIFO)
算法思想:

实现方法:

注意:每次选择的都是队头页面🍬🍬🍬🍬
我们来看下面的例子:

按照页面访问的顺序,3号页面应该在队头,队列状态如下图:

此时要访问0号页面,所以要替换掉队头的3号页面,把0号页面插到队尾

访问完0号又该3号,此时队头是2号页面,换掉,把3号页面插在队尾,此时队列状态如下:

整个过程中缺页的次数为9次
那么我们再看内存块变为4的情形:

可以发现,当内存块的数量增多时,缺页次数由9次变为了10次,不仅没有减少还增加了,这在操作系统中叫Belady(贝拉迪异常)
🍬🍬🍬Belady异常概念:

FIFO算法缺陷:

注:只有FIFO算法会出现Belady异常🤣🤣🤣🤣
❤️❤️❤️算法3:最近最久未使用置换算法(LRU)
算法思想:

算法实现:

我们来看一个例子:

四个内存块首先分配给最先访问的1,8,7,2号页面,然后访问3号页面时,从3号页面往前的序列串中寻找内存中已经存在的几个页面号,可以发现8最先出现,然后是1,2,7,说明7是最近最久未使用的所以把7号页面替换掉,3号页面放入内存块3,再往后需要重新访问7号页面时,从7号位置往前的序列中看内存中已有的四个页面1,8,3,2哪个最后一个出现,可以看出是8,所以7号页面替换掉8号页面放入内存块2中,得到上图的结果
注意:LRU算法和OPT算法非常相似,两者都是找最后出现的页面,但有如下两个区别
🍬🍬🍬区别1:LRU是从当前访问页面的之前的页面号序列中找的,而OPT算法是从当前访问页面的之后的页面号序列中找的
🍬🍬🍬区别2:OPT算法是正序扫描,LRU算法是倒序扫描
LRU是最最常考的一个算法!!!!!!!
❤️❤️❤️算法4:简单时钟置换算法(CLOCK)
算法思想:

实现方法:

我们来看一个例子:

那么1,3,4,2,5都访问以后访问位都是1,此时需要访问6号页就需要替换

进行第一轮扫描,发现全部为1,先全部置为0

然后开启第二轮扫描,发现1号页访问位是0,替换并把6号页访问位记为1

然后根据序列串该访问3,4号页,都标记为1

访问到7号页面又需要替换,扫描第一个访问位为0的位置,即2号页的位置进行替换并把访问位记为1
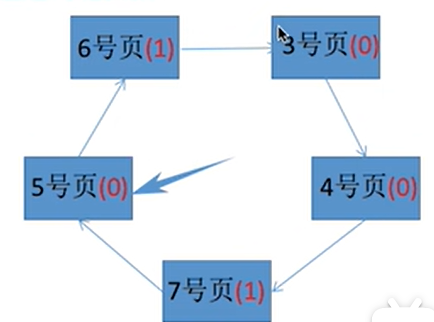
总结:

❤️❤️❤️算法5:加强版时钟置换算法
这是本节最重要的算法
算法思想:

实现方法:

性能分析:

原理精析:
🍬🍬🍬情形1:只扫描一轮**
即第一轮扫描就发现了(0,0)的位置,注意第一轮不修改任何标志位
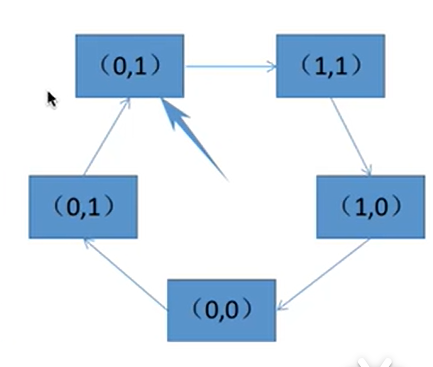
🍬🍬🍬情形2:扫描两轮
第一轮扫描过后发现没有(0,0),第二轮找(0,1)

🍬🍬🍬情形3:扫描三轮
第一轮扫描过后发现没有(0,0),第二轮找(0,1)发现也没有

第二轮扫描过后,笛卡尔坐标的第一位都变成0,因为第二轮是边找边改(没碰到符合的第一位(访问位)就都改为0),得到下图

第三轮再扫描,发现存在(0,0)就找到了合适的位置
🍬🍬🍬情形4:扫描4轮
最坏的一种情况:
第一轮第二轮都没有符合情况的

第二轮结束后,修改为如下情况:

开始第三轮扫描,发现还是没有(0,0),但是第三轮不做修改
继续开始第四轮扫描,发现存在(0,1)进行替换
🍬🍬🍬注意:第一轮和第三轮不做修改只扫描,第二轮扫描完还要修改访问位
我们可以把这种规则总结为下面四个优先级:

最后我们对五种页面置换算法做出总结:

