6.2.5图的基本操作
知识总览:
常考邻接矩阵+邻接表

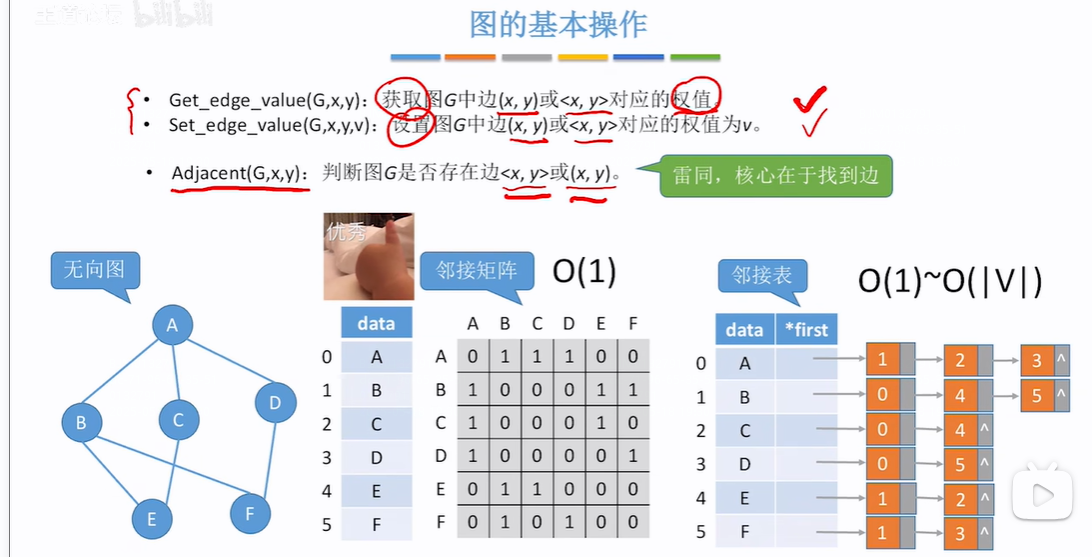
Adjacent判断是否存在边:
无向图:
比如要确定是否存在边<B,D>或(B,D)对于邻接矩阵来说,直接确定B所在行+D所在列对应值是0还是1,0代表无边,1代表有边,即时间复杂度为O(1),对于邻接表来说,要确定B节点下的边节点信息中是否有D节点,即和B节点邻接的最多的边节点有|v-1|个(顶点数-1),即最差情况要遍历|v-1|次,即时间复杂度O(|v-1|)最好情况遍历第一个边节点就找到D节点即时间复杂度O(1)



Neighbours列出图G中与节点x邻接的边:
无向图:
邻接矩阵:遍历x节点所在行和所在列所有值为1的即为邻接的边,要遍历顶点个数数量元素即时间复杂度为O(V)
邻接表:只需遍历这个节点下的边节点,该节点下有几个边节点则要遍历多少次,即最好的时间复杂度为O(1)没边节点或者只有1个边节点,另外就是有v-1个边节点,即O(v)时间复杂度
有向图:
邻接矩阵遍历x节点出边,只需遍历x节点所在行的节点,即数量v,遍历x节点入边,只需遍历x节点所在列节点,即数量v,则时间复杂度为O(v)
邻接表遍历x节点出边,只需遍历该节点下的边节点数量,最好O(1),最坏O(v)遍历x节点入边要遍历所有节点的边节点,看哪些节点下的边节点有x节点,即最坏要遍历顶点O(E)




InsertVertex在图G中插入一个顶点x
邻接矩阵:在保存这些顶点的数组的末尾的空白位置写入顶点x,在邻接矩阵中写入的x的新的行和新的列就可以表示x和其他节点的关系,一般这个关系在邻接矩阵初始化的时候就做好了,所以插入新顶点的开销一般是在写入顶点信息,因为是在数组末尾写入,所以时间开销为O(1)
邻接表:也是在保存这些顶点的数组末尾加上新节点,因为新节点开始没有连任何的边,所以first指针指向为^即null ,因此也是O(1)时间复杂度


DeleteVertex从图中删除顶点x
无向图:
邻接矩阵:删除x顶点之后,要把x节点所在行和所在列的数据都变成0(不实际删除邻接矩阵行列数据),并且把顶点信息中的结构体一维数组加个bool类型的变量,来表示是否是空节点,即在删除x节点之后,把该节点设为1即可,因为只需修改邻接矩阵一行+一列数据,所以只需在O(v)时间完成(实际需要v-1时间+v-1时间,综合2v-2时间,即为O(v)时间,修改结构体因为是数组用O(1)就行,所以综合需要O(v)时间复杂度)
邻接表:删除x顶点之后,要删除x顶点下所有的边节点,还要删除其他节点下的边节点中有x的,最好情况是x顶点没有和其他节点相邻,即只需O(1)时间复杂度,最坏情况,x顶点和其他所有节点相邻,且都放在其他节点的边节点最后一个位置,则需要遍历所有边的信息,即最坏的时间复杂度O(|E|)(听不懂,咋就跟边有关系了??)
有向图:
邻接矩阵和无向图同
邻接表:删除入边,删除x顶点下的所有的边节点,则要看变节点数量,最好没有或只有1个边节点,则时间复杂度O(1),最坏有v-1个边节点,则最坏O(v-1)=O(v),删除入边,则要遍历所有边节点,最坏时间复杂度为O(|E|)



AddEdge增加一条边
无向图:
邻接矩阵:只需O(1)时间复杂度,只需改下邻接矩阵中坐标的值就行吧?
邻接表:如增加C->E边,需要在C节点和E节点的边节点中都增加E、C节点,如果使用头插法,只需O(1)时间复杂度,使用尾插法,就分别遍历C、E节点下所有边节点的数量,只需O(v)时间复杂度
有向图:
邻接矩阵:上同无向图
邻接表:上同无向图



FirstNeighbor找到第一个邻接点
无向图:
邻接矩阵:找到x节点所在行的第一个值为1的节点就是邻接点,最好的情况是第一个节点就是1,即O(1)时间复杂度,最坏情况是最后一个节点是1即要遍历v-1个节点,即O(v)时间复杂度
邻接表:找到x节点下的第一个边节点即为第一个邻接点,即O(1)时间复杂度
有向图:
邻接矩阵:找出边扫描行,找入边扫描列,都是找值为1的节点,即最坏的都为O(v),最好的为O(1),即第一个节点找的就是值为1的节点即为第一个邻接点
邻接表:找出边直接找x节点下的第一个边节点,即时间复杂度为O(1),找入边要遍历所有边的信息,即遍历其他节点下的所有边节点,可能遍历其他边的时候遍历的第一个边的边节点就是x节点,即最好时间复杂度为O(1),最坏是遍历完所有的边节点也没有找到x节点,即最坏时间复杂度为O(|E|)



知识回顾:

未完待续。。。。。。。
