数据结构第七章（四）-B树和B+树

---

B树和B+树

---

还记得我们的二叉排序树BST吗？比如就是下面这个：

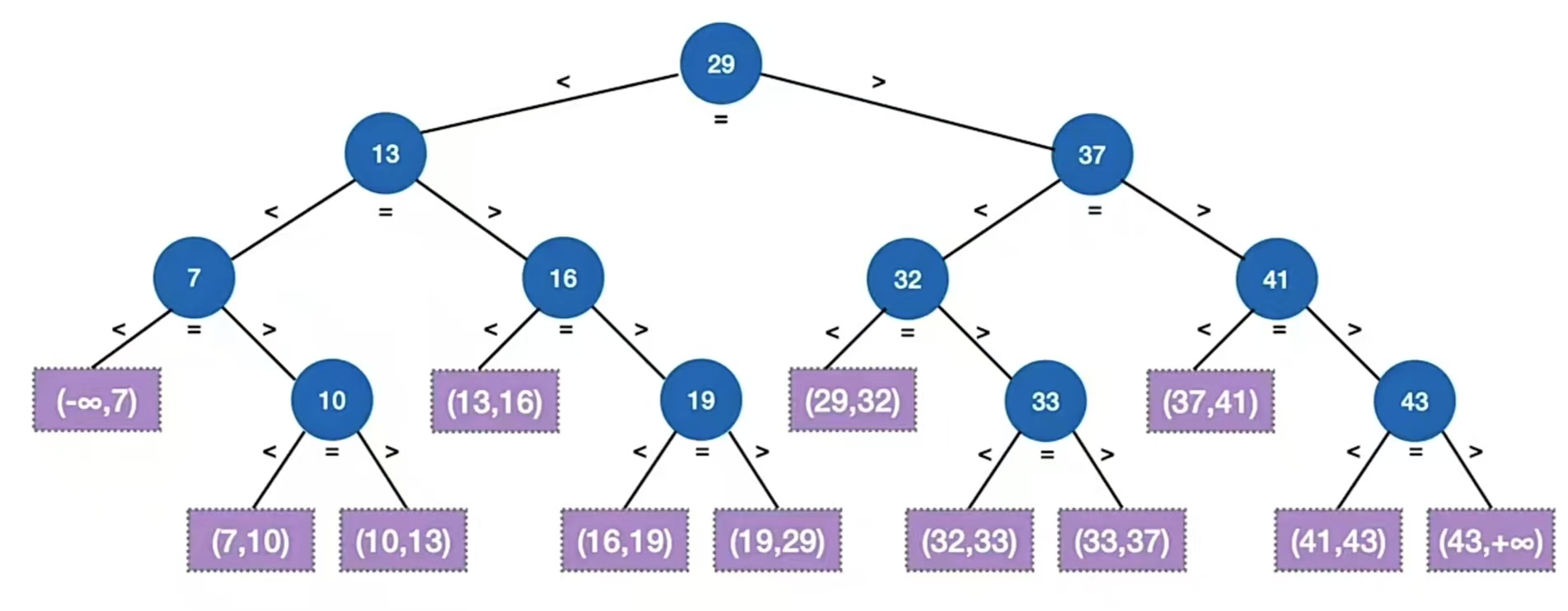
结构体也就关键字和左右指针：

//二叉排序树的结点
typedef struct BSTNode{int key;struct BSTNode *lchild,*rchild;
}BSTNode, *BSTree;

那我们再看这个树，其实是不是可以发现，它每一个结点都把无穷集（-∞，+∞）分割了一下，什么意思呢？就是比如根节点“29”，它就是把（-∞，+∞）分割成了（-∞，29），（29，+∞），（-∞，29）是根结点“29”左子树的区间，（29，+∞）是根结点“29”右子树的区间。

那如果不是“二叉”排序树，是多叉排序树呢？

二叉排序树有两个叉，几叉排序树就有几个叉。比如下面这个5叉排序树：

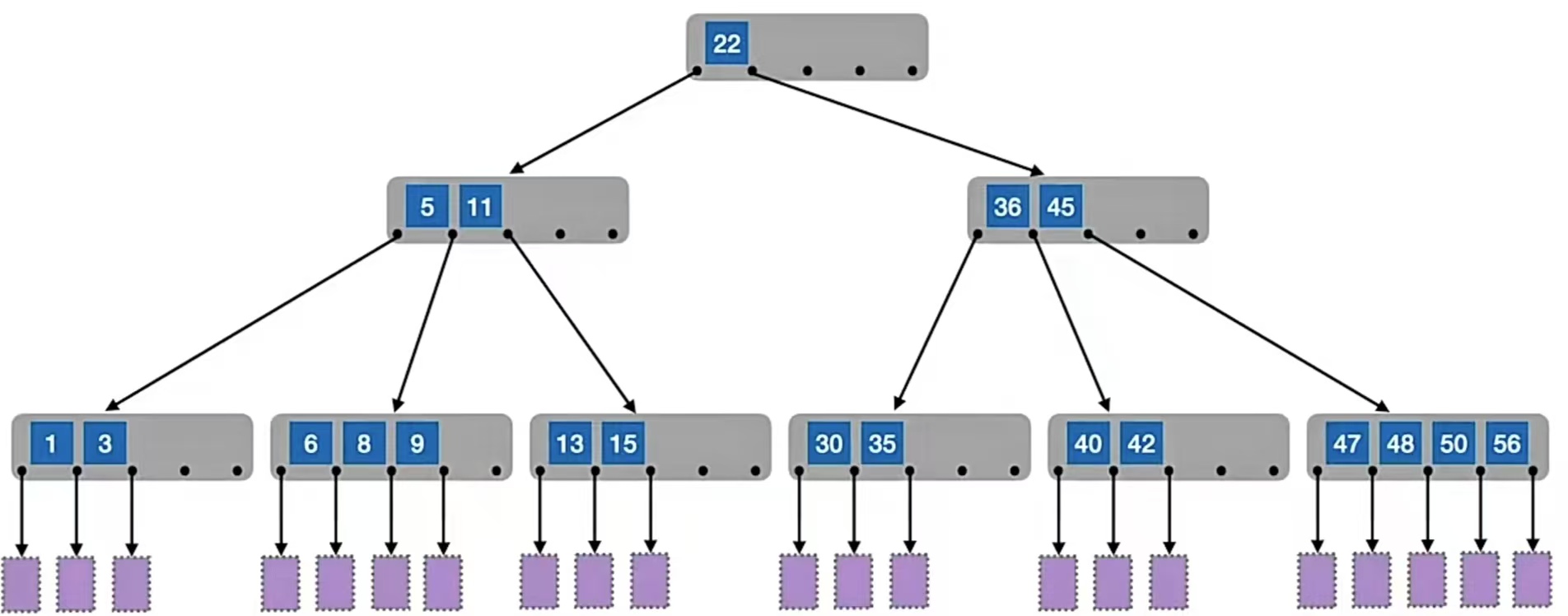
这个的本质也是分割区间。比如根结点“22”，把（-∞，+∞）分割成了（-∞，22），（22，+∞），（-∞，22）是根结点“22”左子树的区间，（22，+∞）是根结点“22”右子树的区间；再看右子树，右孩子结点里面有“36”，“45”，所以把（22，+∞）分割成了（22，36），（36，45），（45，+∞）……这样分割，查找到的就落在查找到的结点上，未查找到的就落在图中的最下层方形结点（失败结点）上。

比如结点“15”右边指针指向的那个失败结点，指向的区间就是（15, 22），比15大的比22小的没查找到就落在这个失败结点内这样。

//5叉排序树的结点
typedef struct BSTNode{int keys[4];			//最多4个关键字struct Node *child[5];  //最多5个孩子int num;			//结点中有几个关键字
};

为啥最多4个关键字？因为1个关键字两个叉（刚刚不是说了吗，分割为2个区间），所以4个关键字就是5个叉，而它是个5叉查找树，所以叉不能再多了，故最多4个关键字。

注：结点内关键字有序，所以我们在结点内查找的时候，既可以使用顺序查找，也可以使用折半查找。

比如我们在结点内用顺序查找，要查找“9”，则先和根节点“22”作对比，发现 9<22，所以去根节点的左子树找；在根节点的左孩子内进行顺序查找，发现 5<9<11，所以在“5”右边指向的那个结点内进行顺序查找，发现6<9,8<9,9=9,查找成功。同理，当落到右边指针指向为NULL时，查找失败。

当然，由上面那个5叉树的图可以看出，如果每个结点内关键字太少，导致树变高，要查更多层结点，效率就会很低。那么我们如何保证查找效率？其实就是不要让它那么“高”，不要让它每个结点内关键字太少。

so我们规定，m叉查找树中，除了根结点外，任何结点至少有 ⌈m/2⌉ 个分叉，即至少含有 ⌈m/2⌉ - 1 个关键字，这样就可以使得它并不会太“高”了。注意这里是“除了根结点”，因为如果我们整棵树只有1个元素，就没法满足这个“至少有 ⌈m/2⌉ 个分叉”，所以根结点可以只有1个元素2个分叉。

比如，对于5叉排序树，规定除了根结点外，任何结点都至少有3个分叉，2个关键字（⌈5/2⌉ = 3）。

但是我们规定了这个，还有一种可能就是全部都是左子树，这样就会很“高”，不如左右子树都有的情况“矮”，也就是说，不够“平衡”，树就会很高，要查很多层结点。

so我们又规定，m叉查找树中，对于任何一个结点，其所有子树的高度都要相同。

即，左右两边得一样高，不可以左边比右边高一层或者右边比左边高一层这样，也就是我们上面那个5叉查找树那种情况。

一、B树

1.B树

说了那么多，那么什么是B树呢？其实刚刚那个5叉查找树就是一棵满足B树要求的B树，再看一下：

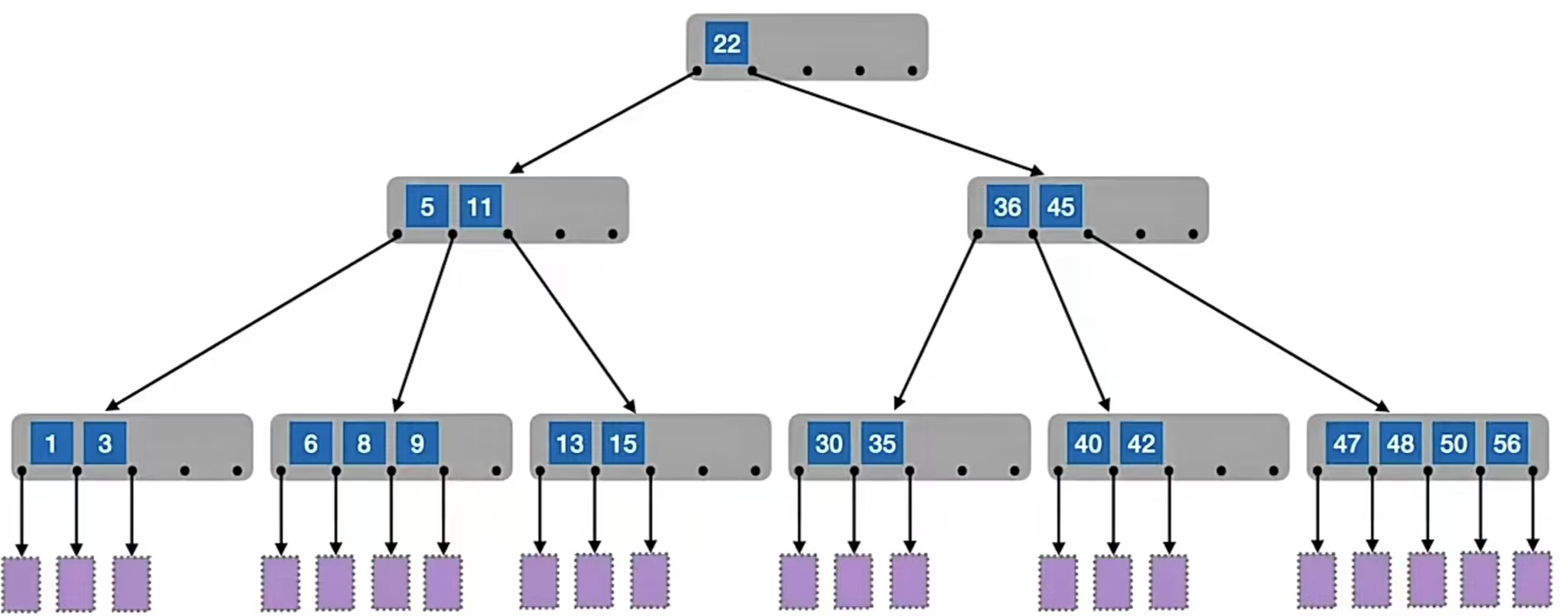
在B树中，我们把失败结点（最底下那个方形的）称为叶子结点，把最底下一层有关键字的称为终端结点。

准备好了吗？那么我们B树的定义要来喽~

B树，又称多路平衡查找树，B树中所被允许的孩子个数的最大值称为B树的阶，通常用 m 表示。一棵 m 阶B树或为空树，或为满足如下特性的m叉树：

1. 树中每个结点至多有 m 棵子树，即至多含有 m-1 个关键字；

2. 若根结点不是终端结点，则至少有两棵子树；

3. 除根结点外的所有非叶结点至少有 ⌈m/2⌉ 棵子树，即至少含有 ⌈m/2⌉ -1 个关键字；

4. 所有非叶结点的结构如下：

   n	P0	K1	P1	K2	P2	…	Kn	Pn

   其中，K_i（i=1,2，……，n）为结点的关键字，且满足 K₁＜K₂＜…＜K_n；P_i（i=0,1，……，n）为指向子树根结点的指针，且指针 P_i-1所指子树中所有结点的关键字均小于 K_i，P_i所指子树中所有结点的关键字均大于K_i，n（⌈m/2⌉-1 ≤ n ≤ m-1）为结点中关键字的个数；

5. 所有的叶结点都出现在同一层次上，并且不带信息（可以视为外部结点或类似于折半查找判定树的查找失败结点，实际上这些结点不存在，指向这些结点的指针为空）。

什么意思呢？别介，一条一条看。

先看第1条，m阶B树显然最多有m个叉，所以每个结点至多有 m 棵子树，那么就最多有 m-1 个关键字；

第2条，根节点不是终端结点是指这个B树不止有一层（只有一层的话那么根结点不就是终端结点嘛），所以这个就是规定根结点是至少有1个关键字的，不然不就是个空的了，所以至少有2棵子树；

第3条，也就是我们刚刚为了保证查找效率让它不要那么“高”做的规定，除根结点的所有非叶结点（有关键字的结点，也就是不是失败结点的结点）至少有 ⌈m/2⌉ 棵子树，即至少含有 ⌈m/2⌉ -1 个关键字，这样就可以使得它并不会太“高”了；

第4条，其实就是满足二叉排序树的定义，要满足左≤根≤右，结点内也是有序的，因为B树也是一棵水灵灵的二叉排序树；

第5条，所谓的叶结点就是失败结点，因为我要保持B树的平衡，所以左右子树都是一样高的，所以失败结点一定是会出现在同一层的，不然的话就不满足我们规定的“平衡”了。

看起来很多，但其实我们归纳总结一下也就是下面三个特性：

m 阶B树的核心特性：

1. 根结点的子树数 ∈ [2,m]，关键字数 ∈ [1,m-1]；
   其他结点的子树数 ∈ [ ⌈m/2⌉ ，m]；关键字数 ∈ [ ⌈m/2⌉-1 ，m-1 ]
2. 对任一结点，其所有子树高度都相同
3. 关键字的值：子树0<关键字1<子树1<关键字2<子树2……（类比二叉查找树，左<中<右）

这就是总结了一下，其实就是根结点和其他结点的关键字数有最小和最大限制、平衡、满足二叉排序树特性，就这些。

2.B树的高度

那么我们B树的高度是多高呢？即，含 n 个关键字的 m 阶B树，最小高度、最大高度是多少？

最小高度——让每个结点尽可能地满

假设我们B树的高度为h

每个结点有 m-1 个关键字，m个分叉，则装满的情况下，关键字总数为(m-1)*结点个数，结点个数第一层1个，第二层m个（m个分叉），第三层m²个（第二层每个有m个分叉，第二层共m个）……以此类推，h层一共有(1+m+m²+……+m^h-1)个结点，所以h层装满的情况下关键字个数为(m-1)(1+m+m²+……+m^h-1)，那么我们的关键字肯定是小于等于这个树的，所以

n ≤ (m-1)(1+m+m²+……+m^h-1)

所以 h ≥ log_m（n+1），含 n 个关键字的 m 阶B树，最小高度为 log_m（n+1）

最大高度——让每个结点包含的关键字、分叉尽可能的少。

各层结点至少有：第一层 1、第二层 2、第三层 2⌈m/2⌉……第h层 2⌈m/2⌉^h-2 （因为根结点至少一个，除了根节点的其他结点至少有⌈m/2⌉个），第h+1层共有叶子结点（失败结点） 2⌈m/2⌉^h-1个

又因为 n个关键字的B树必有n+1个叶子结点（我说一下哈，这可以通过两种方式得到这个结论，一个是我们刚刚说到的“分区间”，每个关键字都把（-∞，+∞）分割开，所以我们分割后就有 n+1 个区间，失败结点（叶子结点）就分别代表这些区间，所以n个关键字的B树必有n+1个叶子结点）。

我们第h+1层最少有的叶子结点数为2⌈m/2⌉^h-1个， 所以我们的B树的叶子节点数一定大于这个树，即 n+1 ≥ 2⌈m/2⌉^h-1

所以 h ≤ log_⌈m/2⌉（n+1)/2 +1，含 n 个关键字的 m 阶B树，最大高度为 log_⌈m/2⌉（n+1)/2 +1

更直观的话，我们记 k=⌈m/2⌉，则：

	最少结点数	最少关键字数
第一层	1	1
第二层	2	2(k-1)
第三层	2k	2k(k-1)
第四层	2k2	2k2(k-1)
…	…	…
第 h 层	2kh-2	2kh-2(k-1)

h层的m阶B树至少包含关键字总数 1+2(k-1)(k⁰+k¹+k²+…+k^h-2) = 1+ 2(k^h-1-1)

若关键字总数少于这个值，则高度一定小于h（这写的啥啊，其实就是如果高度为h，一定大于这个值），因此 n ≥ 1+ 2(k^h-1-1)，得，h ≤ log_k（n+1)/2 +1 = log_⌈m/2⌉（n+1)/2 +1

即，含 n 个关键字的 m 阶B树，log_m（n+1）≤ n ≤ log_⌈m/2⌉（n+1)/2 +1

二、B树的插入删除

1.插入

现在我们来一个一个插入5阶B树（结点关键字个数 ⌈m/2⌉-1 ≤ n ≤ m-1，即：2≤n≤4，此处省略失失败结点），用一个栗子来看看B树是怎么插入的：

首先，我们插入“25”，那么它一定是先插入到根结点上，即：

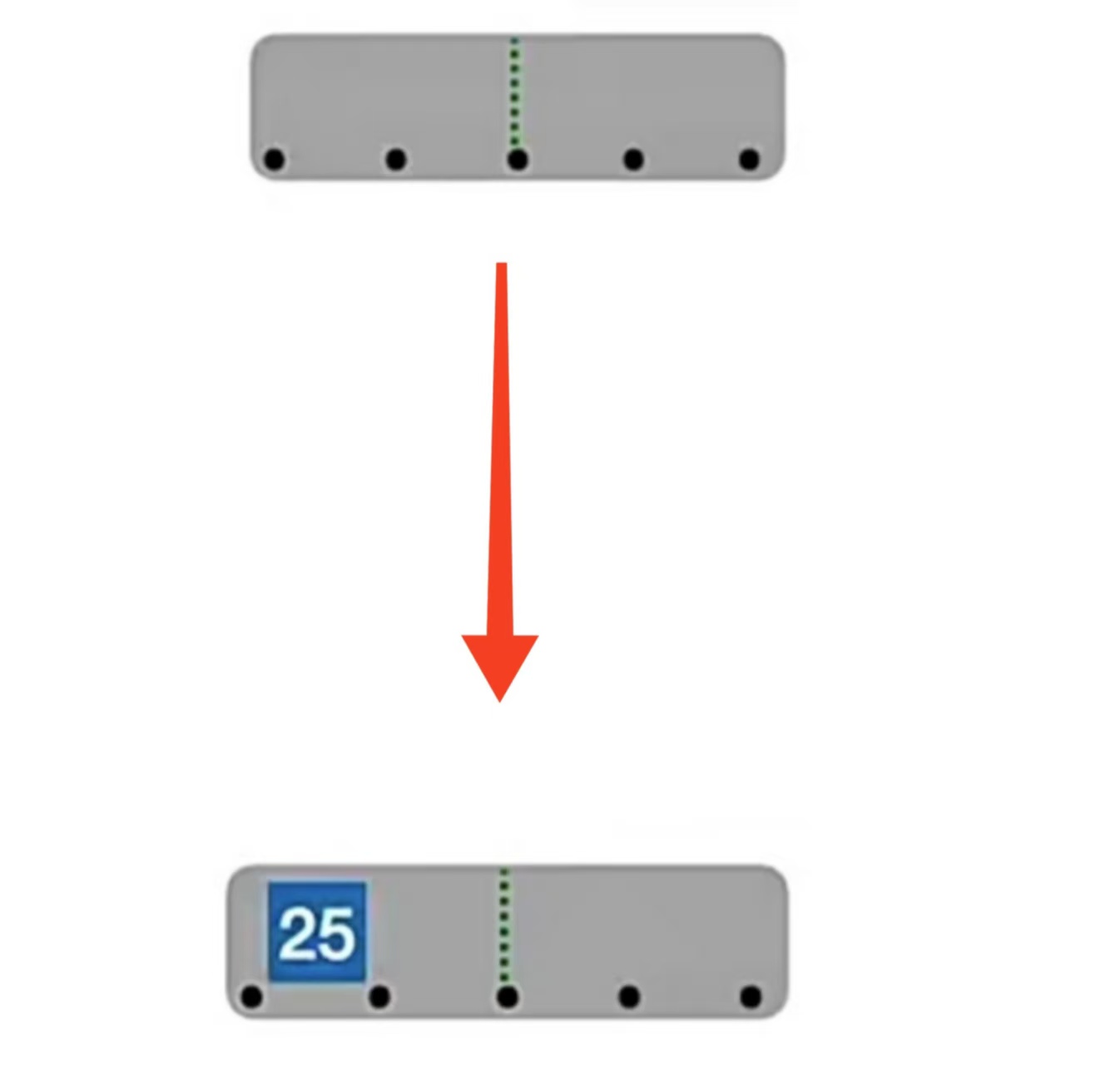
那么我们再插入“38”：

插入“49”：

插入“60”：

接下来，我们插入“80”，我们会发现根结点已经满了，放不下了，所以我们要“分裂”：

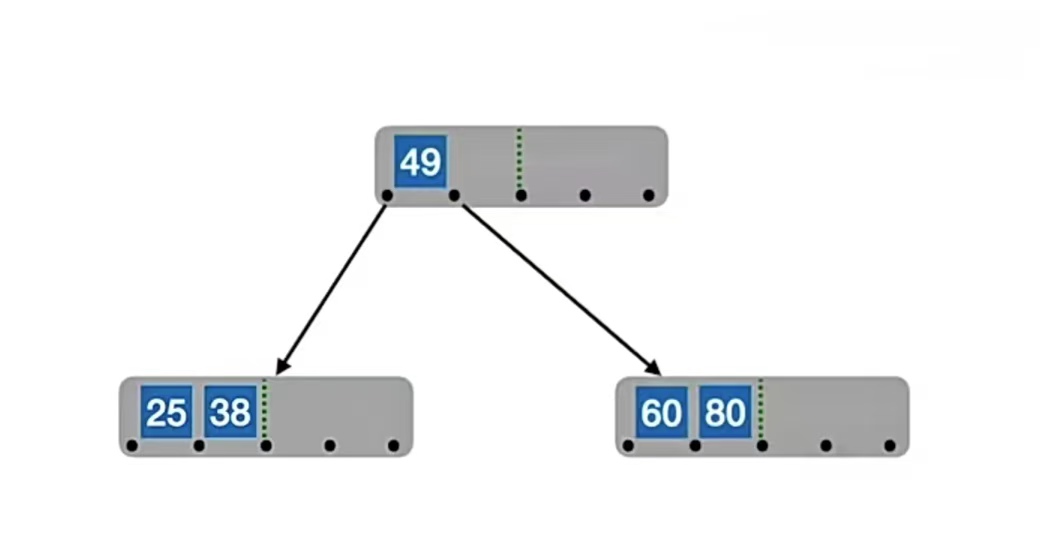
在插入key后，若导致原结点关键字数超过上限，则从中间位置（⌈m/2⌉）将其中的关键字分为两部分，左部分包含的关键字放在原结点中，右部分包含的关键字放到新结点中，中间位置（⌈m/2⌉）的结点插入原结点的父结点。

那我们发现，插入“80”之后，“80”放“60”右边已经“冒了”，所以我们应该“分裂”，我们的中间位置⌈m/2⌉=⌈5/2⌉=3，也就是“49”，所以“49”左边的“25”，“38”放在原结点中，右边的“60”，“80”放在新结点中，“49”变成原结点的父结点，也就是上图那个样子。

那我们就会发现，其实根结点有位置，底下左右孩子两个结点也有位置，那我们下面如果要插入新元素，插入到哪里呢？我们有一个插入规则：

新元素一定是插入到最底层“终端结点”，用“查找”来确定插入位置。

就是插入到最底层。比如现在我们要插入“90”，我们先查找它应该插入到什么位置，90>49，所以应该往右子树找；90>60，90>80，此时应该往下找，发现已经是终端结点，所以插入到“80”右边，如下：

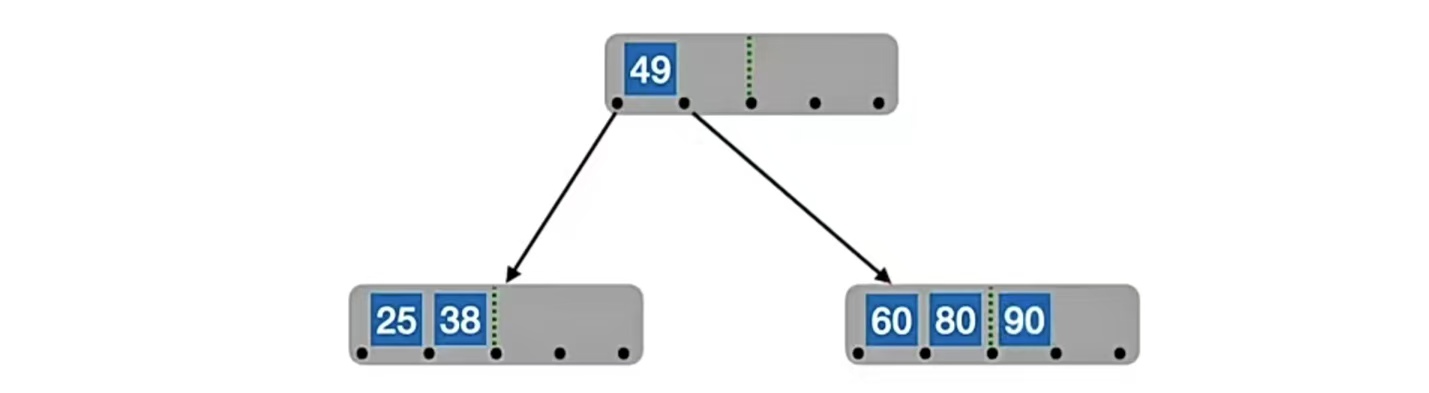
为啥一定要插入到最底层？因为我们B树的定义就是，B树的失败结点只能出现在最下面一层，如果“90”插入到“49”旁边了，那么“90”右边指针指向的就是失败结点null，和“49”左右子树的失败结点就不是同一层了，就像下面这样：

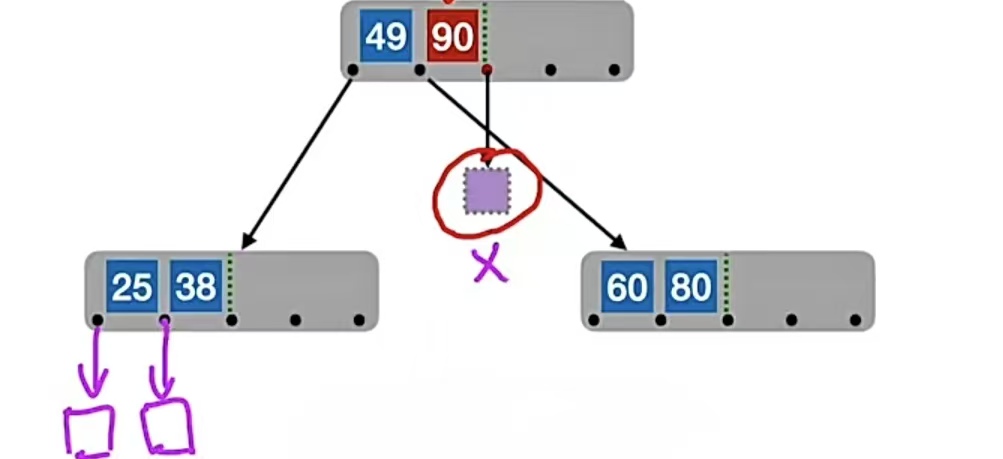
后面我们再插入“99”，还是插入到终端结点：

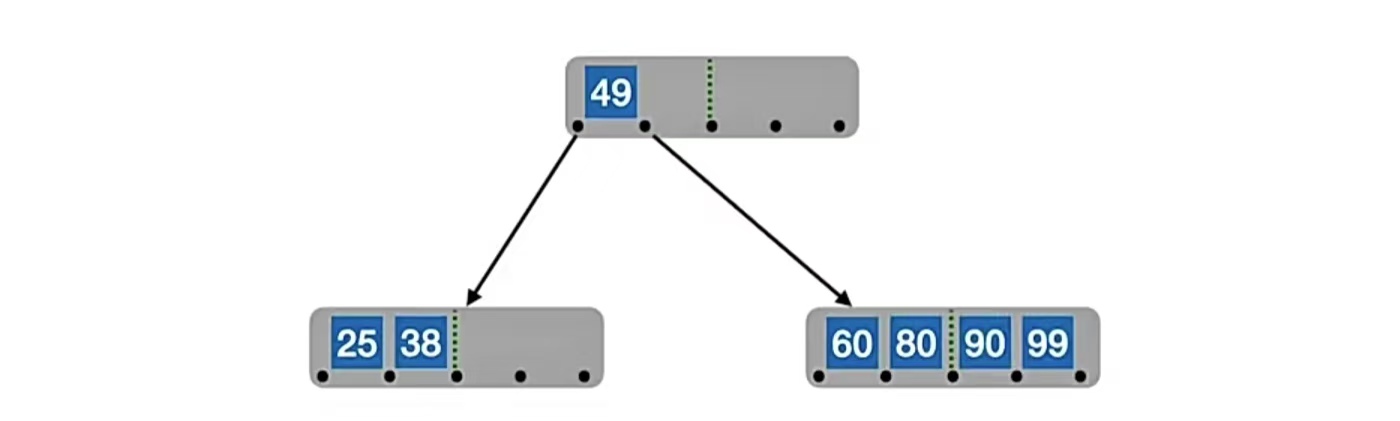
我们再插入“88”，查找它应该插入的位置，发现它应该插入到“49”右孩子结点中的“80”和“90”中间，即：

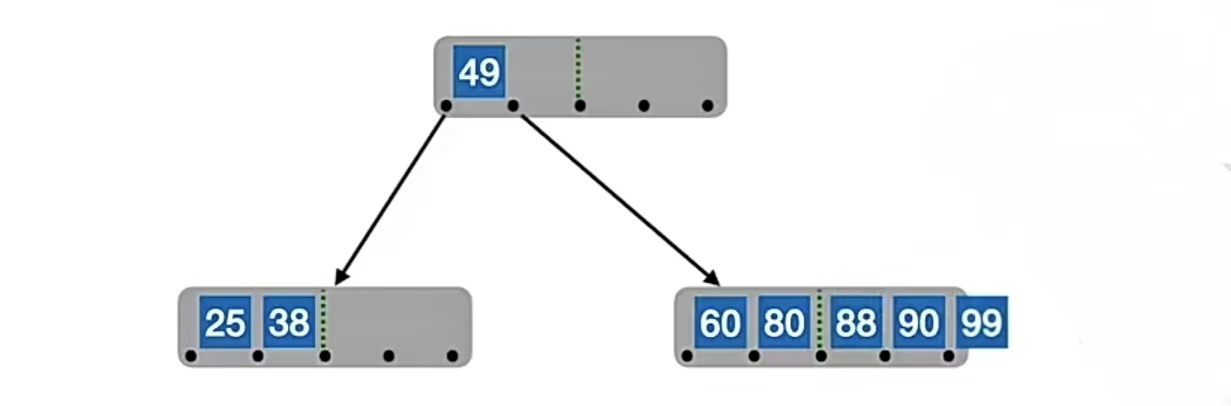
所以我们又要分裂了。我们的中间位置⌈m/2⌉=⌈5/2⌉=3，也就是“88”，所以“88”左边的“60”，“80”放在原结点中，右边的“90”，“99”放在新结点中，“88”变成原结点的父结点，但是原结点已经有父结点了，所以就放到“49”的右边，也就是这样：

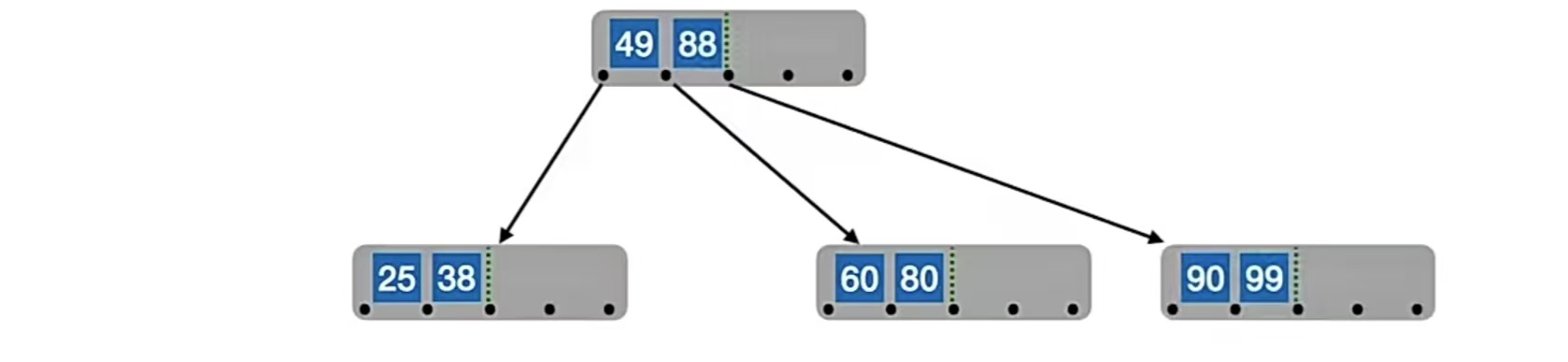
我们再插入结点“83”，49<83<88，找到它的查找位置是,49、88之间的指针指向的结点内，开始对比这个结点的数据。60<83，80<83，这个结点又是终端结点，所以插入到“80”的右边：

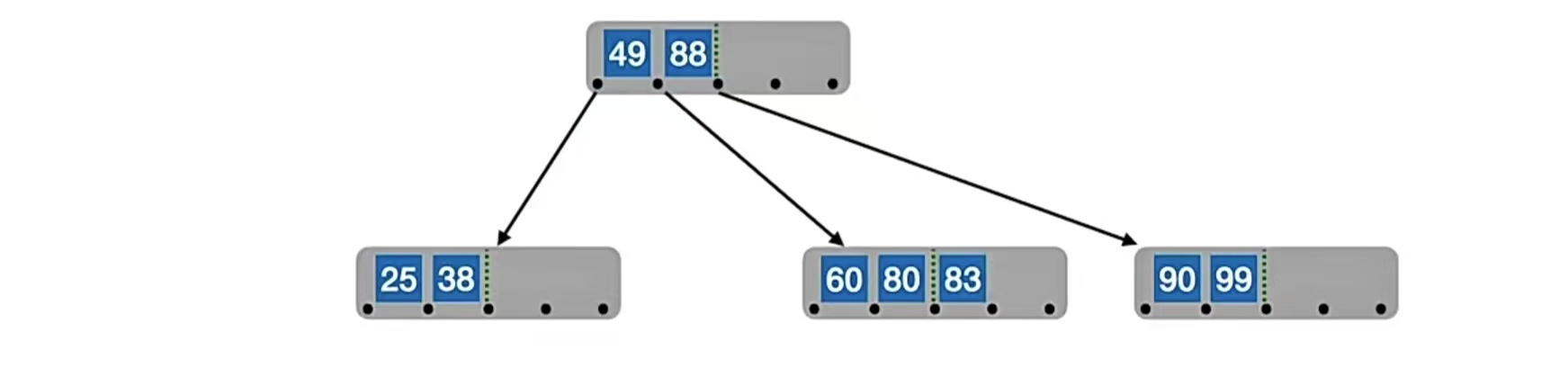
再插入“87”，同样的，找到它的插入位置，在“83”右边：

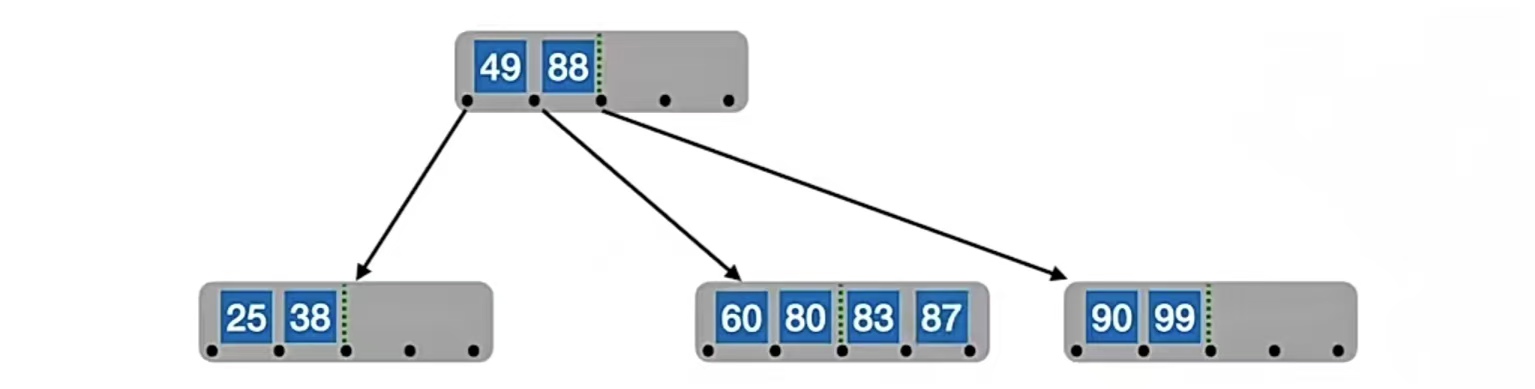
再插入结点“70”，还是按照原来的办法插入，发现又“冒了”：

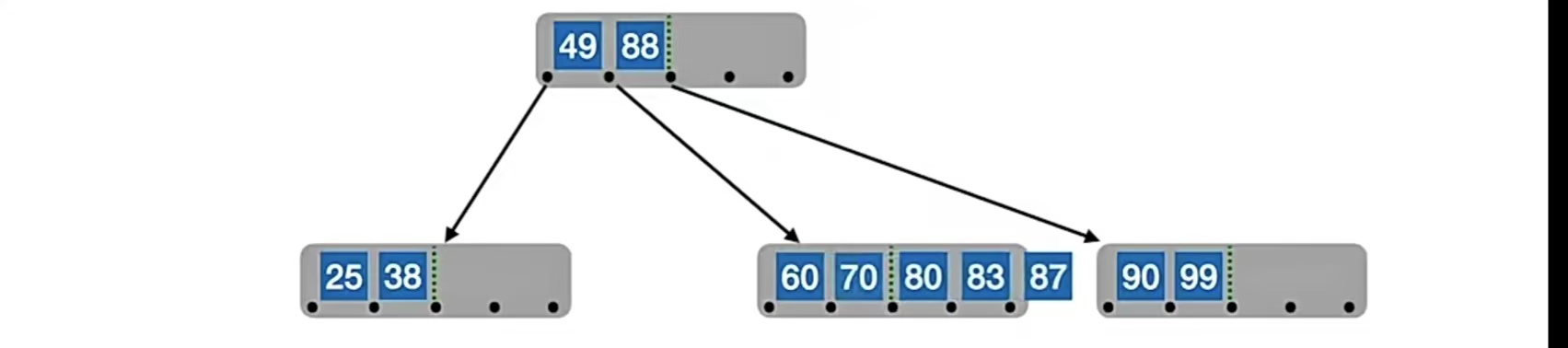
所以我们又双要分裂了。我们的中间位置⌈m/2⌉=⌈5/2⌉=3，也就是“80”，所以“80”左边的“60”，“70”放在原结点中，右边的“83”，“87”放在新结点中，“80”变成原结点的父结点，但是原结点已经有父结点了，所以就放到“49”的右边，“88”的左边，也就是这样：

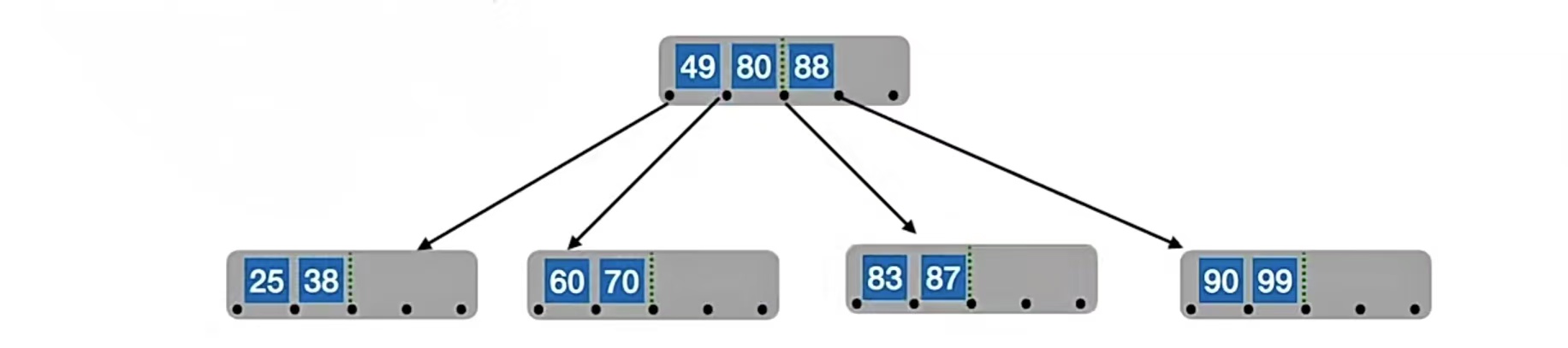
我们再插入“92”，“93”，“94”，就是这样又冒了的情况：

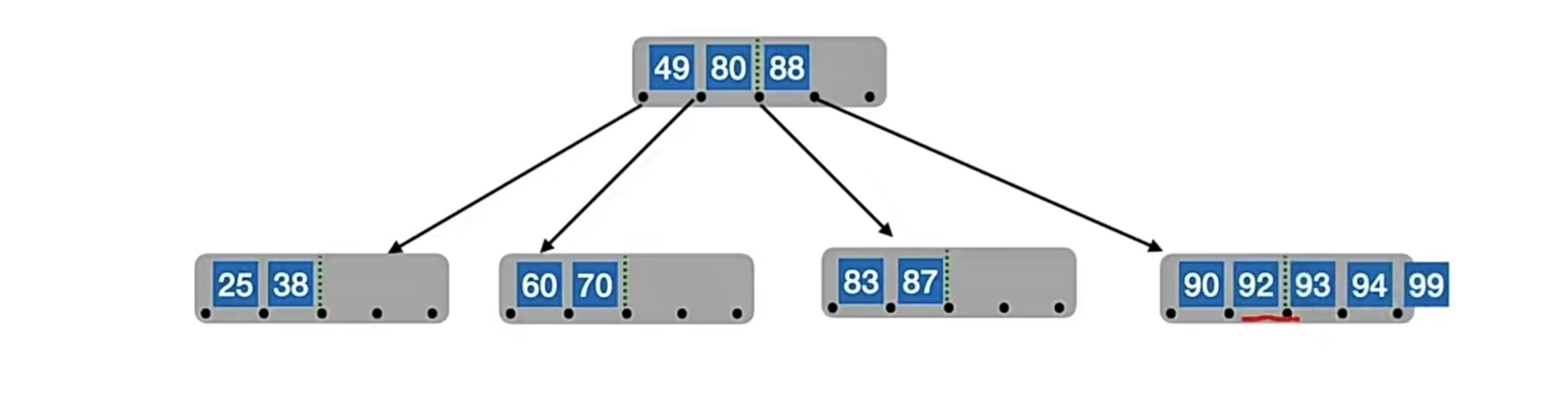
所以我们又双叒要分裂了。我们的中间位置⌈m/2⌉=⌈5/2⌉=3，也就是“93”，所以“93”左边的“90”，“92”放在原结点中，右边的“94”，“99”放在新结点中，“93”变成原结点的父结点，但是原结点已经有父结点了，所以就放到“88”的右边，也就是这样：

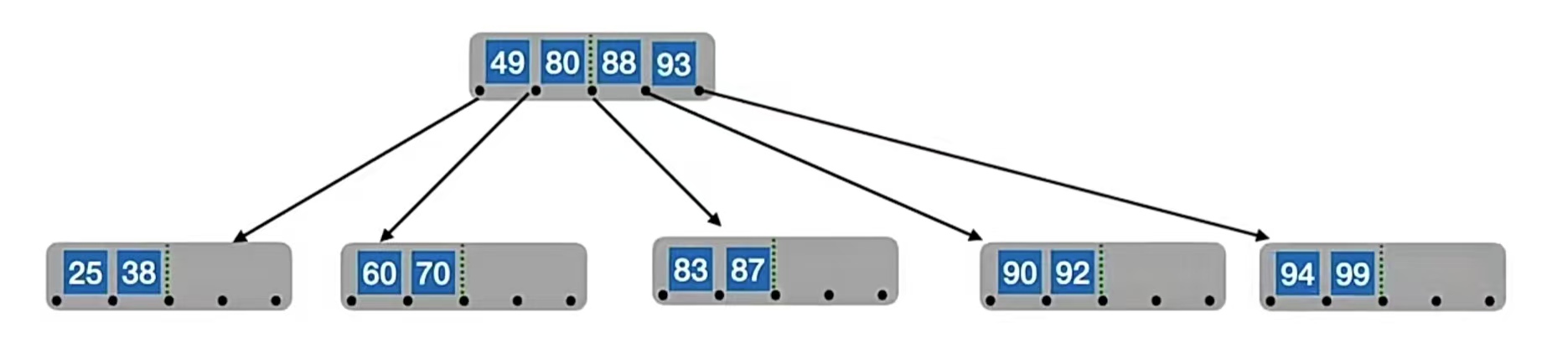
我们再插入“73”，“74”，“75”，就是这样又冒了的情况：

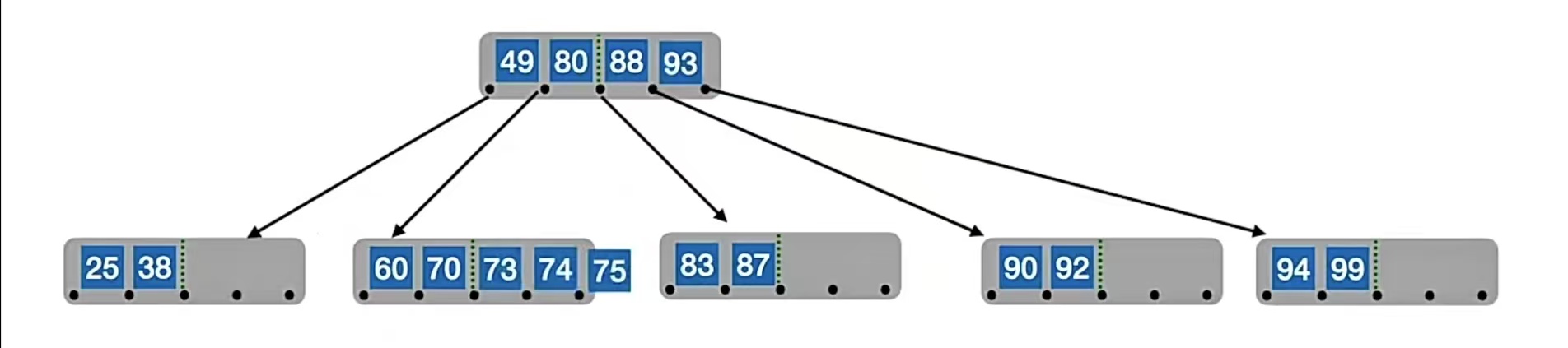
所以我们又双叒叕要分裂了。我们的中间位置⌈m/2⌉=⌈5/2⌉=3，也就是“73”，所以“73”左边的“60”，“70”放在原结点中，右边的“74”，“75”放在新结点中，“73”变成原结点的父结点，但是原结点已经有父结点了，所以就放到“49”的右边，“80”的左边，也就是这样：

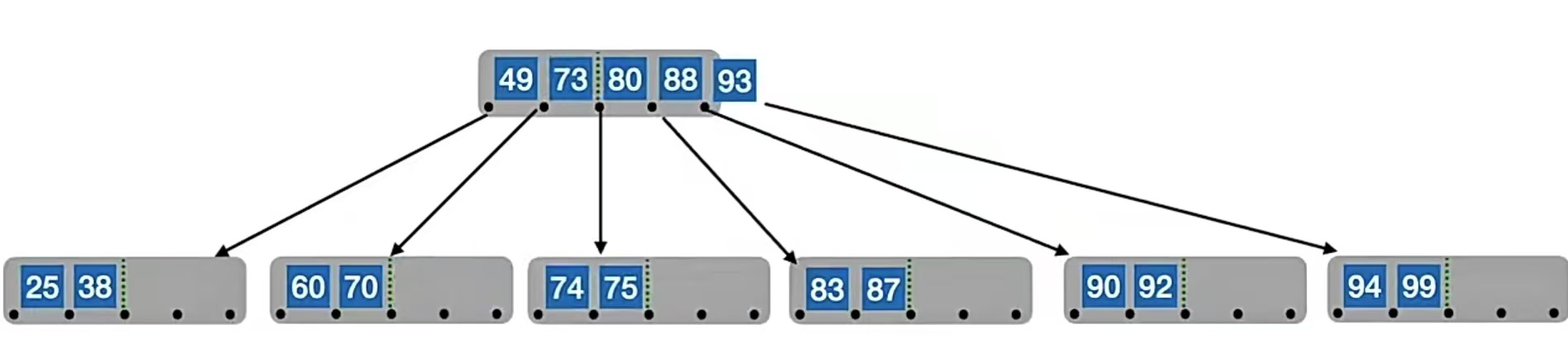
但是！！！！此时我们会发现根结点也冒了，所以我们又双叒叕又要分裂，这次分裂的是根结点。我们的中间位置⌈m/2⌉=⌈5/2⌉=3，也就是“80”，所以“80”左边的“49”，“73”放在原结点中，右边的“88”，“93”放在新结点中，“80”变成原结点的父结点，也就是这样：

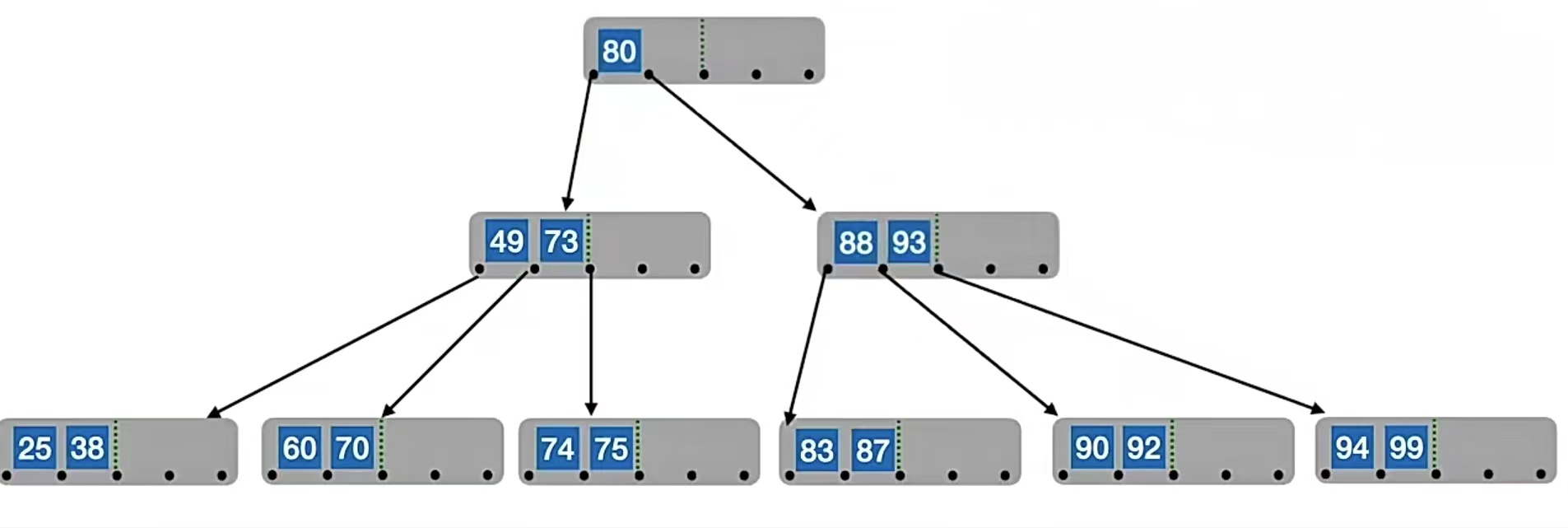
好了，经过上面的栗子，我们现在都会B树的插入了。其实就是先找，找要插到哪（注意得是终端结点），完了再看看是不是“冒了”，“冒了”就分裂，把中间位置⌈m/2⌉的元素挤到上面去。

要注意我们的核心要求：

1. 对m阶B树——除根节点外，结点关键字个数 ⌈m/2⌉ - 1 ≤ m-1
2. 子树0 ＜ 关键字1 ＜ 子树1＜ 关键字2 ＜ 子树2 ＜ ……

还有就是，新元素一定是插入到最底层“终端节点”，用“查找”来确定插入位置

在插入key后，若导致原结点关键字数超过上限，则从中间位置（ ⌈m/2⌉ ）将其中的关键字分为两部分，左部分包含的关键字放在原结点中，右部分包含的关键字放到新结点中，中间位置（ ⌈m/2⌉ ）的结点插入原结点的父结点。

若此时导致 父结点的关键字个数也超过了上限，则继续进行这种分裂操作，直至这个过程传到根结点为止，进而导致B树高度增加1。

2.删除

讲完了B树的插入，现在我们来讲B树的删除。

这是一棵水灵灵的B树：

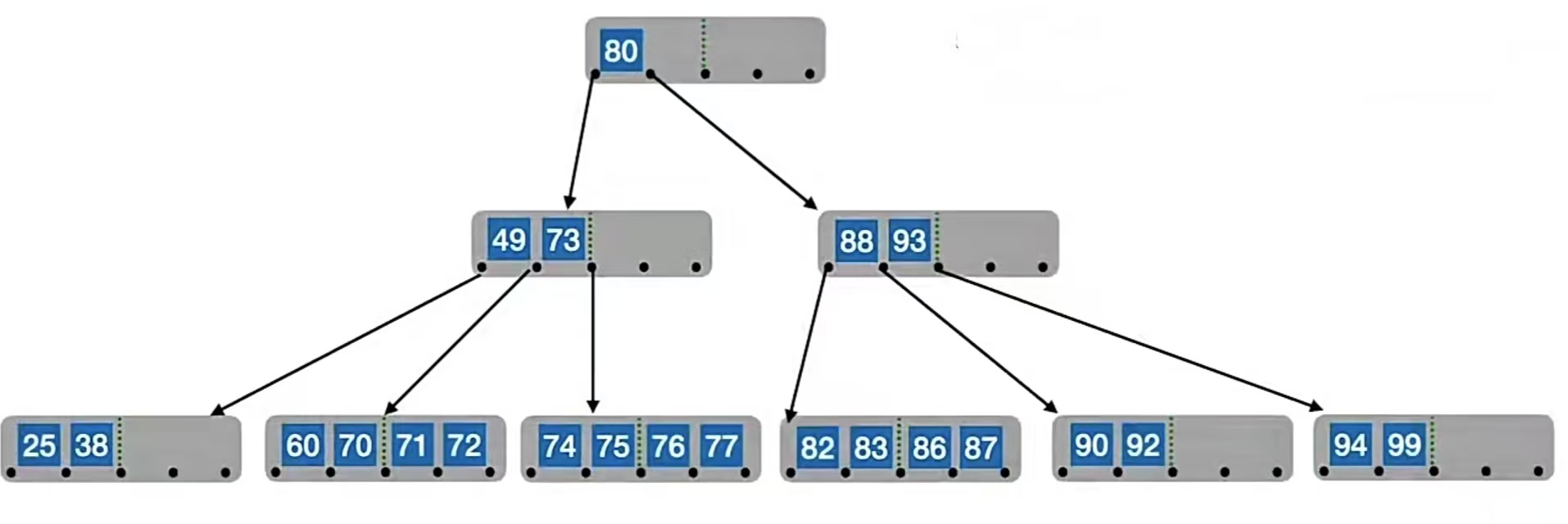
比如我们要删除“60”

若被删除关键字在终端结点，则直接删除该关键字（要注意结点关键字个数是否低于下限 ⌈m/2⌉-1）

由于“60”在终端结点，且删除后关键字个数为3个，下限 ⌈m/2⌉-1=2，并没有低于B树的结点关键字下限，所以直接删就好了：

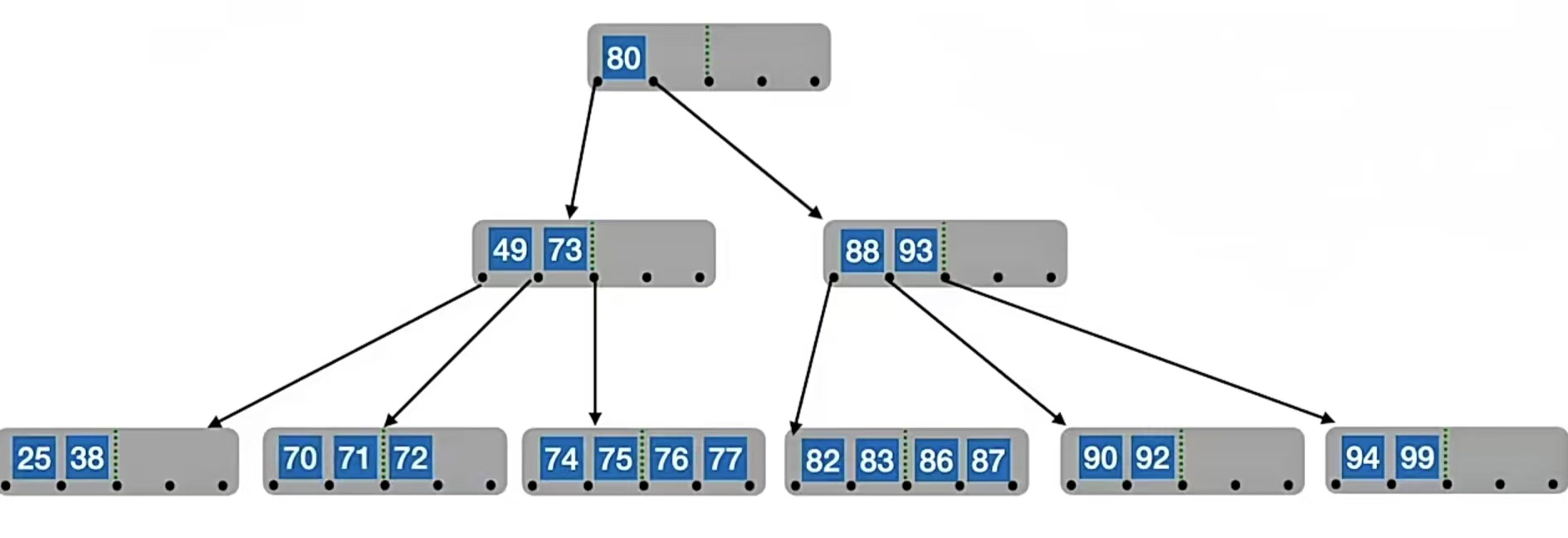
那如果我们删除的不是终端结点该怎么办，比如如果我们要删除“80”呢？其实和二叉排序树的删除一样的，都是让直接前驱/直接后继代替，然后再删，这样可以完美维持我们二叉树的左<根<右的性质：

若被删除关键字在非终端结点，则用直接前驱或直接后继来替代被删除的关键字
直接前驱：当前关键字左侧指针所指子树中“最右下”的元素
直接后继：当前关键字右侧指针所指子树中“最左下”的元素

那我们如果用直接前驱来代替，要删除“80”，先得找“80”的直接前驱。我们找“80”左侧指针所指子树中“最右下”的元素，也就是“77”，所以我们用“77”来替代“80”，再转化为删除“77”的操作。由于“77”在终端结点，所以可以直接删，于是我们的B树就变成了这样：

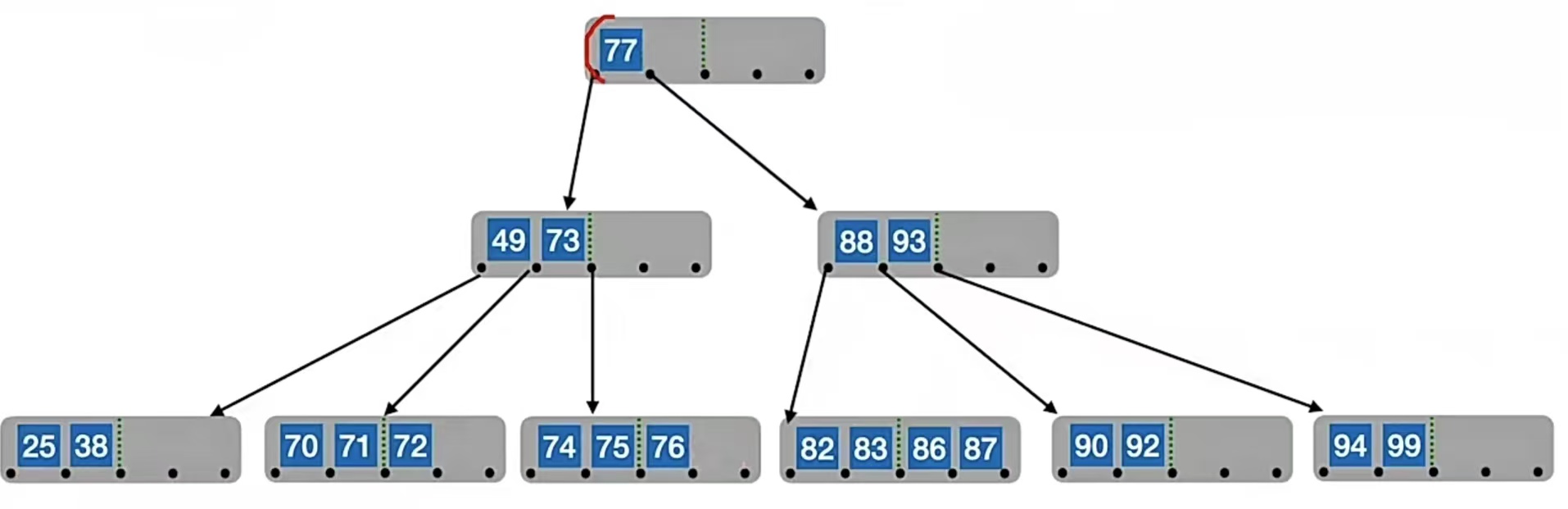
那如果我们要删除“77”呢？它也是非终端结点，这次我们用直接后继来代替。我们找“77”右侧指针所指子树中“最左下”的元素，也就是“82”，所以我们用“82”来替代“77”，再转化为删除“82”的操作。由于“82”在终端结点，所以可以直接删，于是我们的B树就变成了这样：

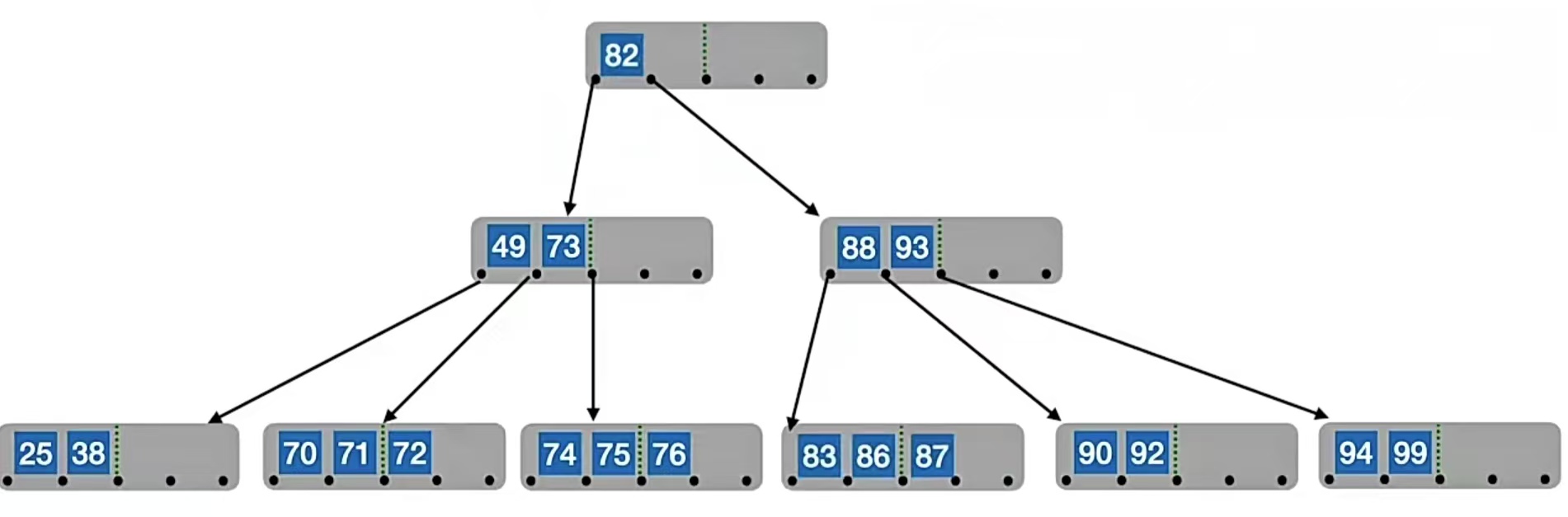
其实我们可以发现，对非终端结点关键字的删除，必然可以转化为对终端结点的删除操作，因为先用直接前驱/直接后继代替嘛，既然是直接前驱/直接后继，那肯定在终端结点上。

但是你以为我们B树的删除就这样讲完结束了吗？no no no，别忘了我们之前说的，要注意结点关键字个数是否低于下限 ⌈m/2⌉-1，所以肯定会有删完了之后结点关键字个数低于下限 ⌈m/2⌉-1的情况。

比如我们要删除“38”，直接删不做任何操作就会变成下面这样：

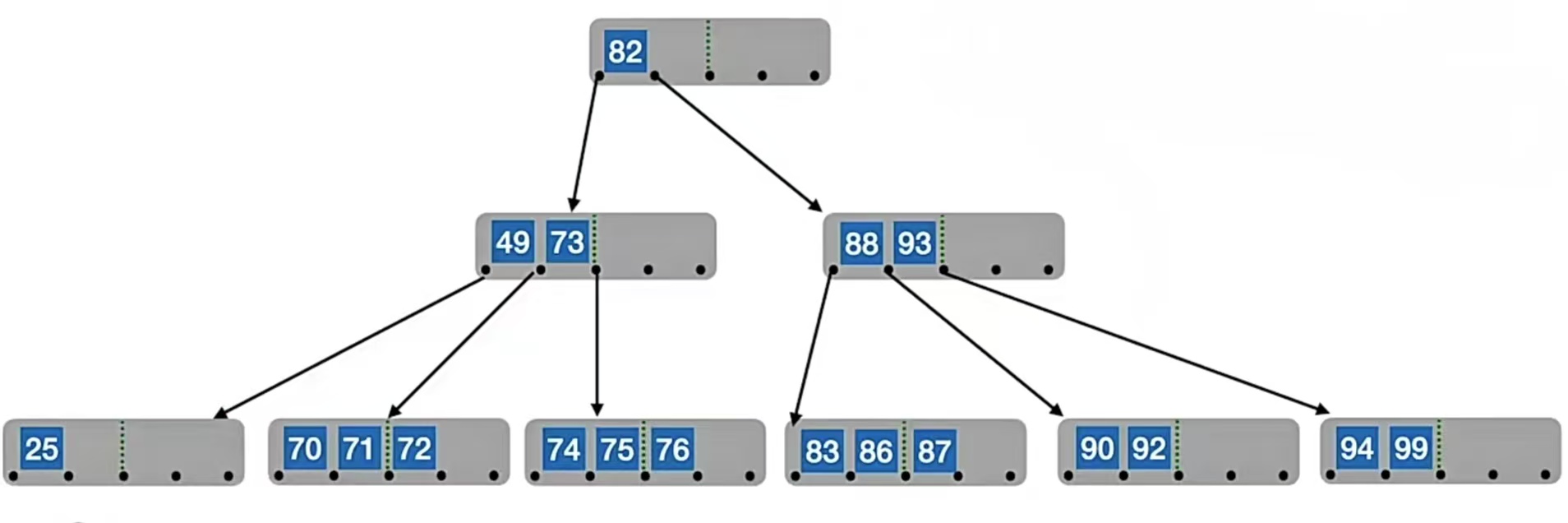
此时就会发现最左下那个结点中的关键字只有1个，个数低于下限 ⌈m/2⌉-1=2了。

我们个数不够最低下限，怎么办？遇到事情不要慌，先发个朋友圈（bushi，不够的话没关系，问别人借一个就够了：

兄弟够借。若被删除关键字所在结点删除前的关键字个数低于下限，且与此结点右（或左）兄弟结点的关键字个数还很宽裕，则需要调整该结点、右（或左）兄弟结点及其双亲结点（父子换位法）

比如我们刚刚删除“38”后，最左下的那个结点不够了，我们看到它的右兄弟还很宽裕（右结点有3个元素，就算被借走一个，那它还有2个元素，仍然满足个数不低于下限 ⌈m/2⌉-1=2），就敲开了他的门……于是把“70”给借走，则右结点就剩“71”和“72”了，我们原本的那个结点就变成了“25”和“70”：

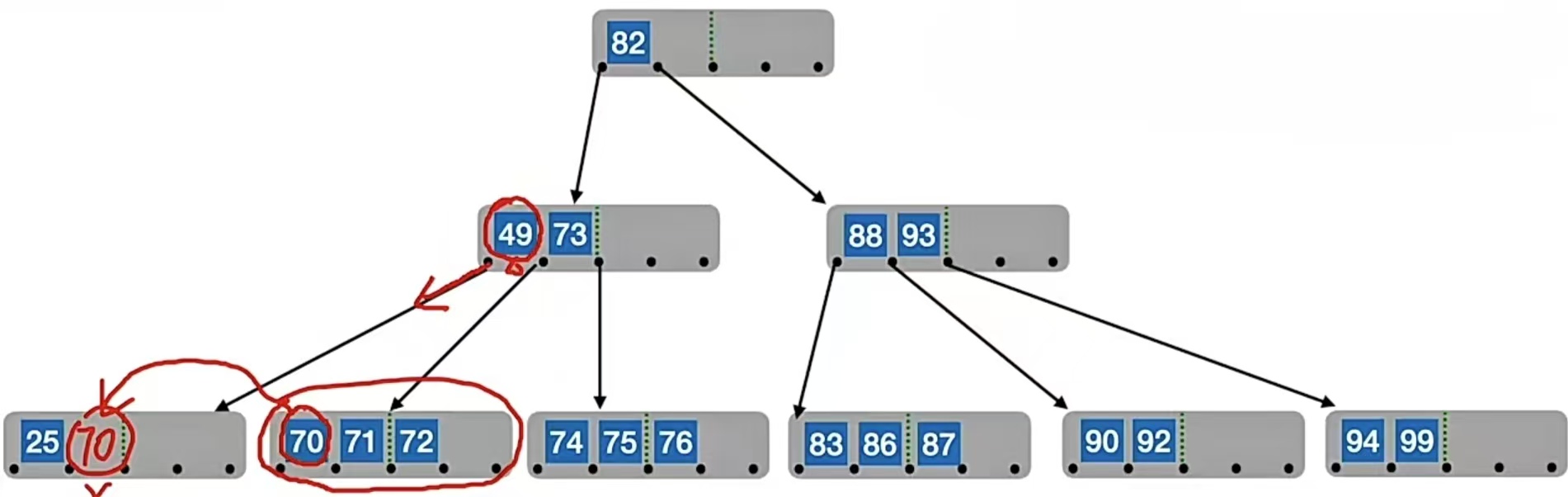
但是！！！这样是不是违反了我们二叉排序树的特性，因为它们的父结点中49<70，所以就破坏了二叉排序树，所以我们要把“49”和“70”调换，即：

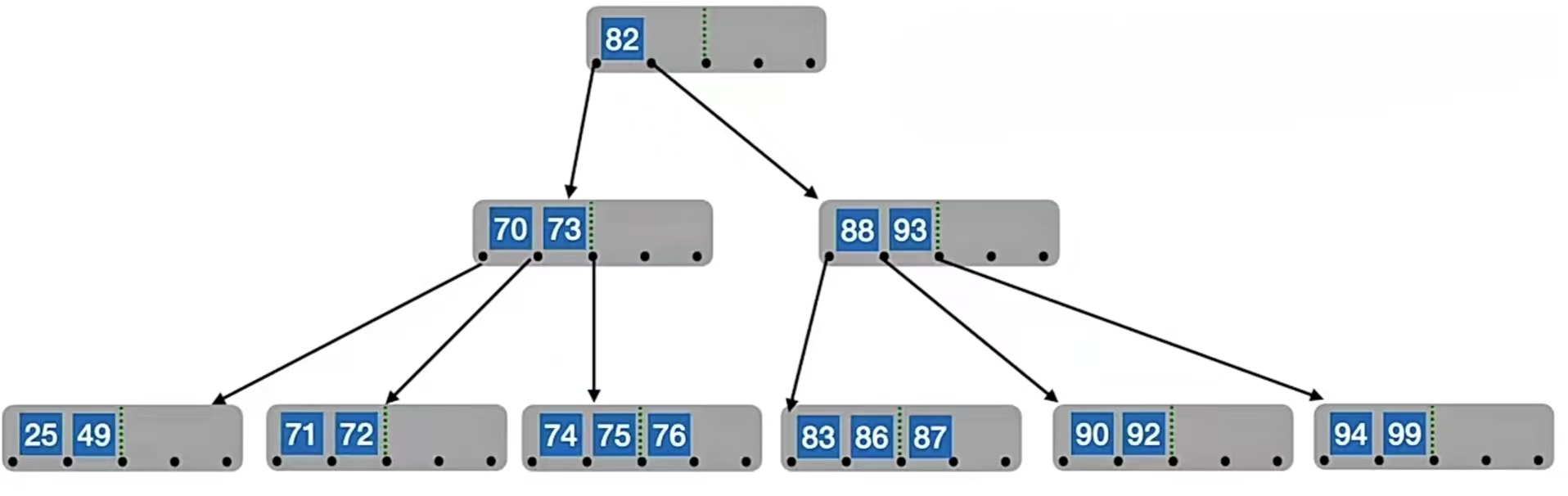
你有没有发现，其实借来的变成了“49”，也就是我们删除后不够的那个结点的直接后继……

说白了，就是当右兄弟很宽裕时，用当前结点的后继、后继的后继来填补空缺；
当左兄弟很宽裕时，用当前结点的前驱、前驱的前驱来填补空缺即可。

啥意思呢？举个栗子就明白了。

比如我们删除“90”，删除后如下：

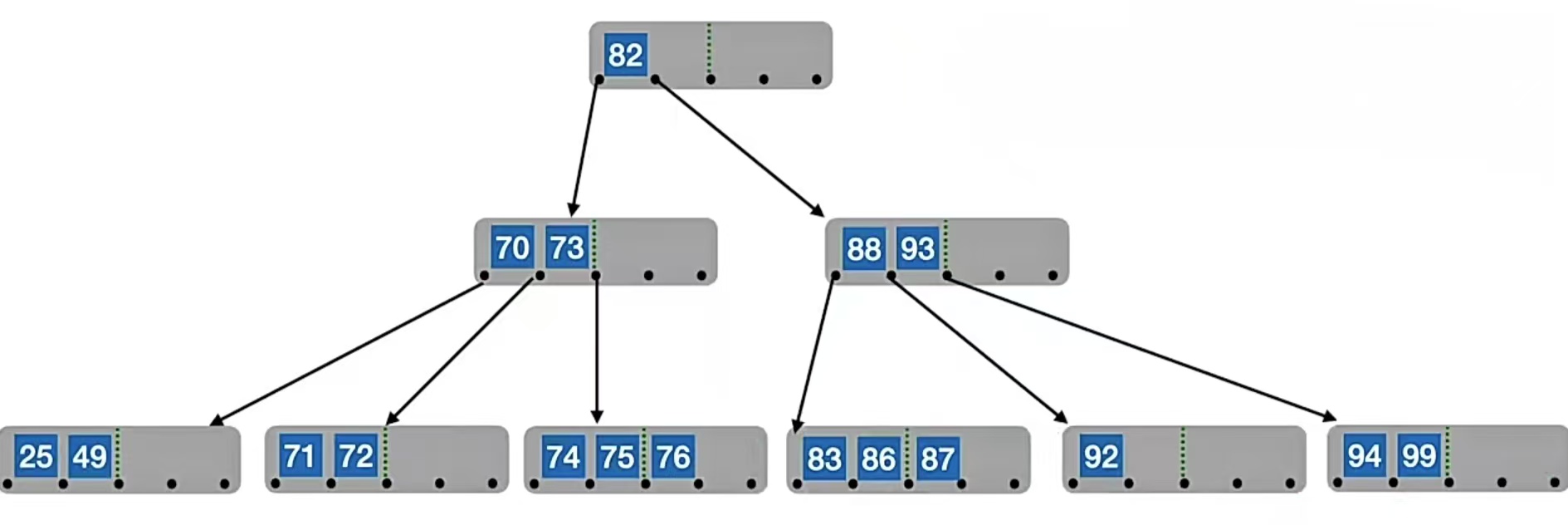
我们发现被删除元素的那个结点中的关键字只有1个，个数低于下限 ⌈m/2⌉-1=2了，右兄弟不够借，左兄弟够借（左兄弟有3个元素，就算被借走一个，那它还有2个元素，仍然满足个数不低于下限 ⌈m/2⌉-1=2），所以我们用前驱、前驱的前驱来填补空缺，前驱为“88”，前驱的前驱为“87”，所以把“88”放到被删除的那个结点里面，“87”放到前驱结点里面，即：

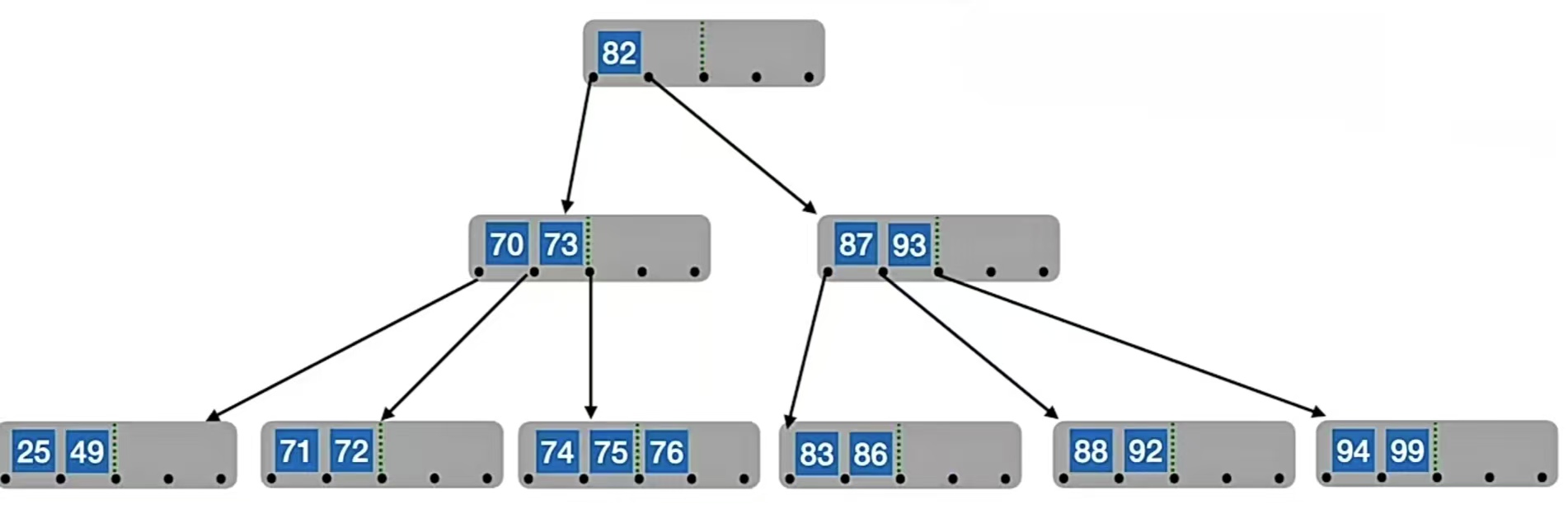
本质：要永远保证 子树0<关键字1<子树1<关键字2<子树2……

再来个“不够借”的例子，比如我们要删除“49”，删除之后：

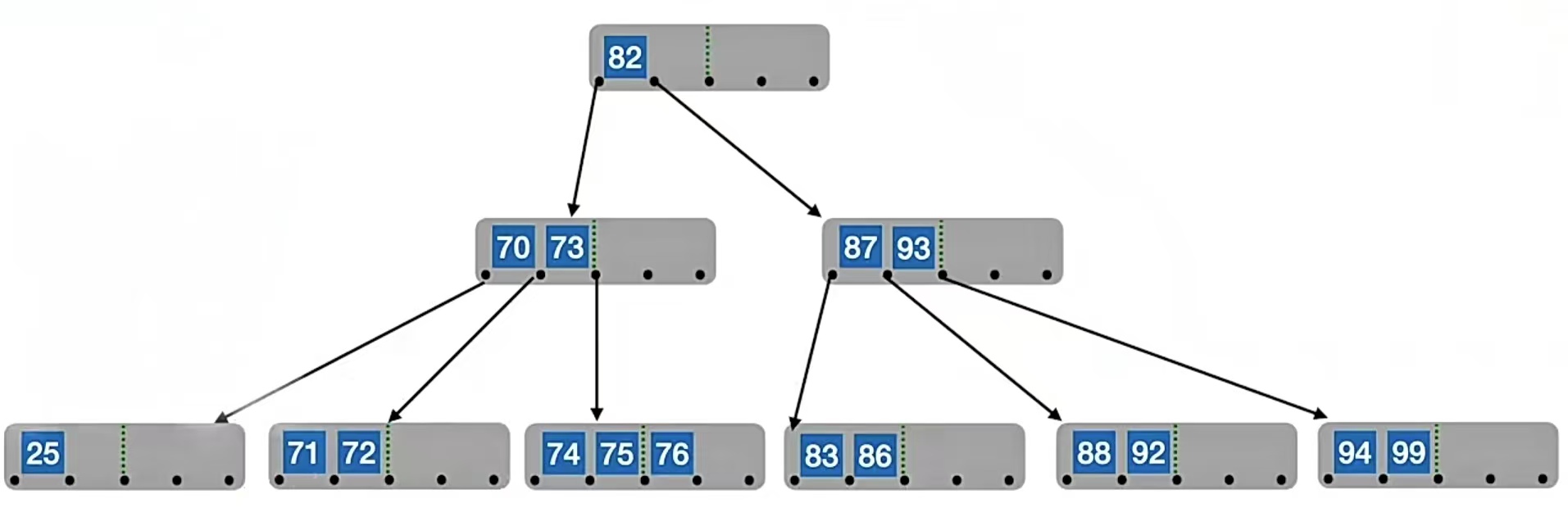
我们最左下那个结点中的关键字只有1个，个数低于下限 ⌈m/2⌉-1=2了。此时我们虽然内心很想借，但是也得别人借才行，别人自己都已经是最低下限了（右兄弟只有2个元素，要是被借走一个，那它就只剩1个元素了，就不满足个数不低于下限 ⌈m/2⌉-1=2了），你借了别人怎么办……所以这就是兄弟不够借的情况：

兄弟不够借。若被删除关键字所在结点删除前的关键字个数低于下限，且此时与该结点相邻的左、右兄弟结点的关键字个数均= ⌈m/2⌉-1，则将关键字删除后与左（或右）兄弟结点及双亲结点中的关键字进行合并

什么意思呢？我们的兄弟不够借，那合二为一好了，大家一起就不怕了，所以将关键字删除之后和兄弟合并。光合并兄弟可不行，因为被删除结点和兄弟结点头上的指针是不一样的（分别在父节点一个关键字的左右两侧），现在要合成一个了，头上的指针肯定也是一个，所以就把父结点中的关键字拉下水，一起合并，即把“25”和“71”、“72”合并，再把“70”合并进去：

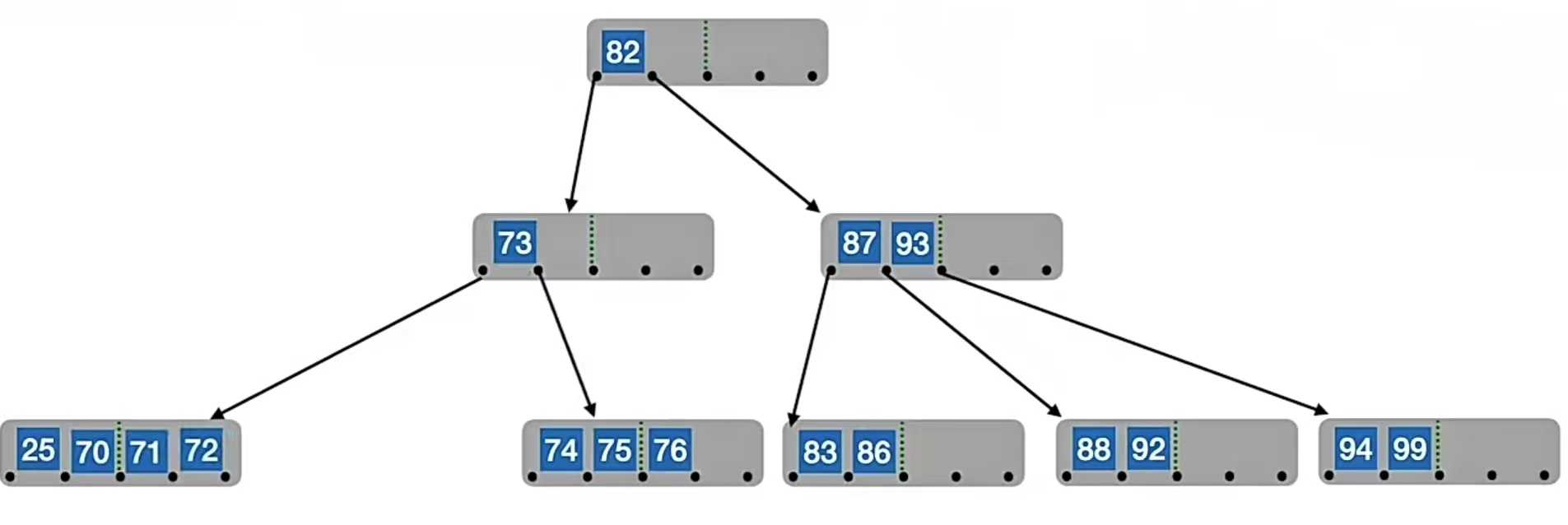
但是！！！！你有没有发现！！！这个时候它们的父结点里面关键字只有1个，个数低于下限 ⌈m/2⌉-1=2了。怎么办？没关系，别急，我们借一个就好了。不够借？也没关系，我们再再合并就好了。还记得我们怎么合并的吗？先和右兄弟合并，再把父结点中夹着的关键字拉下来一起合并，也就是把“73”和“87”、“93”合并，再把“82”合并进去：

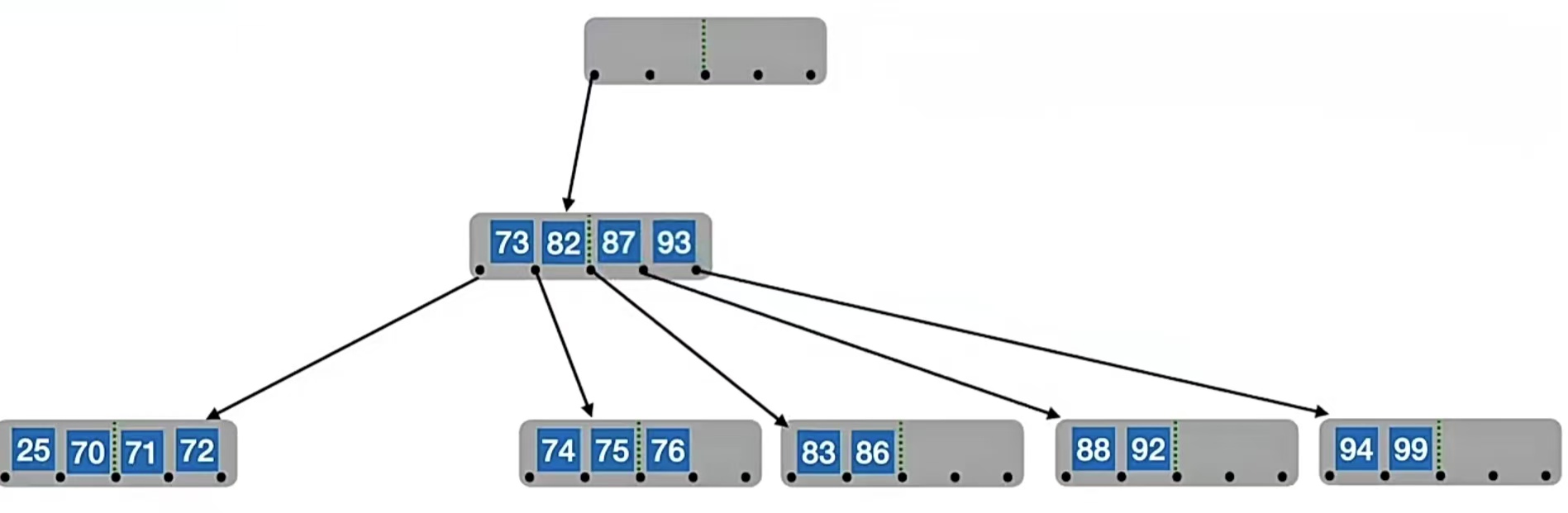
我们发现根节点关键字个数变为0了！怎么办？直接删除根结点，根结点中的元素被拉下来合并，那现在的合并的结点就变成根结点得了：

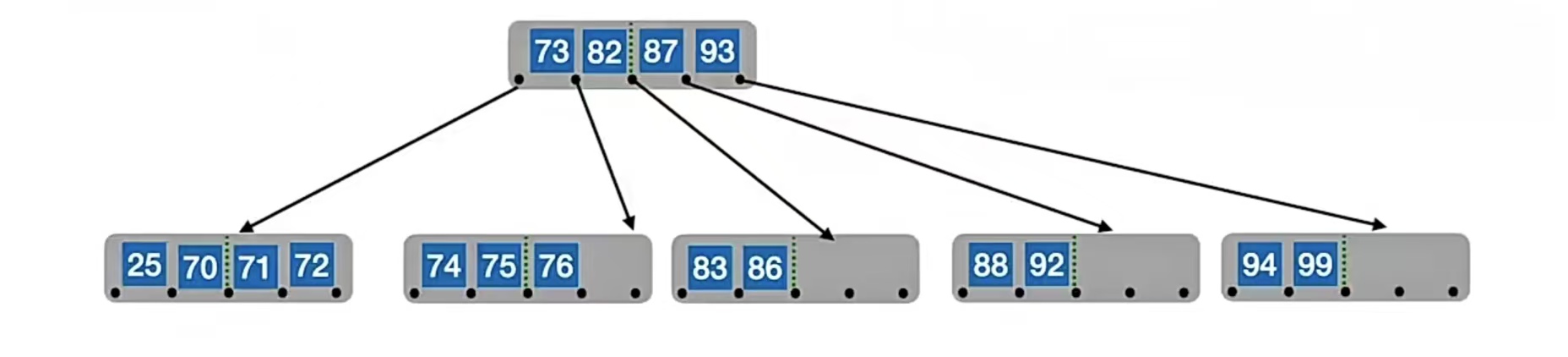
即在合并过程中，双亲结点中的关键字个数会减1。若其双亲结点是根结点且关键字个数减少至0（根结点关键字个数为1时，有2棵子树），则直接将根结点删除，合并后的新结点成为根；

若双亲结点不是根结点，且关键字个数减少到 ⌈m/2⌉-2，则又要与它自己的兄弟结点进行调整或合并操作，并重复上述步骤，直至符合B树的要求为止。

三、B+树

1.B+树

说完了B树，我们说说B+树。我们先来看一棵4阶B+树：

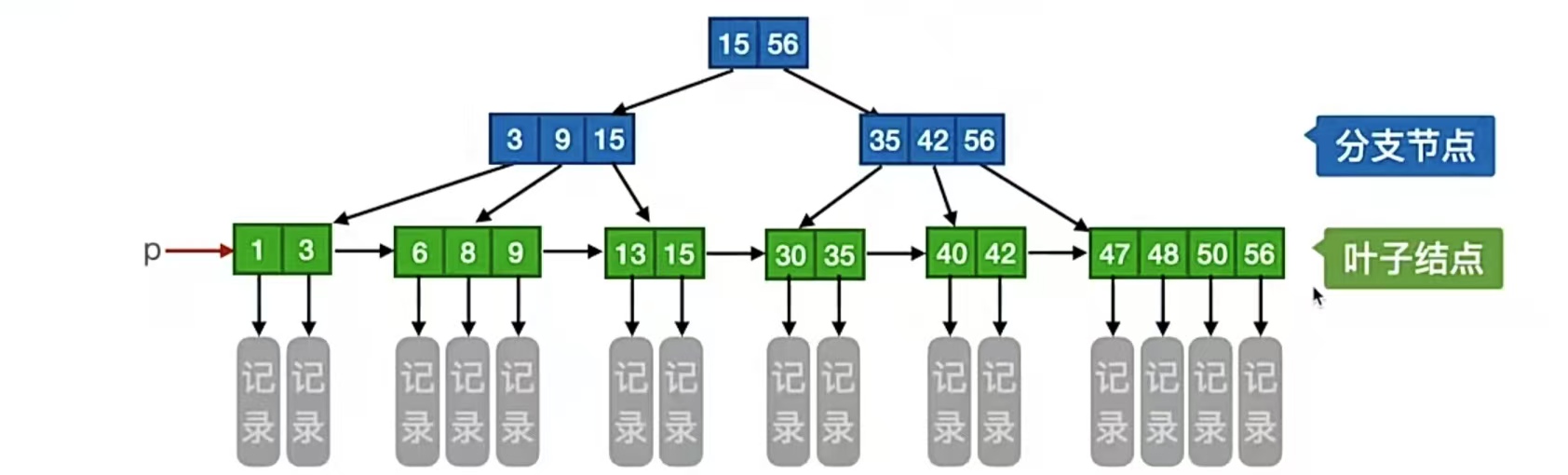
和B树还是很不一样呀。我们可以观察到，B+树中父节点保存的是子树中最大的那个元素，这是不是有点眼熟？分块查找是吧，块间有序，块内无序的那个分块查找，还记得吗？来回顾一下：

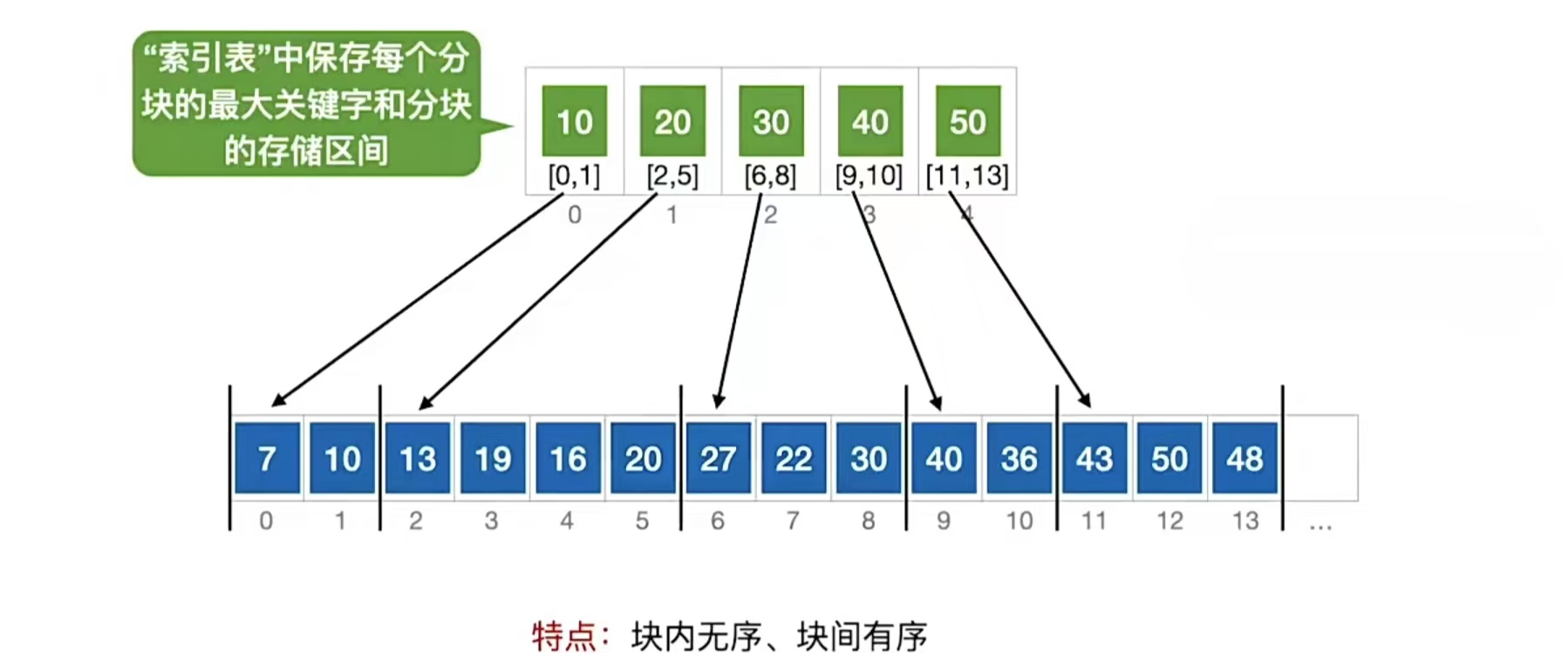
我们会发现，B+树和分块查找很像。但是也不是很像，因为分块查找没有那么多层，B+树有很多层。那么B+树的定义是什么呢？

一棵m阶的B+树需满足下列条件：

1. 每个分支结点最多有m棵子树（孩子结点）；
2. 非叶根结点至少有两棵子树，其他每个分支结点至少有 ⌈m/2⌉ 棵子树；
3. 结点的子树个数与关键字个数相等；
4. 所有叶结点包含全部关键字及相应记录的指针，叶结点中将关键字按大小顺序排列，并且相邻叶结点按大小顺序互相连接起来；
5. 所有分支结点中仅包含它的各个子结点中关键字的最大值及指向其子结点的指针。

我们仍然一条一条看。首先第1条很容易理解，毕竟m阶B+树，所以每个分支结点子树个数得不超过m；那么第2条呢？非叶根结点至少有两棵子树，非叶根节点就是 根节点不是叶子结点的情况，当根节点不是叶子结点（即至少有2层）的时候，至少有2棵子树（其实就是追求平衡），其他的时候每个分支结点至少有 ⌈m/2⌉ 棵子树。（其他时候不包括根节点是叶子结点的时候，比如3阶B+树中， ⌈m/2⌉ =2，根节点是叶子结点的时候，允许只有1个关键字，我觉得这里强调根节点非叶子结点的时候至少2个子树是为了强调平衡，不要因为概念去钻牛角尖。）

举个栗子，看下面的是不是B+树。左1只有1个根节点，根节点下方没有其他结点了，所以根节点是叶子结点，没有要求，是B+树；左2根节点不是叶子结点，所以它应该至少有2棵子树，但它只有1棵，所以不是B+树；右1根节点不是叶子结点，所以它也应该至少有2棵子树，它满足，其他每个分支结点至少有 ⌈m/2⌉ =2棵子树，所以是4阶B+树。

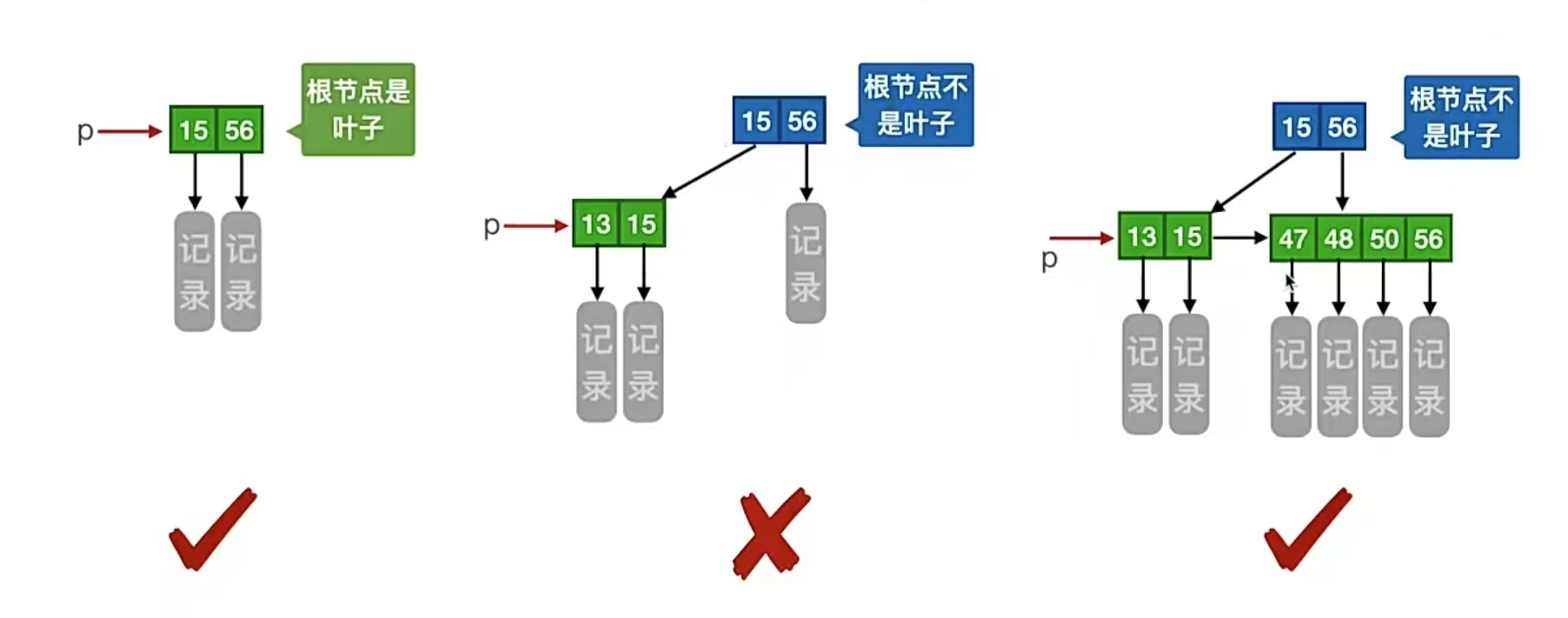
第3条，结点的子树个数与关键字个数相等，其实我们看那个4阶B+树就可以看出来，这和B树不一样，B树是在关键字的左右两边冒出来指针，我们的B+树是直接在关键字底下冒出来指针，这条主要说这个的。

第4条，很显然了这就，我们看这个4阶B+树的图，里面所有叶结点包含全部关键字及相应记录的指针，叶结点中将关键字按大小顺序排列，并且相邻叶结点按大小顺序互相连接起来（这说明它支持顺序查找），这个没什么说的。

第5条，我们看图就会发现，除了p指针指向的绿色的结点，其他上面层里面的关键字都是绿色层出现过的，且指向它们的那个结点存放的是它们中的最大值，所以所有分支结中仅包含它的各个子结点中关键字的最大值及指向其子结点的指针。

2.B+树的查找

B+树中，无论查找成功与否，最终一定都要走到最下面一层结点

因为B+树上面层的都是最底下一层的重复数据，就算查找成功，也得到最下面一层才能看记录，查找失败也得到最下面那一层才知道（因为存放的是最下面一层的结点最大值，得到最下面那一层才知道到底有没有）。

比如我们要在上面那个4阶B+树中查找“9”，先看根节点，9<15，所以在“15”指向的那个结点里面找。3<9,9=9，所以在“9”指向的那个结点里面找。6<9，8<9，9=9，查找成功，9指向的“记录”就是我们要找到内容。（当然也可以p指针顺序查找。）

那B树的查找呢？也是必须落到最下面那一层吗？no no no，我们的B树不一样，查找成功，可能停在任意一层，比如下面这张图：

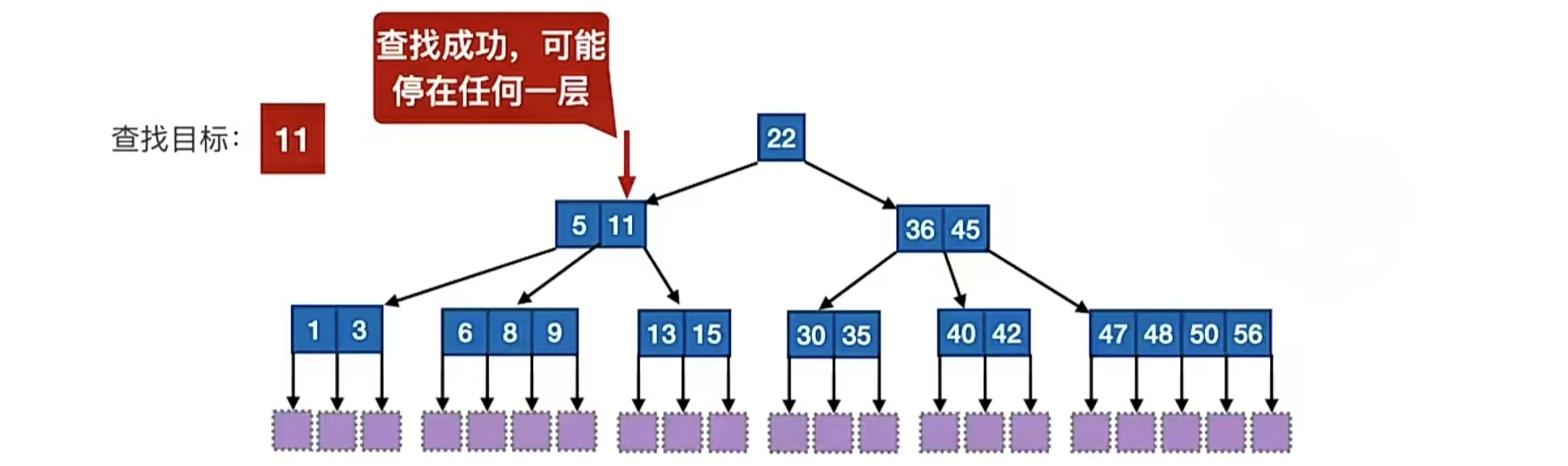
查找失败才落到叶子结点上。

3.B树和B+树的区别

• B树结点中n个关键字对应n+1棵子树，B+树结点中的n个关键字对应n棵子树；

• B树根结点中的关键字数 n ∈ [1,m-1]，其他结点的关键字数 n ∈ [ ⌈m/2⌉,m-1]；B+树根结点中的关键字数 n ∈ [1,m]，其他结点的关键字数 n ∈ [ ⌈m/2⌉,m]（都是最多m个分支）

• B树中，各结点中包含的关键字是不重复的；在B+树中，叶结点包含全部关键字，非叶结点中出现过的关键字也会出现在叶结点中（叶结点是指绿色的那个最下面层的哈）

• B树的结点中都包含了关键字对应的记录的存储地址；在B+树中，叶结点包含信息，所有非叶结点仅起索引作用，非叶结点中的每个索引项只含有对应子树的最大关键字和指向该子树的指针，不含有该关键字对应记录的存储地址

  • 其实就是B树中非叶结点是有信息的，B+树中非叶结点是没信息的。

在B+树中，非叶结点不含有该关键字对应记录的存储地址,可以使一个磁盘块能包含更多个关键字，使得B+树的阶更大，树高更矮，读磁盘数更少，查找更快。

为啥读磁盘数更少？因为我们B+树每个结点都存放在各个磁盘块里，每次拿数据都要把磁盘块读到内存中，这个操作很耗时，当我们非叶结点不存其他东西，只存索引，那就可以放更多索引，树高就变得更矮，往下找的时候需要读的磁盘数（层数）就更少，这样就快了。

典型应用：关系型数据库的“索引”（如MySQL）

回顾小总结一下：

	m阶B树	m阶B+树
类比	二叉查找树的进化 ——> m叉查找树	分块查找的进化——>多级分块查找
关键字与分叉	n 个关键字对应 n+1 个分叉（子树）	n个关键字对应n个分叉
结点包含的信息	所有结点中都包含记录的信息	只有最下层叶子结点才包含记录的信息（可使树更矮）
查找方式	不支持顺序查找。查找成功时，可能停在任何一层结点，查找速度“不稳定”	支持顺序查找。查找成功或失败都会到达最下一层结点，查找速度“稳定”

	m阶B树 、m阶B+树
相同点	除根节点外，最少 ⌈m/2⌉ 个分叉（确保结点不要太“空”）；任何一个结点的子树都要一样高（确保“绝对平衡”）

---

总结

B树的插入其实就是先找，找要插到哪（注意得是终端结点），完了再看看是不是“冒了”，“冒了”就分裂，把中间位置⌈m/2⌉的元素挤到上面去，挤到上面去还“冒了”就继续分裂；B树的删除就是看满不满足结点关键字个数不低于下限 ⌈m/2⌉-1，如果不满足，那就问兄弟借；如果够借，就用前驱，前驱的前驱（或后继，后继的后继）填补，如果不够借，就和兄弟合并，再把父结点中左右指针合并的那个元素拉下来。

B+树和B树的区别主要是B树是关键字左右开叉，B+树关键字就直接出叉；还有就是B+树中最底下一层包含所有关键字，其他上面层全是重复的，B树就不这样，每个关键字都不重复；B树中非叶结点有信息，B+树非叶结点只起索引作用。