当前位置： 首页 > news >正文

数据结构—排序(斐波那契数列，冒泡，选择，插入，快速，归并，图，广度优先算法)

news 来源：原创 2025/5/16 10:46:50

目录

一 斐波那契数列（递归算法）

定义

原理

二 冒泡排序

 定义

排序思路

函数原型

参数详解：

算法分析：

 1. 使用函数库的qsort函数

 2. 自定义冒泡排序

三 选择排序

定义

排序思路

四 插入排序

定义

排序思路

五 快速排序

定义

排序思路

六 归并排序

定义

排序思路

详细排序思路：

详细过程思路：

排序思路

七 广度优先算法

1. 定义

1. 是什么？

2. 为什么要学BFS？

2. BFS的详细思路与过程

1. 核心数据结构：队列（Queue）

2. 算法步骤分解（以树为例）

步骤1：初始化

步骤2：处理队列中的节点

步骤3：继续处理队列

步骤4：重复直到队列为空

八 图

一、图的定义

🌰 类比举例：

二、图的组成与关键术语

1. 图的分类

2. 核心术语

三、图的存储方式

1. 邻接矩阵（Adjacency Matrix）

2. 邻接表（Adjacency List）

四、图的遍历算法

1. 深度优先搜索（DFS, Depth-First Search）

2. 广度优先搜索（BFS, Breadth-First Search）

五、图的应用场景

六、代码实战：图的完整实现（邻接表）

七、总结

九 总结

一 斐波那契数列（递归算法）

定义

斐波那契数列是一个自然数序列，从0和1开始，后续每个数都是前两个数之和：

F(0)=0,F(1)=1,F(n)=F(n−1)+F(n−2)(n≥2)F(0)=0,F(1)=1,F(n)=F(n−1)+F(n−2)(n≥2)

原理

  • 递归思想：将问题分解为更小的同类问题。

  • 动态规划优化：避免重复计算，提高效率。

#include <stdio.h>
#include <stdlib.h>
/*
斐波那契数列（Fibonacci sequence），又称黄金分割数列 [1]，
因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称“兔子数列”，
其数值为：0、1、1、2、3、5、8、13、21、34……
在数学上，这一数列以如下递推的方法定义：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）。
*/
//使用递归算法，实现斐波那契数列（Fibonacci sequence）
int fibonacci(int n);int main(int argc, char const *argv[])
{//打印斐波那契数列（Fibonacci sequence）printf("请输入需要打印de斐波那契数列（Fibonacci sequence）数量(正整数)：\n");int n;scanf("%d",&n);printf("斐波那契数列（Fibonacci sequence）:\n");for (int i = 0; i < n; i++){printf("%d ",fibonacci(i));}printf("\n");return 0;
}//使用递归算法，实现斐波那契数列（Fibonacci sequence）
int fibonacci(int n){if (n<0){printf("斐波那契数列没有负数....\n");exit(EXIT_FAILURE);//异常退出}else if (n<=1){return n;//结束条件}else{//递归调用自身，实现实现斐波那契数列（Fibonacci sequence）return fibonacci(n-1)+fibonacci(n-2);}}

二 冒泡排序

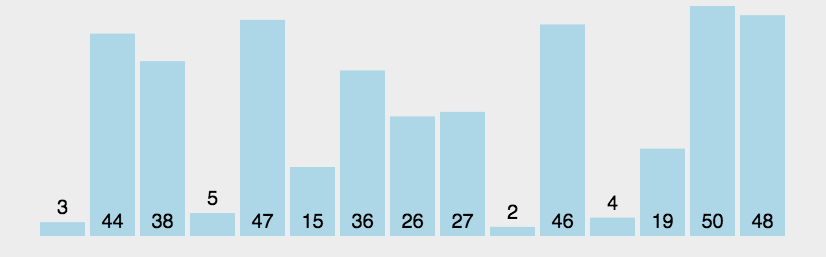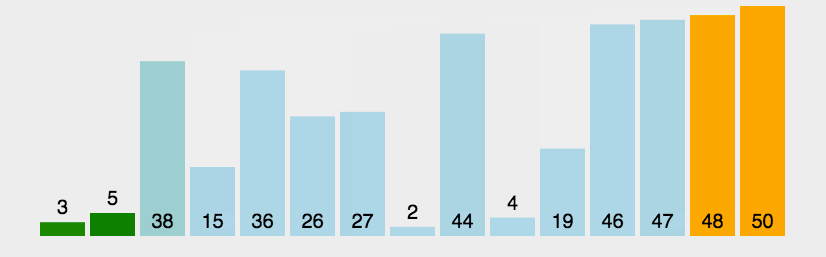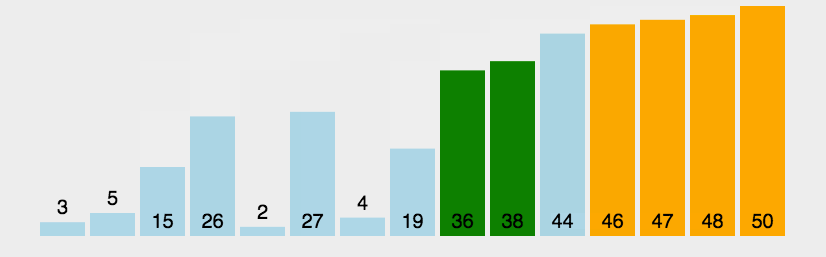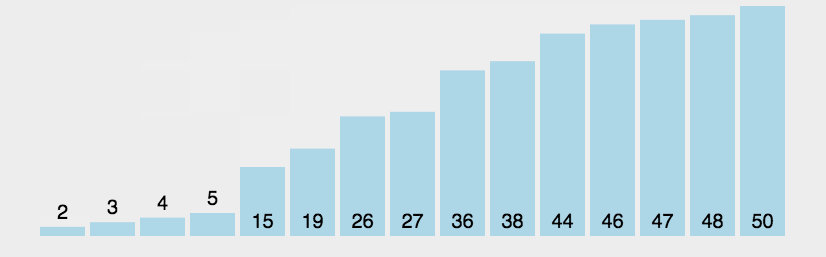
java 冒泡排序 包括（超级简单，简单，一般）_java冒泡排序-CSDN博客

java的冒泡排序

冒泡排序：
    一种排序的方式，对要进行排序的数据中相邻的数据进行两两比较，将较大的数据放在后面，依次对所有的数据进行操作，直至所有的数据按照要求完成排序.

 定义

通过重复交换相邻的逆序元素，将最大元素逐步“冒泡”到数组末尾。头文件：stdlib.h

排序思路

  1. 外层循环：控制遍历轮数（每轮确定一个最大元素的位置）。

  2. 内层循环：遍历未排序部分，比较相邻元素并交换。

  3. 外层循环控制需要进行的排序轮数，每轮将最大的元素“冒泡”到数组的末尾；

  4. 内存循环则负责逐个比较相邻的元素，并在必要时交换它们的位置；

  5. 每次循环将最大的元素移动到右侧，直到整个数组排序完成

函数原型

void qsort(void *base, size_t nitems, size_t size, int (*compar)(const void *, const void *)
);

参数详解：

参数名类型描述
basevoid*指向待排序数组首元素的指针。
nitemssize_t数组中待排序的元素数量。
sizesize_t每个元素的大小（字节数），通常用 sizeof(元素类型) 获取。
comparint (*)(const void*, const void*)比较函数指针，需自定义逻辑：
- 返回值 <0：第一个元素较小；
- 返回值 =0：两元素相等；
- 返回值 >0：第一个元素较大。

算法分析：

   时间复杂度：

        最好情况：O(n^2)
       最坏情况：O(n^2)
       平均情况：O(n^2)
    空间复杂度：只有一个额外变量
        最好情况：O(1)
        最坏情况：O(1)
        平均情况：O(1)
    稳定性（相等元素的顺序）:冒泡排序是稳定的排序算法，相等元素不会被打乱顺序
    尽管冒泡排序简单易懂，但是效率低下，通常不适用于大规模数据的排序

 1. 使用函数库的qsort函数

#include <stdio.h>
#include <stdlib.h>
/*
二、C语言有自有的qsort函数。
头文件：stdlib.h
原型： void qsort(void *base, size_t nitems, size_t size, int (*compar)(const void *, const void *));参数：1. void *_Basebase: 指向待排序数组的第一个元素的指针。2. size_t _NumOfElements数组中的元素数量。3. size_t _SizeOfElements数组中每个元素的大小（以字节为单位）。4.int(__cdecl * _PtFuncCompare)(const void *, const void *)compar: 比较函数的指针，该函数用于比较两个元素。比较函数应当返回一个整数，表示比较结果：小于零：表示第一个元素小于第二个元素。等于零：表示两个元素相等。大于零：表示第一个元素大于第二个元素。5.无返回值
*/
// 定义一个包含五个整数的数组
int values[] = {88, 56, 100, 2, 25};// 比较函数，用于比较两个整数，返回值为两值之差
int cmpfunc(const void *a, const void *b)
{return (*(int *)a - *(int *)b);
}int main()
{int n;// 输出排序之前的数组内容printf("排序之前的列表：\n");// 遍历输出values的值，此处使用的是int n 我认为不妥，应该define一个自动长度for (n = 0; n < 5; n++){printf("%d ", values[n]);}// qsort其实是在库中声名的一个函数，并没有定义其内容// 使用 qsort 函数对数组进行排序qsort(values, 5, sizeof(int), cmpfunc);// 输出排序之后的数组内容printf("\n排序之后的列表：\n");for (n = 0; n < 5; n++){printf("%d ", values[n]);}return 0;
}
/*
GitHub Copilot:你的观察是正确的：在 stdlib.h 头文件中，qsort 只是进行了声明（即函数原型），并没有给出具体的实现（定义）。例如：为什么你能直接调用 qsort？
这是因为：声明告诉编译器有这样一个函数，参数和返回值是什么。
定义（实现）实际代码并不在头文件里，而是在对应的C标准库实现（如 Windows 下的 msvcrt.dll 或 ucrtbase.dll，Linux 下的 libc.so）的源代码中。
链接时，编译器会把你的 qsort 调用链接到C运行库（CRT）中已经实现好的 qsort 函数。
具体实现在哪里？
在 Windows 下，qsort 的实现通常在 msvcrt.dll 或 ucrtbase.dll 这样的动态链接库（DLL）里。
你用 MinGW 或 MSVC 编译时，链接器会自动把你的程序和这些库链接起来。
你可以在 MinGW 的源码包或微软的 CRT 源码中找到 qsort 的具体实现（如 qsort.c），但普通用户只需要声明和链接库即可使用。
总结
头文件只声明了 qsort，没有实现。
实现代码在C运行库的源代码或二进制库（DLL、.lib等）中。
链接器负责把你的调用和库里的实现关联起来，所以你能直接用。
如果你想看具体实现，可以去查找 MinGW 或 MSVC 的 CRT 源码包，搜索 qsort.c 文件。
*/

 2. 自定义冒泡排序

#include <stdio.h>
#define LENGTH(array) (sizeof(array)/sizeof(array[0]))/*
冒泡排序：冒泡排序是一种简单的排序算法，它重复地遍历待排序的列表，一次比较两个相邻的元素，如果它们的顺序错误(从小到大/从大到小)就把它们交换过来；实现：
1.外层循环控制需要进行的排序轮数，每轮将最大的元素“冒泡”到数组的末尾；
2.内存循环则负责逐个比较相邻的元素，并在必要时交换它们的位置；
3.每次循环将最大的元素移动到右侧，直到整个数组排序完成算法分析：时间复杂度： 最好情况：O(n^2)最坏情况：O(n^2)平均情况：O(n^2)空间复杂度：只有一个额外变量最好情况：O(1)最坏情况：O(1)平均情况：O(1)稳定性（相等元素的顺序）:冒泡排序是稳定的排序算法，相等元素不会被打乱顺序尽管冒泡排序简单易懂，但是效率低下，通常不适用于大规模数据的排序*///冒泡排序
void bubble_sort(int arr[],int n);//打印数组
void print_array(int arr[],int n);int main(int argc, char const *argv[])
{int arr[]={66,77,88,41,11,1,2,5,3,69,7,4,6,6,9,65,5,65,66,5};printf("排序前：\n");print_array(arr,LENGTH(arr));printf("bubble_sort 冒泡排序：\n");bubble_sort(arr,LENGTH(arr));printf("排序后：\n");print_array(arr,LENGTH(arr));return 0;
}//冒泡排序
void bubble_sort(int arr[],int n){//三个临时变量int i,j,temp;//1.外层循环控制需要进行的排序轮数，每轮将最大的元素“冒泡”到数组的末尾；for ( i = 0; i < n-1; i++){//2.内存循环则负责逐个比较相邻的元素，并在必要时交换它们的位置；for ( j = 0; j < n-1-i; j++){//3.每次循环将最大的元素移动到右侧，直到整个数组排序完成if (arr[j]>arr[j+1]){temp=arr[j];arr[j]=arr[j+1];arr[j+1]=temp;}}}
}//打印数组
void print_array(int arr[],int n){for (int i = 0; i < n; i++){printf("%d ",arr[i]);}printf("\n");
}

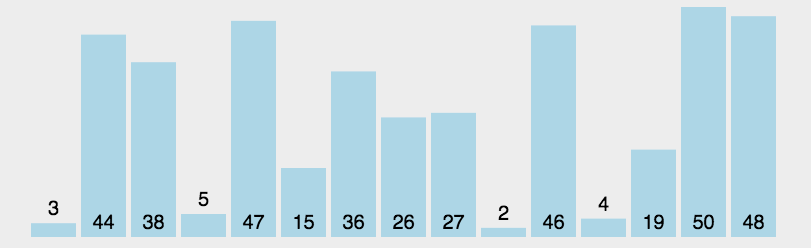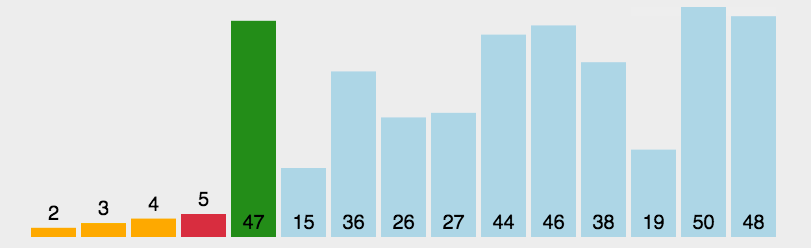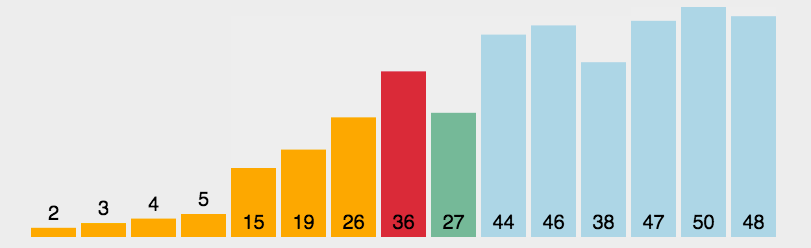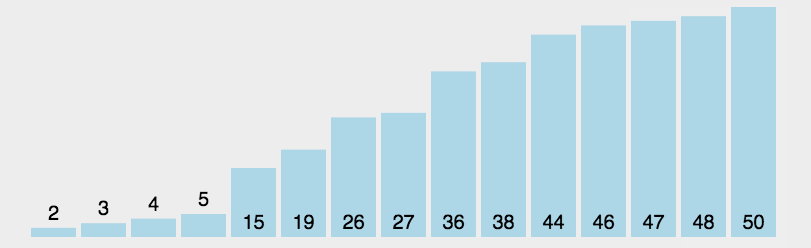
三 选择排序

定义

首先，在待排序序列中定位最小（或最大）元素，将其与序列首元素交换位置；随后，在剩余未排序元素中继续寻找最小（或最大）元素，并与未排序部分的首元素交换。这一过程循环进行，直至所有元素有序排列。

在每次迭代中，算法都会确定未排序部分的最小（或最大）元素，并将其添加到已排序序列的末尾，从而逐步构建有序序列。

排序思路

  1. 外层循环：遍历数组，确定当前位置应放置的最小元素。

  2. 内层循环：在未排序部分中找到最小值索引。

  3. 交换：将最小值与当前位置元素交换。

#include <stdio.h>
#define LENGTH(array) (sizeof(array)/sizeof(array[0]))/*
选择排序：选择排序是一种简单直观的排序算法，它首先在待排序序列中找到最小(最大)元素，然后将其放置在已排序序列的末尾，然后再从剩余未排序元素中继续选择最小(或最大)元素，依次类推，直到所有元素都排序完成。每次循环会找到未排序部分最小(最大)元素，放到已排序部分的末尾；实现：1.外层循环控制待排序部分的起始位置2.内层循环直到未排序部分最小元素(或者最大)的位置min_index3.找到最小元素后，将其与当前未排序部分的第一个元素交换算法分析：时间复杂度： 最好情况：O(n^2)最坏情况：O(n^2)平均情况：O(n^2)空间复杂度：只有一个额外变量最好情况：O(1)最坏情况：O(1)平均情况：O(1)稳定性（相等元素的顺序）:选择排序是不稳定的排序算法，相等元素会被打乱顺序尽管选择排序简单易懂，但是效率低下，通常不适用于大规模数据的排序*///打印数组
void print_array(int arr[],int n);//选择排序
void selection_sort(int arr[],int n);int main(int argc, char const *argv[])
{int arr[]={66,77,88,41,11,1,2,5,3,69,7,4,6,6,9,65,5,65,66,5};printf("排序前：\n");print_array(arr,LENGTH(arr));printf("selection_sort 选择排序：\n");selection_sort(arr,LENGTH(arr));printf("排序后：\n");print_array(arr,LENGTH(arr));return 0;
}//打印数组
void print_array(int arr[],int n){for (int i = 0; i < n; i++){printf("%d ",arr[i]);}printf("\n");
}//选择排序
void selection_sort(int arr[],int n){int i,j,min_index,temp;for ( i = 0; i < n-1; i++){//找到未排序部分最小的元素//假如待排序第一个是最小的min_index=i;for ( j = i+1; j < n; j++){if (arr[j]<arr[min_index]){min_index=j;}}//循环结束，找到当前轮最小的index//找到最小元素后，将其与当前未排序部分的第一个元素交换temp=arr[min_index];arr[min_index]=arr[i];arr[i]=temp;}
}

四 插入排序

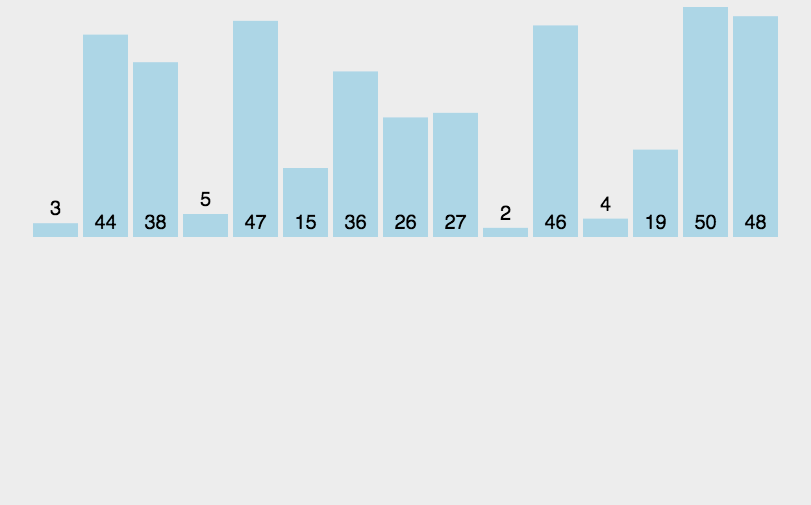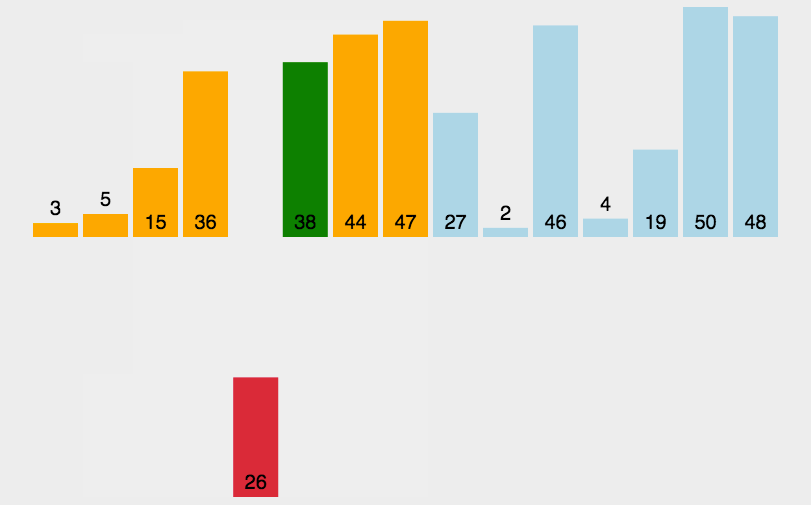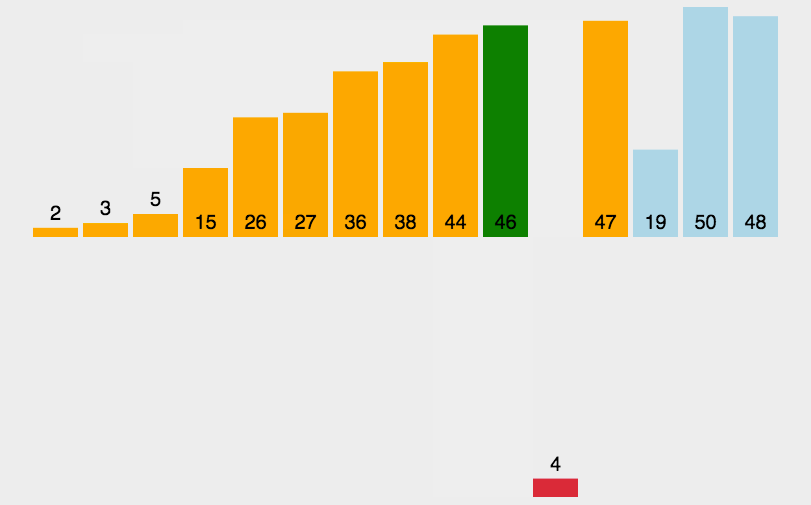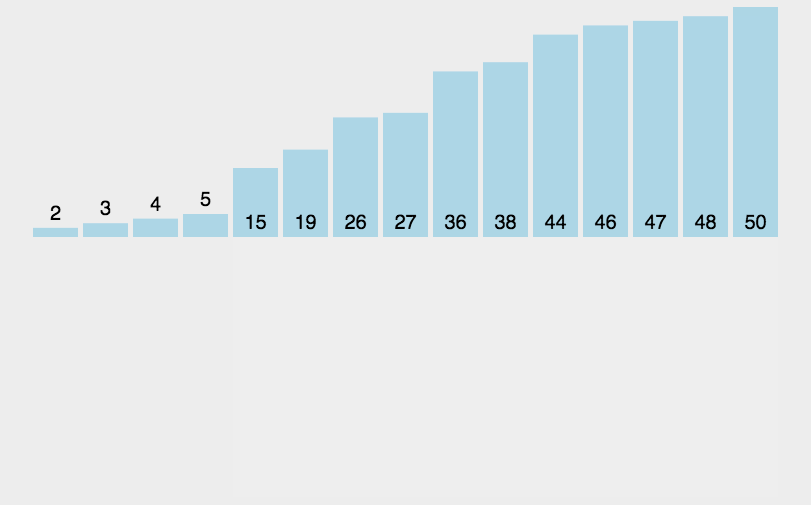
插入排序：

    插入排序是一种简单直观的排序算法，它的工作方式类似于按顺序将扑克牌插入到手中的牌中。

    插入排序每次从未排序部分取出一个元素，将它插入已排序部分的正确位置。

    每次循环将未排序部分的第一个元素插入到已排序部分的正确位置，直到整个数组排序完成。

定义

将未排序元素逐个插入到已排序部分的正确位置。

排序思路

  1. 外层循环：遍历未排序元素（从第二个元素开始）。

  2. 内层循环：将当前元素与已排序部分从后向前比较，找到插入位置。

 

#include <stdio.h>#define LENGTH(array) (sizeof(array)/sizeof(array[0]))/*
插入排序：插入排序是一种简单直观的排序算法，它的工作方式类似于按顺序将扑克牌插入到手中的牌中。插入排序每次从未排序部分取出一个元素，将它插入已排序部分的正确位置。每次循环将未排序部分的第一个元素插入到已排序部分的正确位置，直到整个数组排序完成。插入排序的实现：
1.外层循环从第二个元素开始(即index为1)，将每个元素插入到前面已排序的部分中
2.内层循环将当前元素与前面已排序部分的元素进行比较，并将比当前元素大的元素后移一位，直到找到合适的位置插入当前元素算法分析：时间复杂度： 最好情况：O(n^2)最坏情况：O(n^2)平均情况：O(n^2)空间复杂度：只有一个额外变量最好情况：O(1)最坏情况：O(1)平均情况：O(1)稳定性（相等元素的顺序）:插入排序是稳定的排序算法，相等元素不会被打乱顺序尽管插入排序简单易懂，但是效率低下，通常不适用于大规模数据的排序
*///插入排序
void insertion_sort(int arr[],int n);//打印数组
void print_array(int arr[],int n);int main(int argc, char const *argv[])
{int arr[]={66,77,88,41,11,1,2,5,3,69,7,4,6,6,9,65,5,65,66,5};printf("排序前：\n");print_array(arr,LENGTH(arr));printf("insertion_sort 插入排序：\n");insertion_sort(arr,LENGTH(arr));printf("排序后：\n");print_array(arr,LENGTH(arr));return 0;
}//打印数组
void print_array(int arr[],int n){for (int i = 0; i < n; i++){printf("%d ",arr[i]);}printf("\n");
}//插入排序
void insertion_sort(int arr[],int n){int i,j,key;//1.外层循环从第二个元素开始(即index为1)，将每个元素插入到前面已排序的部分中for ( i = 1; i < n; i++){key=arr[i];j=i-1;//2.内层循环将当前元素与前面已排序部分的元素进行比较，并将比当前元素大的元素后移一位，直到找到合适的位置插入当前元素while (j>=0 && arr[j]>key){arr[j+1]=arr[j];j--;}//找到合适的位置插入当前元素arr[j+1]=key;}
}

五 快速排序

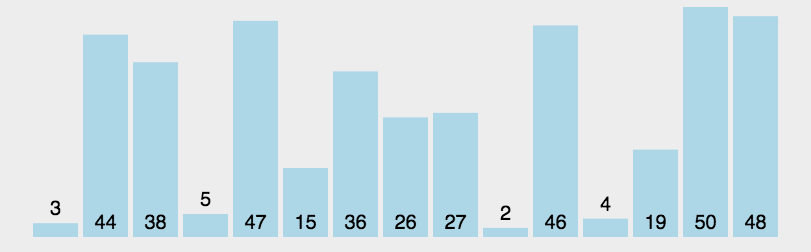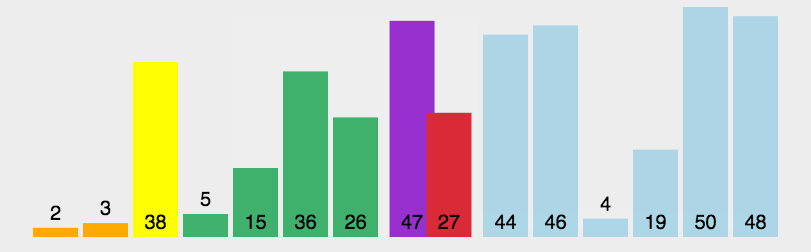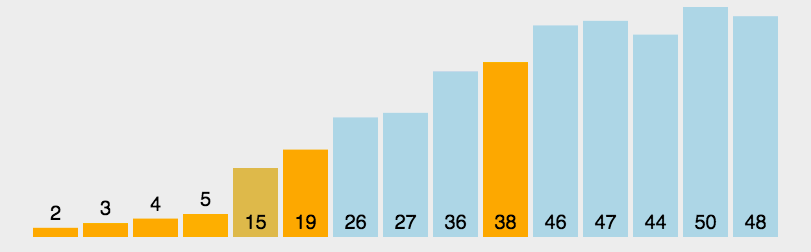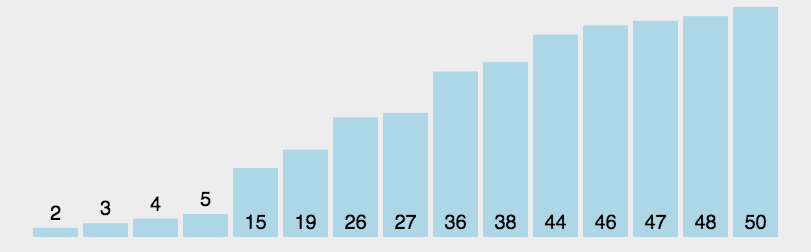
快速排序：

    快速排序是一种分治算法。它选择一个元素作为“枢轴”(pivot),

    将数组分成两部分，小于枢轴的元素放在枢轴的左边，大于枢轴的元素放在枢轴的右边，

    然后对两部分递归进行快速排序。

定义

采用分治策略，选择一个基准元素，将数组分为左右两部分（左半部分≤基准，右半部分≥基准），递归排序子数组。

排序思路

  1. 基准选择：通常选第一个或中间元素。

  2. 分区操作：将数组分为左右两部分。

  3. 递归排序：对左右子数组重复上述步骤。

#include <stdio.h>
#include <stdlib.h>
int main(int argc, char const *argv[])
{// 1. 首先，我们需要一个快速排序的函数声明void quick_sort(int arr[], int left, int right);// 2. 还需要一个打印数组的函数声明，方便观察排序前后的结果void print_array(int arr[], int size);// 3. 定义一个待排序的数组int arr[] = {34, 7, 23, 32, 5, 62, 32, 2, 78, 1};int n = sizeof(arr) / sizeof(arr[0]); // 计算数组长度// 4. 打印排序前的数组printf("排序前的数组: ");print_array(arr, n);// 5. 调用快速排序函数，对整个数组进行排序quick_sort(arr, 0, n - 1);// 6. 打印排序后的数组printf("排序后的数组: ");print_array(arr, n);return 0;
}// 快速排序的实现
//  参数说明：arr为待排序数组，left为排序区间左端点，right为右端点
void quick_sort(int arr[], int left, int right)
{// 递归终止条件：当区间内只有一个或没有元素时，直接返回if (left >= right){return;}// 选择基准值，这里选择区间最左边的元素int pivot = arr[left];int i = left;int j = right;// 下面进行一趟排序，将比pivot小的放左边，大的放右边while (i < j){// 从右往左找第一个小于pivot的元素while (i < j && arr[j] >= pivot){j--;}if (i < j){arr[i] = arr[j]; // 将小于pivot的元素填到左边的坑i++;}// 从左往右找第一个大于pivot的元素while (i < j && arr[i] <= pivot){i++;}if (i < j){arr[j] = arr[i]; // 将大于pivot的元素填到右边的坑j--;}}// 最后将基准值归位arr[i] = pivot;// 递归排序基准值左边和右边的子区间quick_sort(arr, left, i - 1);quick_sort(arr, i + 1, right);
}// 打印数组的函数实现
void print_array(int arr[], int size)
{for (int i = 0; i < size; i++){printf("%d ", arr[i]);}printf("\n");
}

六 归并排序

定义

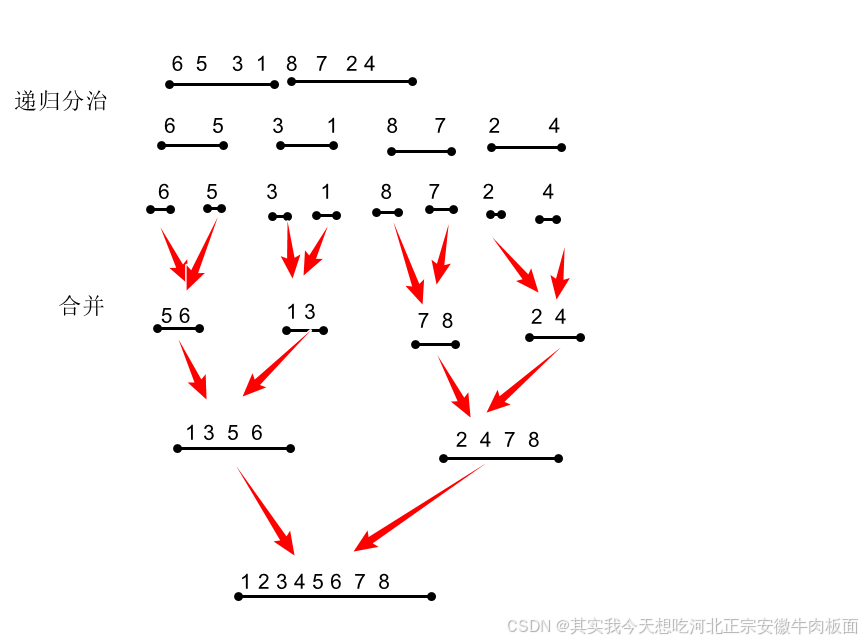
采用分治策略，将数组递归分为两半，分别排序后合并。然后将排好序的子数组合并成一个有序的大数组。

排序思路

  1. 分解：将数组递归分为两半，直到子数组长度为1。

  2. 合并：将两个有序子数组合并为一个有序数组。

详细排序思路：

1. 如果数组长度为1，说明已经有序，直接返回。

2. 将数组从中间分成左右两个部分。

3. 对左半部分递归进行归并排序。

4. 对右半部分递归进行归并排序。

5. 合并两个有序的子数组，得到一个有序的大数组。

详细过程思路：

排序思路

  1. 分解：将数组递归分为两半，直到子数组长度为1。

  2. 合并：将两个有序子数组合并为一个有序数组。

  3. 递归拆分：不断将数组对半分，直到每个子数组只剩下一个元素。

  4. 合并过程：将两个有序的子数组合并成一个有序数组。合并时，分别用指针指向两个子数组的起始位置，比较指针所指元素的大小，将较小的元素放入临时数组，然后指针后移，直到有一个子数组元素全部放入临时数组，再将另一个子数组剩余的元素全部放入临时数组。

  5. 最后将临时数组的内容复制回原数组。

#include <stdio.h>
#include <stdlib.h>
#define LENGTH(array) (sizeof(array) / sizeof(array[0]))/*
/*
归并排序（Merge Sort）是一种分治法（Divide and Conquer）的典型应用。
它的基本思想是：将一个大的无序数组递归地分成两个子数组，分别对这两个子数组进行排序，
然后将排好序的子数组合并成一个有序的大数组。详细排序思路：
1. 如果数组长度为1，说明已经有序，直接返回。
2. 将数组从中间分成左右两个部分。
3. 对左半部分递归进行归并排序。
4. 对右半部分递归进行归并排序。
5. 合并两个有序的子数组，得到一个有序的大数组。详细过程思路：
- 递归拆分：不断将数组对半分，直到每个子数组只剩下一个元素。
- 合并过程：将两个有序的子数组合并成一个有序数组。合并时，分别用指针指向两个子数组的起始位置，比较指针所指元素的大小，将较小的元素放入临时数组，然后指针后移，直到有一个子数组元素全部放入临时数组，再将另一个子数组剩余的元素全部放入临时数组。
- 最后将临时数组的内容复制回原数组。代码实现如下：
*/// 合并两个有序子数组的函数
void merge(int arr[], int left, int mid, int right)
{int n1 = mid - left + 1; // 左子数组长度int n2 = right - mid;    // 右子数组长度// 创建临时数组int *L = (int *)malloc(n1 * sizeof(int));int *R = (int *)malloc(n2 * sizeof(int));// 拷贝数据到临时数组L和Rfor (int i = 0; i < n1; i++)L[i] = arr[left + i];for (int j = 0; j < n2; j++)R[j] = arr[mid + 1 + j];// 合并临时数组到原数组arrint i = 0, j = 0, k = left;while (i < n1 && j < n2){if (L[i] <= R[j]){arr[k++] = L[i++];}else{arr[k++] = R[j++];}}// 将L剩余元素复制到arrwhile (i < n1){arr[k++] = L[i++];}// 将R剩余元素复制到arrwhile (j < n2){arr[k++] = R[j++];}// 释放临时数组free(L);free(R);
}// 归并排序的递归函数
void mergeSort(int arr[], int left, int right)
{if (left < right){int mid = left + (right - left) / 2; // 防止溢出// 对左半部分排序mergeSort(arr, left, mid);// 对右半部分排序mergeSort(arr, mid + 1, right);// 合并两个有序子数组merge(arr, left, mid, right);}
}
int main(int argc, char const *argv[])
{int a[] = {5, 9, 55, 48, 6, 226, 48, 2, 3, 6, 4, 959, 262};// 数组a的长度int n = LENGTH(a);printf("排序前: ");// 遍历一下原数组for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");// 调用归并排序// 0 表示数组的起始下标// n-1 表示数组的结束下标（最后一个元素）// 这样可以让归并排序处理整个数组mergeSort(a, 0, n - 1);printf("排序后: ");for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");return 0;
}

七 广度优先算法

1. 定义

1. 是什么？

  • 广度优先算法是一种用于遍历或搜索树（Tree）或图（Graph）的算法。

  • 核心思想：逐层访问节点，先访问离起点最近的节点，再访问更远的节点。

  • 类比理解：像“水波纹扩散”一样，从起点开始，一圈一圈向外探索。

2. 为什么要学BFS？

  • 解决最短路径问题（如迷宫最短出口）。

  • 社交网络中查找“二度人脉”。

  • 网络爬虫按层级抓取网页。

2. BFS的详细思路与过程

1. 核心数据结构：队列（Queue）

  • 队列特性：先进先出（FIFO），保证按层级顺序处理节点。

  • 操作：

    • 入队（Enqueue）：将未访问的相邻节点加入队列。

    • 出队（Dequeue）：处理当前节点。

2. 算法步骤分解（以树为例）

假设有一棵树如下：

        A/ \B   C/ \   \D   E   F
步骤1：初始化

  • 创建一个空队列。

  • 将起点（根节点A）标记为已访问并入队。

队列：[A]
已访问：{A}
步骤2：处理队列中的节点

  • 出队A，打印A。

  • 访问A的子节点B和C，标记为已访问并入队。

队列：[B, C]
已访问：{A, B, C}
输出：A
步骤3：继续处理队列

  • 出队B，打印B。

  • 访问B的子节点D和E，入队。

队列：[C, D, E]
已访问：{A, B, C, D, E}
输出：A B
步骤4：重复直到队列为空

  • 出队C，打印C。

  • 访问C的子节点F，入队。

队列：[D, E, F]
输出：A B C

  • 出队D（无子节点），出队E（无子节点），出队F（无子节点）。

最终输出：A B C D E F

八 图

一、图的定义

图（Graph） 是一种由 节点（Vertex） 和 边（Edge） 组成的非线性数据结构，用于表示对象之间的关系。

  • 节点（或顶点）：表示实体（如城市、用户、网页等）。

  • 边：表示节点之间的连接关系（如道路、社交关系、超链接等）。

🌰 类比举例：

  • 社交网络：用户是节点，好友关系是边。

  • 地图导航：城市是节点，公路是边。

  • 网页链接：网页是节点，超链接是边。

二、图的组成与关键术语

1. 图的分类
类型描述
无向图边没有方向，表示双向关系（如微信好友）。
有向图边有方向，表示单向关系（如微博关注）。
加权图边带有权重（如地图中道路的长度或耗时）。
无权图边无权重，仅表示是否存在连接。
2. 核心术语
术语描述
度（Degree）节点连接的边数（有向图中分 入度 和 出度）。
路径（Path）从一个节点到另一节点经过的边序列。
环（Cycle）起点和终点相同的路径。
连通图任意两个节点间都有路径。
子图从原图中选取部分节点和边组成的图。

三、图的存储方式

1. 邻接矩阵（Adjacency Matrix）

  • 定义：用二维数组表示节点之间的连接关系。

  • 示例：节点数为 n，矩阵大小为 n×n，matrix[i][j] = 1 表示节点 i 和 j 相连。

// 邻接矩阵示例（无向图）
int graph[4][4] = {{0, 1, 1, 0},{1, 0, 0, 1},{1, 0, 0, 1},{0, 1, 1, 0}
};

  • 特点：

    • 适合稠密图（边多）。

    • 查询快（O(1)），但空间占用高（O(n²)）。

2. 邻接表（Adjacency List）

  • 定义：用链表或数组的数组存储每个节点的邻接节点。

  • 示例：节点 0 的邻居是 1 和 2，节点 1 的邻居是 0 和 3。

// 邻接表示例（C语言）
typedef struct Node {int vertex;struct Node* next;
} Node;Node* graph[4] = {NULL, NULL, NULL, NULL
};// 添加边（无向图）
void addEdge(int src, int dest) {Node* newNode = (Node*)malloc(sizeof(Node));newNode->vertex = dest;newNode->next = graph[src];graph[src] = newNode;// 无向图需双向添加newNode = (Node*)malloc(sizeof(Node));newNode->vertex = src;newNode->next = graph[dest];graph[dest] = newNode;
}

  • 特点：

    • 适合稀疏图（边少）。

    • 空间占用低（O(n + e)），查询邻居需遍历链表（O(degree)）。

四、图的遍历算法

1. 深度优先搜索（DFS, Depth-First Search）

  • 核心思想：沿一条路径深入到底，再回溯探索其他分支。

  • 应用场景：路径查找、拓扑排序、检测环。

// DFS递归实现
void DFS(int v, bool visited[], Node* graph[]) {visited[v] = true;printf("%d ", v);Node* adjNode = graph[v];while (adjNode != NULL) {int neighbor = adjNode->vertex;if (!visited[neighbor]) {DFS(neighbor, visited, graph);}adjNode = adjNode->next;}
}
2. 广度优先搜索（BFS, Breadth-First Search）

  • 核心思想：逐层遍历，先访问离起点最近的节点。

  • 应用场景：最短路径（无权图）、社交网络中的层级关系。

// BFS队列实现
void BFS(int start, Node* graph[], int n) {bool visited[n];for (int i = 0; i < n; i++) visited[i] = false;Queue* q = createQueue();enqueue(q, start);visited[start] = true;while (!isEmpty(q)) {int v = dequeue(q);printf("%d ", v);Node* adjNode = graph[v];while (adjNode != NULL) {int neighbor = adjNode->vertex;if (!visited[neighbor]) {visited[neighbor] = true;enqueue(q, neighbor);}adjNode = adjNode->next;}}
}

五、图的应用场景

领域具体应用
社交网络用户关系分析、推荐系统（如共同好友）。
交通导航最短路径算法（Dijkstra、Floyd-Warshall）。
网络爬虫网页链接分析（PageRank算法）。
电路设计电路节点连接检测、电流路径规划。
生物信息学蛋白质相互作用网络、基因调控网络。

六、代码实战：图的完整实现（邻接表）

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>// 定义邻接表节点
typedef struct Node {int vertex;struct Node* next;
} Node;// 创建图（邻接表）
Node** createGraph(int vertices) {Node** graph = (Node**)malloc(vertices * sizeof(Node*));for (int i = 0; i < vertices; i++) {graph[i] = NULL;}return graph;
}// 添加边（无向图）
void addEdge(Node** graph, int src, int dest) {// 添加src→dest的边Node* newNode = (Node*)malloc(sizeof(Node));newNode->vertex = dest;newNode->next = graph[src];graph[src] = newNode;// 添加dest→src的边（无向图）newNode = (Node*)malloc(sizeof(Node));newNode->vertex = src;newNode->next = graph[dest];graph[dest] = newNode;
}// 打印图
void printGraph(Node** graph, int vertices) {for (int i = 0; i < vertices; i++) {Node* temp = graph[i];printf("节点 %d 的邻居：", i);while (temp) {printf("%d ", temp->vertex);temp = temp->next;}printf("\n");}
}int main() {int vertices = 4;Node** graph = createGraph(vertices);addEdge(graph, 0, 1);addEdge(graph, 0, 2);addEdge(graph, 1, 3);addEdge(graph, 2, 3);printGraph(graph, vertices);return 0;
}

输出：

节点 0 的邻居：2 1 
节点 1 的邻居：3 0 
节点 2 的邻居：3 0 
节点 3 的邻居：2 1

七、总结

图是描述复杂关系的核心数据结构，广泛应用于现实场景。

  • 学习重点：掌握图的存储方式（邻接矩阵 vs 邻接表）、遍历算法（DFS/BFS）、经典问题（最短路径、最小生成树）。

  • 进阶方向：学习 Dijkstra、Prim、Kruskal 等算法，探索图数据库（如 Neo4j）。

如果有具体问题（如“如何实现最短路径算法”），欢迎继续提问！ 🚀

九 总结

排序算法平均 $T(n)$最坏 $T(n)$最好 $T(n)$空间复杂度稳定性
选择排序$O(n^2)$$O(n^2)$$O(n^2)$$O(1)$不稳定
插入排序$O(n^2)$$O(n^2)$$O(n)$$O(1)$稳定
希尔排序$O(n^{1.3})$$O(n^2)$$O(n)$$O(1)$不稳定
冒泡排序$O(n^2)$$O(n^2)$$O(n)$$O(1)$稳定
快速排序$O(n\log_2n)$$O(n^2)$$O(n\log_2n)$$O(n\log_2n)$不稳定

在此理清以下代码思路，我认为还是先理解逻辑结构，在动手去写代码会更好些，本章代码实在是多，我暂时无法理解，希望之后的时间会经常来看看。

相关文章：

  • 【Docker】Docker安装Redis
  • Git命令总结
  • 2025年大厂C++面试题总结与解析
  • 【C++】解析C++面向对象三要素：封装、继承与多态实现机制
  • Remote Desktop安卓远程无法使用中文输入法
  • deepseek讲解如何快速解决内存泄露，内存溢出问题
  • C#数据类型
  • Python中常用的数据类型
  • 反向传播
  • 2、ubantu系统配置OpenSSH | 使用vscode或pycharm远程连接
  • 软件设计师考试《综合知识》CPU考点分析（2019-2023年）——求三连
  • 【QT 项目部署指南】使用 Inno Setup 打包 QT 程序为安装包（超详细图文教程）
  • 基于EFISH-SCB-RK3576/SAIL-RK3576的消防机器人控制器技术方案‌
  • Linux云计算训练营笔记day09（MySQL数据库）
  • 进度管理高分论文
  • 在 Hugo 博客中集成评论系统 Waline 与 浏览量统计
  • 基于“物理—事理—人理”的多源异构大数据融合探究
  • bfs搜索加标记连通区域id实现时间优化（空间换时间）
  • Go语言八股之Mysql事务
  • 扬州卓韵酒店用品：优质洗浴用品，提升酒店满意度与品牌形象
  • 降水较常年同期少五成，安徽四大水利工程调水超11亿方应对旱情
  • 端午小长假前夜火车票今日开抢，多个技巧提高购票成功率
  • 上海“城市文明开放麦”全城总动员，樊振东担任首位上海城市文明大使
  • 金正恩观摩朝鲜人民军各兵种战术综合训练
  • 西北大学副校长成陕西首富？旗下巨子生物去年净利超20亿，到底持股多少
  • A股三大股指涨跌互现：银行股领涨，两市成交12915亿元