【漫话机器学习系列】258.拐点（Inflection Point）

拐点（Inflection Point）详解：定义、原理与应用

在数学分析与数据建模中，“拐点（Inflection Point）”是一个非常重要的概念。今天这篇文章，我们将结合图示，深入理解拐点的定义、数学意义、识别方法以及实际应用场景。

---

什么是拐点？

拐点，英文称为 Inflection Point，是曲线形状发生变化的特殊位置。

正式定义：

拐点是函数图像上由凸函数变成凹函数的点，或者是由凹函数变成凸函数的点。

简单来说，就是函数的曲率方向发生改变的位置。在拐点处，曲线从“向上弯”变为“向下弯”，或者反之。

图示说明：
下图直观展示了拐点的位置：

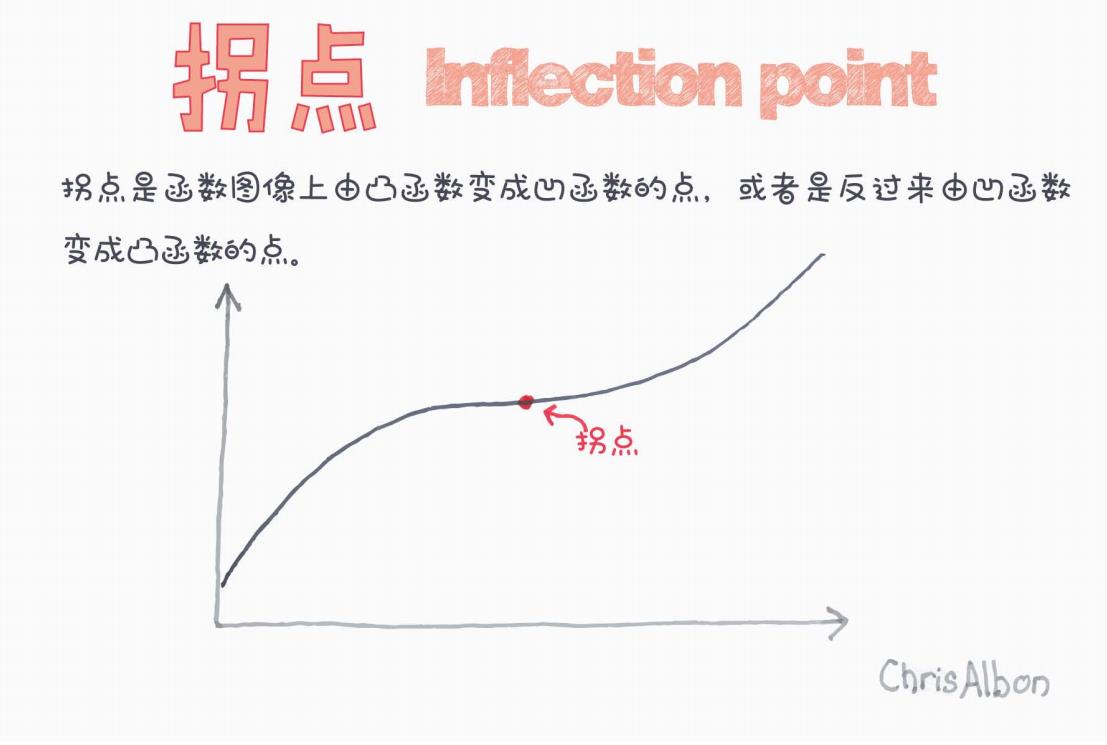
在图中，可以看到曲线在红色标记点（拐点）处，发生了由凹变凸的转变。

---

数学角度理解拐点

1. 凸性与凹性

在拐点讨论中，凸性（convexity）和凹性（concavity）是基础。

• 如果函数在某区间上开口朝上（像一个笑脸弧线），则称为凸。

• 如果函数在某区间上开口朝下（像一个皱眉的弧线），则称为凹。

2. 二阶导数与拐点

二阶导数 f''(x) 提供了判断函数曲率的依据：

• 当 f''(x) > 0 时，函数是凸的。

• 当 f''(x) < 0 时，函数是凹的。

• 当 f''(x) = 0 并且符号发生变化时，x 对应的位置就是拐点。

拐点判定步骤：

1. 计算函数的二阶导数 f''(x)。

2. 解方程 f''(x) = 0，找出候选点。

3. 检查这些点在前后左右的二阶导数符号是否发生变化。

4. 符号变化的点即为拐点。

---

拐点在实际中的应用

拐点不仅是数学分析中的基础概念，还在各种实际应用中扮演重要角色，比如：

1. 机器学习与深度学习

在训练过程中，学习曲线的拐点可能意味着模型开始过拟合，需要采取正则化或早停等措施。

2. 数据分析与趋势预测

在销售增长曲线中，拐点可能代表市场饱和点或者增长加速点，有助于企业做出战略调整。

3. 金融投资

股价曲线的拐点常被用于判断趋势反转，是技术分析中的关键节点。

4. 生物统计与医学研究

疾病传播曲线的拐点可以用来预测疫情爆发、拐点控制等。

---

举例：拐点计算示范

以简单函数 为例：

1. 一阶导数：

2. 二阶导数：

令二阶导数为零：

检查 x=0 左右的二阶导数符号变化：

• 当 x < 0，f''(x) < 0（凹）

• 当 x > 0，f''(x) > 0（凸）

所以，x=0 是函数 的拐点。

---

小结

• 拐点是曲线由凸变凹或由凹变凸的位置。

• 二阶导数为判断拐点提供了有效的工具。

• 拐点分析在机器学习、金融、疫情分析等领域都有重要应用。

掌握拐点的概念不仅能提升数学素养，也能帮助我们更好地理解和应用数据变化背后的规律。

---

作者注：本文参考了 Chris Albon 的手绘图进行解释，图片风格清新有趣，希望能帮助大家更轻松地理解这一抽象概念。

---

如果你喜欢这样的图文结合讲解，欢迎点赞、收藏、关注我！