多令牌预测Multi-Token Prediction(MTP)
多令牌预测(MTP)
- 多令牌预测(MTP)
- 1.概念
- 2、原理
- 2.1BPD
- 2.2Meta改进版
- 单次训练(示意图)
- batch批量训练(示意图)
- 2.3DeepSeek改进版MTP
- 原理
- Teacher forcing和free-running模式
- 训练的输入系列预测对应位置
- 单次训练(示意图)
- batch批量训练(示意图)
- 推理
- 2.4 对比(训练推理)
- 3、DeepSeek MTP实例说明
- 一、核心设计逻辑:从单令牌到多令牌预测
- 二、MTP模块实现:以D=2为例(预测未来2个令牌)
- 1. **k=1深度:预测第i+1个令牌(下一个令牌)**
- 2. **k=2深度:预测第i+2个令牌(下下个令牌)**
- 3. **因果链保持**:
- 三、训练目标:多深度损失计算实例
- 四、推理阶段:推测解码加速实例
- 五、关键优势与对比
- 总结:MTP如何提升模型性能?
- 4、Multi-Token Prediction(原文解释)
- MTP模块
- MTP训练目标
- MTP在推理中的应用
本文参考自论文:DeepSeek-V3论文笔记
多令牌预测(MTP)
1.概念
什么是MTP(what)
MTP(Multi-Token Prediction)实际上就是将大模型原始的1-token的生成,转变成multi-token的生成,从而提升训练和推理的性能。具体来说,在训练阶段,一次生成多个后续token,可以一次学习多个后续位置上的label,进而有效提升样本的利用效率,提升训练速度;在推理阶段通过一次生成多个后续token,实现成倍的推理加速来提升推理性能。
当前主流的大模型(LLMs)都是decoder-base的模型结构,也就是无论在模型训练还是在推理阶段,对于一个序列的生成过程,都是token-by-token的。每次在生成一个token的时候,都要频繁跟访存交互,加载KV-Cache,再通过多层网络做完整的前向计算。对于这样的访存密集型的任务,通常会因为访存效率形成训练或推理的瓶颈。针对token-by-token生成效率的瓶颈,业界很多方法来优化,包括减少存储的空间和减少访存次数等,进而提升训练和推理性能。
2、原理
2.1BPD
Blockwise Parallel Decoding
首先我们来看一篇Google的工作,这是Google在18年发表在NIPS上的工作(18年是Transformer诞生的元年)。
paper:Blockwise Parallel Decoding for Deep Autoregressive Models





Blockwise Parallel Decoding 的核心内容,该方法主要是为了做推理阶段的并行加速而设计的。虽然命名上没有遵循MPT类,但后面一些演进的方法比如Speculative Sample和下面要介绍的Meta’s MTP等,都有该方法设计的影子。
参考:https://zhuanlan.zhihu.com/p/18056041194
2.2Meta改进版
原始版MTP有个什么问题呢?因为那时候当前LLM的decoder架构还不受到重视,因此meta结合当前LLM的架构,重新设计了更符合大模型的MTP。
这是meta 于2024年4月发表的一篇工作。
paper : Better & Faster Large Language Models via Multi-token Prediction




单次训练(示意图)




batch批量训练(示意图)
Meta GPU批次并行预测(batch)
因为GPU在训练时,是支持批量同时训练的,多条数据组成一个batch批次,同时并行计算,因此,可以把上面几个训练画在一张图里,就变成了如下原始论文形式:

2.3DeepSeek改进版MTP
原理
DeepSeek-V3/R1与Meta的多令牌预测存在两个关键差异:“与Gloeckle等人(2024)[Meta Research]不同,他们使用独立的输出头并行预测D个额外的令牌,而我们则按顺序预测额外的令牌,并在每个预测深度保持完整的因果链。”——DeepSeek-V3
Meta的模型预测4个令牌,而DeepSeek-V3预测2个令牌。Meta模型的预测头相互独立,而DeepSeek-V3的预测头则是顺序连接的。
多 Token 预测(MTP):

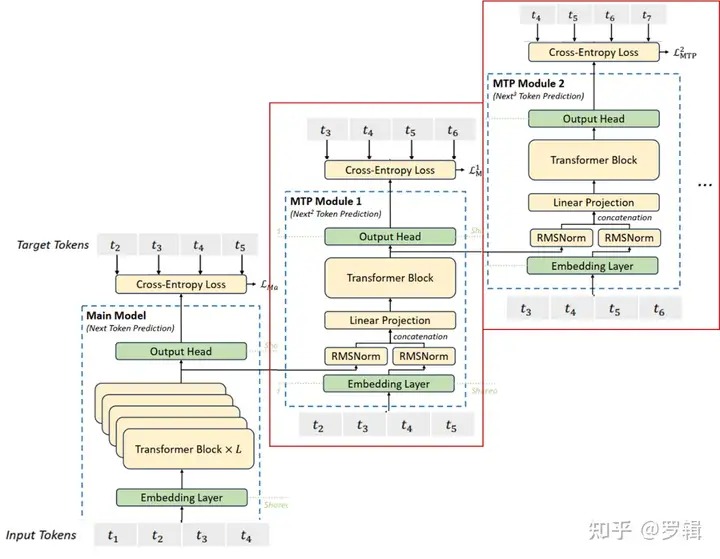
图 3 |我们的多令牌预测 (MTP) 实施图示。我们保留了完整的因果链,用于预测每个深度的每个代币。

MTP在DeepSeek-R1中是如何工作的呢?让我们逐步解析相关图表: 在训练过程中,输入令牌(位于左下角)先经过嵌入层,然后传播通过所有的Transformer块/层。



Teacher forcing和free-running模式


训练的输入系列预测对应位置



单次训练(示意图)

batch批量训练(示意图)
DeepSeek GPU批次并行预测(batch)
参照3.2.1中meta MTP的并行“因果关系”训练的具体过程,可以把一个batch中的多条记录,画在一张图上,就成了如下所示:美化一下,调整一下排版,就成了DeepSeek论文中的样子。
推理


2.4 对比(训练推理)
传统方法的问题(预测下一个token):
- 训练阶段:token-by-token生成,是一种感知局部的训练方法,难以学习长距离的依赖关系。
- 推理阶段:逐个token生成,推理速度较慢
MTP方法(一次预测多个token):
- 训练阶段:通过预测多步token,迫使模型学到更长的token依赖关系,从而更好理解上下文,避免陷入局部决策的学习模式。同时一次预测多个token,可大大提高样本的利用效率,相当于一次预估可生成多个<predict, label>样本,来更新模型,有助于模型加速收敛。
- 推理阶段:并行预估多个token,可提升推理速度
DeepSeek MTP与Meta方案的对比
| 特性 | Meta的MTP | DeepSeek的MTP |
|---|---|---|
| 预测方式 | 并行独立预测多个令牌(4个独立头) | 级联顺序预测(2-3个模块) |
| 因果性 | 可能破坏因果链 | 严格保持因果链 |
| 参数共享 | 独立输出头 | 共享嵌入、输出头和部分Transformer层 |
| 适用场景 | 短文本快速生成 | 长文本连贯性要求高的任务 |
训练推理
| 维度 | 训练阶段(Training) | 推理阶段(Inference) |
|---|---|---|
| 输入数据 | 使用完整的目标序列(真实标签),通过掩码或分组强制模型并行预测多令牌。 | 仅依赖已生成的令牌(初始为<s>),逐步扩展生成序列。 |
| 目标函数 | 计算多令牌的联合概率损失(如交叉熵),优化模型对全局依赖的建模能力。 | 通过解码策略(如波束搜索)生成高概率序列,无需反向传播。 |
| 生成逻辑 | 教师强制(Teacher Forcing):直接输入真实令牌,无需模型自回归生成。 | 自回归或半自回归:依赖前序生成结果,逐步预测后续多令牌。 |
| 并行性 | 高度并行:一次处理多个目标位置的真实令牌,批量计算损失。 | 部分并行:每次生成一批令牌(如k个),但需按步骤迭代生成。 |
参考:
https://zhuanlan.zhihu.com/p/18056041194
https://blog.csdn.net/weixin_43290383/article/details/146245802
https://zhuanlan.zhihu.com/p/24226643215
https://cloud.tencent.com/developer/article/2505000
备份:链接
3、DeepSeek MTP实例说明
DeepSeek-V3的多令牌预测(MTP)通过预测未来多个令牌优化训练,提升模型对序列生成的规划能力。以下结合具体示例,从设计逻辑、实现步骤、训练目标及推理应用展开说明:
一、核心设计逻辑:从单令牌到多令牌预测
传统单令牌预测:
- 输入序列:
[我, 吃, 苹, 果] - 预测目标:每个位置仅预测下一个令牌(如“我”→预测“吃”,“吃”→预测“苹”)。
- 缺点:训练信号稀疏,模型需多次迭代才能学习长距离依赖。
MTP多令牌预测:
- 目标:每个位置预测未来D个令牌(如D=2时,“我”→预测“吃”和“苹”,“吃”→预测“苹”和“果”)。
- 优势:密集训练信号,强制模型提前规划多步生成,提升长序列生成效率。
二、MTP模块实现:以D=2为例(预测未来2个令牌)
假设输入序列为 [t₁=我, t₂=吃, t₃=苹, t₄=果],序列长度T=4,MTP模块按深度k=1和k=2顺序预测:
1. k=1深度:预测第i+1个令牌(下一个令牌)
-
输入处理:
- 对于第i=1个令牌“我”,k=1时,前一层表示h⁰₁为主模型输出的“我”的表示。
- 结合未来第i+1=2个令牌“吃”的嵌入:
h 1 ′ 1 = M 1 [ RMSNorm ( h 1 0 ) ; RMSNorm ( Emb ( t 2 = 吃 ) ) ] h'^1_1 = M_1 \left[ \text{RMSNorm}(h^0_1) ; \text{RMSNorm}(\text{Emb}(t₂=吃)) \right] h1′1=M1[RMSNorm(h10);RMSNorm(Emb(t2=吃))]
(拼接并投影为2d维度,d为隐藏层维度)
-
Transformer处理:
- 将h’^1_1输入TRM₁,生成当前深度表示h¹₁,用于预测第i+1+1=2+1=3个令牌“苹”(实际应为i+k+1=1+1+1=3,即t₃)。
-
输出预测:
- 共享输出头计算概率分布:
P 3 1 = OutHead ( h 1 1 ) (预测t₃=苹的概率) P^1_3 = \text{OutHead}(h^1_1) \quad \text{(预测t₃=苹的概率)} P31=OutHead(h11)(预测t₃=苹的概率)
- 共享输出头计算概率分布:
2. k=2深度:预测第i+2个令牌(下下个令牌)
-
输入处理:
- 对于i=1,k=2时,前一层表示h¹₁(k=1的输出)。
- 结合未来第i+2=3个令牌“苹”的嵌入:
h 1 ′ 2 = M 2 [ RMSNorm ( h 1 1 ) ; RMSNorm ( Emb ( t 3 = 苹 ) ) ] h'^2_1 = M_2 \left[ \text{RMSNorm}(h^1_1) ; \text{RMSNorm}(\text{Emb}(t₃=苹)) \right] h1′2=M2[RMSNorm(h11);RMSNorm(Emb(t3=苹))]
-
Transformer处理:
- 输入TRM₂生成h²₁,用于预测第i+2+1=4个令牌“果”(t₄)。
-
输出预测:
P 4 2 = OutHead ( h 1 2 ) (预测t₄=果的概率) P^2_4 = \text{OutHead}(h^2_1) \quad \text{(预测t₄=果的概率)} P42=OutHead(h12)(预测t₄=果的概率)
3. 因果链保持:
- 预测t₃时,仅依赖t₁和t₂的信息;预测t₄时,依赖t₁、t₂、t₃的信息,确保每个预测步骤符合因果关系(即不依赖未来未生成的令牌)。
三、训练目标:多深度损失计算实例
假设T=4,D=2,λ=0.3,计算MTP损失:
- k=1深度损失:
- 预测范围:i=2+1=3到T+1=5(实际序列长度为4,故有效范围i=3到4)。
- 真实令牌:t₃=苹,t₄=果。
- 损失:
L 1 MTP = − 1 4 ( log P 3 1 [ 苹 ] + log P 4 1 [ 果 ] ) \mathcal{L}^{\text{MTP}}_1 = -\frac{1}{4} \left( \log P^1_3[苹] + \log P^1_4[果] \right) L1MTP=−41(logP31[苹]+logP41[果])
- k=2深度损失:
- 预测范围:i=2+2=4到T+1=5(仅i=4)。
- 真实令牌:t₄=果。
- 损失:
L 2 MTP = − 1 4 log P 4 2 [ 果 ] \mathcal{L}^{\text{MTP}}_2 = -\frac{1}{4} \log P^2_4[果] L2MTP=−41logP42[果]
- 整体MTP损失:
L MTP = 0.3 × 1 2 ( L 1 MTP + L 2 MTP ) \mathcal{L}^{\text{MTP}} = 0.3 \times \frac{1}{2} \left( \mathcal{L}^{\text{MTP}}_1 + \mathcal{L}^{\text{MTP}}_2 \right) LMTP=0.3×21(L1MTP+L2MTP)
该损失与主模型的单令牌预测损失共同优化模型,强化多步生成能力。
四、推理阶段:推测解码加速实例
- 传统解码:逐令牌生成,生成“我吃苹果”需4次迭代(每次生成1个令牌)。
- MTP推测解码:
- 通过MTP模块提前预测下2个令牌候选(如“吃”“苹”)。
- 验证候选令牌正确性,若正确则一次性生成,减少迭代次数(如2次迭代生成4个令牌)。
- 效果:解码速度提升1.8倍,尤其适合长文本生成(如代码、数学证明)。
五、关键优势与对比
| 特性 | DeepSeek-V3 MTP | Gloeckle et al. (2024) |
|---|---|---|
| 预测方式 | 顺序预测(保持因果链) | 并行独立预测(多输出头) |
| 参数共享 | 共享主模型嵌入层和输出头 | 独立输出头(参数更多) |
| 核心目标 | 训练阶段增强模型能力 | 推理阶段加速(推测解码) |
| 典型应用 | 提升数学、代码长序列生成质量 | 单纯加速生成速度 |
总结:MTP如何提升模型性能?
通过顺序预测未来多个令牌,MTP在训练阶段为模型提供更密集的监督信号,迫使模型学习序列生成的长期依赖(如语法、逻辑连贯)。例如,生成数学证明时,预测下一步公式推导步骤;生成代码时,提前规划函数调用顺序。这种预规划能力在推理阶段通过推测解码进一步加速,实现“训练提效+推理加速”的双重优势,是DeepSeek-V3在复杂任务上表现突出的关键技术之一。
4、Multi-Token Prediction(原文解释)
受格洛克勒(Gloeckle)等人(2024年)启发,我们为DeepSeek-V3设计了**多令牌预测(Multi-Token Prediction, MTP)**目标,将每个位置的预测范围扩展到多个未来令牌。一方面,MTP目标通过密集化训练信号提升数据效率;另一方面,它使模型能够预规划表示,从而更好地预测未来令牌。图3展示了我们的MTP实现方式。不同于格洛克勒等人(2024年)使用独立输出头并行预测D个额外令牌的方法,我们采用顺序预测额外令牌的方式,并在每个预测深度保持完整的因果链。本节将详细介绍MTP的实现细节。
MTP模块
具体而言,我们的MTP实现通过D个顺序模块预测D个额外令牌。第k个MTP模块包含一个共享嵌入层Emb(·)、一个共享输出头OutHead(·)、一个Transformer块TRMₖ(·)和一个投影矩阵𝑀ₖ∈Rᵈײᵈ。对于第i个输入令牌𝑡ᵢ,在第k个预测深度,我们首先将第(i)个令牌在(k−1)深度的表示h⁽ᵏ⁻¹⁾ᵢ∈Rᵈ与第(i+k)个令牌的嵌入Emb(𝑡ᵢ₊ₖ)∈Rᵈ通过线性投影结合:
h i ( k ) = 𝑀 k [ RMSNorm ( h i ( k − 1 ) ) ; RMSNorm ( Emb ( 𝑡 i + k ) ) ] ( 21 ) h'⁽ᵏ⁾ᵢ = 𝑀ₖ \left[ \text{RMSNorm}(h⁽ᵏ⁻¹⁾ᵢ) ; \text{RMSNorm}(\text{Emb}(𝑡ᵢ₊ₖ)) \right] \quad (21) hi(k)=Mk[RMSNorm(hi(k−1));RMSNorm(Emb(ti+k))](21)
其中[·; ·]表示拼接操作。特别地,当k=1时,h⁽ᵏ⁻¹⁾ᵢ为主模型输出的令牌表示。注意,每个MTP模块的嵌入层与主模型共享。拼接后的h’⁽ᵏ⁾ᵢ作为第k深度Transformer块的输入,生成当前深度的输出表示h⁽ᵏ⁾ᵢ:
h 1 : 𝑇 − k ( k ) = TRMₖ ( h 1 : 𝑇 − k ( k ) ) ( 22 ) h⁽ᵏ⁾_{1:𝑇−ᵏ} = \text{TRMₖ}(h'⁽ᵏ⁾_{1:𝑇−ᵏ}) \quad (22) h1:T−k(k)=TRMₖ(h1:T−k(k))(22)
其中T为输入序列长度,i:j表示包含左右边界的切片操作。最后,共享输出头以h⁽ᵏ⁾ᵢ为输入,计算第k个额外预测令牌的概率分布𝑃⁽ᵏ⁾_{𝑖+𝑘+1}∈Rᵛ(V为词汇表大小):
𝑃 𝑖 + 𝑘 + 1 ( k ) = OutHead ( h i ( k ) ) ( 23 ) 𝑃⁽ᵏ⁾_{𝑖+𝑘+1} = \text{OutHead}(h⁽ᵏ⁾ᵢ) \quad (23) Pi+k+1(k)=OutHead(hi(k))(23)
输出头OutHead(·)将表示线性映射为对数概率(logits),并通过Softmax函数计算第k个额外令牌的预测概率。每个MTP模块的输出头同样与主模型共享。我们保持预测因果链的原则与EAGLE(Li等人,2024b)类似,但其主要目标是推测解码(Leviathan等人,2023;Xia等人,2023),而我们利用MTP优化训练过程。
MTP训练目标
对于每个预测深度,计算交叉熵损失𝐿⁽ᵏ⁾_MTP:
𝐿 MTP ( k ) = CrossEntropy ( 𝑃 2 + 𝑘 : 𝑇 + 1 ( k ) , 𝑡 2 + 𝑘 : 𝑇 + 1 ) = − 1 𝑇 ∑ 𝑖 = 2 + 𝑘 𝑇 + 1 log 𝑃 𝑖 ( k ) [ 𝑡 i ] ( 24 ) 𝐿⁽ᵏ⁾_{\text{MTP}} = \text{CrossEntropy}(𝑃⁽ᵏ⁾_{2+𝑘:𝑇+1}, 𝑡_{2+𝑘:𝑇+1}) = -\frac{1}{𝑇} \sum_{𝑖=2+𝑘}^{𝑇+1} \log 𝑃⁽ᵏ⁾_𝑖[𝑡ᵢ] \quad (24) LMTP(k)=CrossEntropy(P2+k:T+1(k),t2+k:T+1)=−T1i=2+k∑T+1logPi(k)[ti](24)
其中T为序列长度,𝑡ᵢ为第i位置的真实令牌,𝑃⁽ᵏ⁾_𝑖[𝑡ᵢ]为第k个MTP模块对𝑡ᵢ的预测概率。最终,将所有深度的MTP损失取平均并乘以权重因子λ,得到整体MTP损失𝐿_MTP,作为DeepSeek-V3的额外训练目标:
𝐿 MTP = λ 𝐷 ∑ 𝑘 = 1 𝐷 𝐿 MTP ( k ) ( 25 ) 𝐿_{\text{MTP}} = \frac{\lambda}{𝐷} \sum_{𝑘=1}^{𝐷} 𝐿⁽ᵏ⁾_{\text{MTP}} \quad (25) LMTP=Dλk=1∑DLMTP(k)(25)
MTP在推理中的应用
MTP策略主要用于提升主模型性能,因此推理时可直接丢弃MTP模块,主模型独立正常运行。此外,我们还可将MTP模块用于推测解码,进一步降低生成延迟。
