激活函数(sigmoid、Tanh、ReLu、softmax、softmin、LogSoftma)公式,作用,使用场景和python代码(包含示例)详解
目录
- 1. Sigmoid
- 2. Tanh(双曲正切)
- 3. ReLU(Rectified Linear Unit)
- 4. Softmax
- 5. Softmin
- 6. Log Softmax
激活函数是一些非线性、可微分的函数。在神经网络中使用激活函数可为网络加入非线性特性。

1. Sigmoid
- 公式
f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1
-
作用
-
将任意实数映射到 (0,1) 区间内
-
具有平滑、可导的特性
-

-
优点:
- Sigmoid函数的输出范围是0到1,输出范围固定。
- 可解释为概率,适合作为模型的输出函数用于输出0~1范围内的概率值;平滑且易于微分。比如二分类任务。
-
缺点:
- 容易出现梯度消失(当 ∣ x ∣ |x| ∣x∣ 很大或很小时,梯度趋近于 0),导致模型训练困难
- 输出非 0 均值,可能导致后续层学习效率降低。
- 而且,它的输出不是以 0 为中心的,可能会影响模型的收敛速度。
-
使用场景
-
二分类模型输出层(与交叉熵损失配合)
-
早期浅层神经网络中间层(现多用 ReLU 代替)
-
Python 实现
import numpy as npdef sigmoid(x):return 1 / (1 + np.exp(-x))# 示例
x = np.linspace(-10,10,1000) # 生成1000个点,从-10到10
y = sigmoid(x)
2. Tanh(双曲正切)
- 公式
tanh ( x ) = e x − e − x e x + e − x \tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} tanh(x)=ex+e−xex−e−x
-
作用
-
将实数映射到 (−1,1) 区间
-
输出均值接近 0,有助于缓解梯度下降时的“偏移”问题
-

-
优点
- 输出以 0 为中心(输出均值为 0)
- 相比于 Sigmoid 函数输出范围在(0, 1),tanh函数的输出范围是(-1, 1),这使得它的输出值有正有负,在一定程度上可以加快模型的收敛速度,相比 Sigmoid 更快收敛。
-
缺点
- 梯度消失问题:当输入值 ∣ x ∣ |x| ∣x∣非常大或者非常小时,tanh函数的导数接近于 0,这会导致在反向传播过程中梯度变得非常小,从而使得模型的训练变得困难,甚至无法收敛。
- 计算复杂度较高:tanh函数涉及到指数运算,相比于一些简单的激活函数(如 ReLU),计算复杂度较高。
-
使用场景
-
循环神经网络(RNN)隐藏层
-
需要零均值输出的网络层
-
Python 实现
def tanh(x):return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))# 示例
x = np.linspace(-10,10,1000)
y = tanh(x)
3. ReLU(Rectified Linear Unit)
- 公式
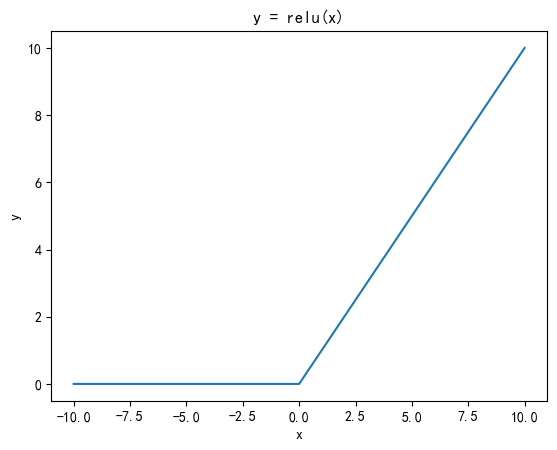
R e L U ( x ) = max ( 0 , x ) \mathrm{ReLU}(x) = \max(0, x) ReLU(x)=max(0,x)
即输入值大于 0 时输出该值;输入值小于等于 0 时,输出 0。
-
作用
-
对输入进行简单截断,将负值置为 0,正值保持不变
-
保持稀疏激活,有助于缓解梯度消失问题
-
-
优点
- 解决了梯度消失问题,当输入值为正时,神经元不会饱和,能够减轻梯度消失
- 计算复杂度低,不需要进行指数运算,收敛快
-
缺点
- 与sigmoid一样,其输出不是以0为中心的
- 当输出为负时,梯度为0。这个神经元及之后的神经元梯度永远为0,不再对任何数据有所响应,导致相应参数永远不会被更新。负值部分恒为 0,可能导致“神经元死亡”(dead ReLU)
-
使用场景
- 几乎所有现代深度神经网络的隐藏层(如卷积网络、全连接网络)
Python 实现
def relu(x):return np.maximum(0, x)# 示例
x = np.linspace(-10,10,1000)
y = relu(x)
4. Softmax
- 公式
对于输入向量 x = [ x 1 , x 2 , . . . , x n ] , \mathbf{x} = [x_1, x_2, ..., x_n], x=[x1,x2,...,xn],
s o f t m a x ( x i ) = e x i ∑ j = 1 n e x j \mathrm{softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}} softmax(xi)=∑j=1nexjexi

如果有 n n n个元素,则首先求 e x p ( x 1 ) exp^{(x_1)} exp(x1)到 e x p ( x n ) exp^{(x_n)} exp(xn)的和,任意 e x p ( x i ) exp^{(x_i)} exp(xi)除以这个和,得到的结果都在0到1之间,且 S o f t m a x ( x 1 ) Softmax(x_1) Softmax(x1)到 S o f t m a x ( x n ) Softmax(x_n) Softmax(xn)的和为1。
-
作用
- 将向量映射为概率分布(所有输出和为 1,且均为正数)
-
优点
- 输出概率分布:Softmax 函数将原始的得分转换为概率分布,使得模型的输出具有明确的概率意义,方便进行多分类决策。
- 可微性:Softmax 函数是可微的,这使得它可以用于基于梯度的优化算法,如随机梯度下降(SGD),来训练模型。
-
缺点
- 计算复杂度高:由于涉及指数运算,Softmax 函数的计算复杂度较高,尤其是当输入向量的维度较大时,会增加计算时间和内存开销。
- 对异常值敏感:指数函数会放大输入值之间的差异,因此 Softmax 函数对异常值比较敏感。如果输入向量中存在一个较大的值,那么对应的输出概率会趋近于 1,而其他值对应的概率会趋近于 0。
-
使用场景
- 多分类模型的输出层(通常配合交叉熵损失使用)
Python 实现
def Softmax(x):ex = np.exp(x - np.max(x)) # 减去最大值,数值稳定return ex / np.sum(ex)# 示例
x = np.linspace(-10,10,1000)
y = Softmax(x)
5. Softmin
- 公式
s o f t m i n ( x i ) = e − x i ∑ j = 1 n e − x j \mathrm{softmin}(x_i) = \frac{e^{-x_i}}{\sum_{j=1}^n e^{-x_j}} softmin(xi)=∑j=1ne−xje−xi

相当于对 x \mathbf{x} x 取负后再做 softmax。Softmin 激活函数是 Softmax 激活函数的一种变体,它同样将一组实数转换为概率分布,不过更倾向于突出较小的值。
-
作用
- 将向量映射为“反向”概率分布:较小的输入对应较大的概率
-
优点
- 概率解释:和 Softmax 函数一样,Softmin 函数的输出可以被解释为概率分布,这使得它在需要进行概率建模和分类决策的任务中非常有用。
- 可微性:Softmin 函数是可微的,这意味着它可以用于基于梯度的优化算法,例如在训练神经网络时使用的**随机梯度下降(SGD)**及其变种算法。
-
缺点
- 计算复杂度:和 Softmax 函数类似,由于涉及指数运算,Softmin 函数的计算复杂度较高,尤其是在处理高维向量时,会消耗较多的计算资源和时间。
- 对异常值敏感:指数运算会放大输入值之间的差异,所以 Softmin 函数对输入向量中的异常值比较敏感。一个较大的输入值经过取负和指数运算后会使对应的输出概率趋近于 0,而其他值对应的概率会相对增大。
-
使用场景
- 需要强调低分值项概率的场景(较少见)
Python 实现
def Softmin(x):ex = np.exp(-(x - np.min(x))) # 可减去最小值确保稳定return ex / np.sum(ex)# 示例
x = np.linspace(-10,10,1000)
y = Softmin(x)
6. Log Softmax
- 公式
L o g S o f t m a x ( x i ) = log ( s o f t m a x ( x i ) ) = l o g ( e x i ∑ j = 1 n e x j ) \mathrm{Log\ Softmax}(x_i) = \log\bigl(\mathrm{softmax}(x_i)\bigr) = log(\frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}}) Log Softmax(xi)=log(softmax(xi))=log(∑j=1nexjexi)

LogSoftmax 激活函数是对 Softmax 函数的输出取自然对数。
-
作用
-
直接得到对数概率,数值更稳定、避免 underflow
-
与负对数似然损失(NLLLoss)结合时,效率更高
-
-
优点
- Log Softmax 在一定程度上缓解了 Softmax 函数对异常值敏感的问题。
-
缺点
- 理解难度稍高:相较于 Softmax 函数,Log Softmax 函数的输出是对数概率,不像 Softmax 函数的输出那样直观地表示概率,理解起来需要一定的数学基础。
- 计算复杂度相对较高:虽然 Log Softmax 函数能解决数值稳定性问题,但它在计算过程中多了对数运算,相较于直接使用 Softmax 函数,计算复杂度会有所增加。
-
使用场景
-
PyTorch 等框架中,多分类任务常将最后一层与
nn.LogSoftmax+nn.NLLLoss配合 -
需要直接使用对数概率进行后续计算的场景
-
Python 实现
def Softmax(x):ex = np.exp(x - np.max(x)) # 减去最大值,数值稳定return ex / np.sum(ex)def Log_Softmax(x):return np.log(Softmax(x))# 示例
x = np.linspace(-10,10,1000)
y = Log_Softmax(x)
小结与示例对比
import numpy as npx = np.array([-2.0, 0.0, 2.0])print("Sigmoid:", sigmoid(x))
print("Tanh :", tanh(x))
print("ReLU :", relu(x))
print("Softmax:", softmax(x))
print("Softmin:", softmin(x))
print("LogSoftmax:", log_softmax(x))
运行结果示例(约):
| 函数 | -2.0 | 0.0 | 2.0 |
|---|---|---|---|
| Sigmoid | 0.1192 | 0.5000 | 0.8808 |
| Tanh | -0.964 | 0.0000 | 0.9640 |
| ReLU | 0.0000 | 0.0000 | 2.0000 |
| Softmax | 0.0158 | 0.1173 | 0.8668 |
| Softmin | 0.8668 | 0.1173 | 0.0158 |
| Log Softmax | -4.1429 | -2.142 | -0.1429 |
