基于扩展卡尔曼滤波（EKF）目标轨迹算法仿真实例

摘要：本博文主要介绍扩展卡尔曼滤波算法在目标轨迹跟踪中的应用。首先简单介绍了EKF算法的原理，随后通过具体的雷达仿真案例加深各位伙伴对EKF滤波算法的理解。

1.简介

        在动态系统的状态估计领域，实时、精准地追踪目标的位置、速度等状态量是自动驾驶、机器人导航、航空航天等应用的核心需求。1960年，卡尔曼滤波（Kalman Filter, KF）的提出为线性系统提供了最优估计的理论框架，其通过递归融合模型预测与传感器观测，在高斯噪声假设下实现了高效的状态更新。然而，现实世界的物理系统往往呈现出复杂的非线性特性——无论是无人机的姿态动力学、移动机器人的运动模型，还是卫星轨道的引力摄动，其状态转移或观测过程均难以用线性方程精确描述。这种非线性与噪声的耦合，使得经典卡尔曼滤波在直接应用时面临根本性局限：线性假设的崩塌将导致估计误差迅速累积甚至发散。

        为解决这一挑战，扩展卡尔曼滤波（Extended Kalman Filter, EKF）应运而生。20世纪70年代，研究者们提出通过对非线性系统进行局部线性化，将卡尔曼滤波的递推框架扩展至弱非线性场景。EKF的核心思想在于：在当前状态估计点处，利用一阶泰勒展开对非线性函数进行近似，从而将非线性问题转化为局部线性问题，并沿用卡尔曼滤波的预测-更新流程。这一方法不仅继承了KF的计算高效性，还显著拓宽了其应用边界，成为早期非线性估计的主流工具。例如，在阿波罗登月计划中，EKF被用于处理航天器导航中的非线性轨道动力学；在现代自动驾驶中，它助力车辆融合多传感器数据，实现复杂路况下的精准定位。

        然而，EKF并非“万能钥匙”。其一阶近似的本质使其对强非线性系统（如高速旋转或剧烈机动）的适应性受限，线性化误差可能导致估计偏差甚至滤波发散。尽管如此，EKF凭借其简洁的数学形式、较低的计算开销，以及易于工程实现的特性，至今仍在机器人SLAM（同步定位与建图）、惯性导航、目标跟踪等领域占据重要地位。它不仅是理解非线性滤波理论的基石，更在工程实践中架起了从理想线性模型到真实非线性世界的桥梁，为后续无迹卡尔曼滤波（UKF）、粒子滤波（PF）等更复杂方法的发展奠定了基础。理解EKF的诞生背景与设计哲学，不仅是掌握现代状态估计技术的起点，也是优化实际系统中滤波性能的关键一步。

2.EKF算法原理

        在讲解EKF算法的原理之前，首先让我们简单的回顾一下卡尔曼滤波的思想。卡尔曼滤波是一种针对线性高斯系统的最优状态估计算法，通过递归方式融合系统模型和传感器观测数据，实现对动态系统状态的实时估计。其核心步骤分为：（1）预测(基于系统模型预测下一时刻状态)；（2）更新（利用观测数据修正预测值）。实际应用中，要想达到预期的性能效果，KF就要要求系统满足线性（状态转移和观测矩阵为线性）和高斯噪声假设，而实际系统（如机器人运动、目标跟踪）多为非线性。

        为了弥补KF方法的不足，EKF通过局部线性化解决非线性系统的状态估计问题，具体方法：(1)对非线性模型进行一阶泰勒展开，在估计点附近线性化。(2)使用线性化后的近似模型，沿用KF的框架进行递推。说白了EKF就是对一些非线性运动的目标，通过泰勒展开的方法使其在局部线性化，随后采用KF方法进行预测和修正。假设系统状态方程为：

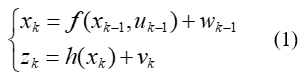
式中表示状态向量（如距离、速度等），表示输入控制，表示观测向量。表示过程噪声，表示观测噪声。和分别表示非线性状态转移方程和观测方程。对非线性函数在当前估计点进行一阶泰勒展开，分别状态转移雅可比矩阵和观测雅可比矩阵，结合这两个雅可比矩阵可得到近似的线性化模型如下：

其中表示输入控制矩阵，例如目标运动的加速度等。和分别由下式求得： 

 

3.EKF算法流程

Step1：初始化

1. 状态估计。
2. 误差协方差矩阵。

Step2: 预测

1. 状态一步预测

     2.误差协方差预测

Step3: 预测

1. 计算卡尔曼增益

     2.状态更新

    3.协方差矩阵更新

在此值得说明的是，这里直接给出EKF算法的实现过程，不对其进行理论推导，感兴趣的小伙伴可以参考相关的资料进行深入理解。 

4.EKF算法场景应用说明

        读到这里，相信大家肯定一头雾水，对EKF算法的实现过程即熟悉又陌生。我们究竟要如何实现上面的过程呢。为了使大家读完我的文章有所收获，这里我将通过具体的目标运动模型并结合雷达传感器探测过程来加深大家对EKF算法理解。

        假如我们有一个雷达传感器，该传感器可以观测到目标的径向距离r、方位角度θ和径向速度vr三个维度的信息。有一天，你拿着你的雷达到空旷的操场上玩耍，此时刚好在你雷达的视线范围内有一个匀速运动的目标，为了在二维坐标系下对该目标进行跟踪，你需要将雷达探测的信息转换至直角坐标系下，如图1所示，此时在笛卡尔坐标系下目标的状态可以使用下式进行描述：

式中和表示径向距离在x轴和y轴上的分量，和表示径向速度在x轴和y轴上的分量。

图1 笛卡尔坐标系与极坐标互换关系图

由于目标处于匀速运动状态，此时目标当前时刻的状态可以通过上一时刻的状态进行预测，即：

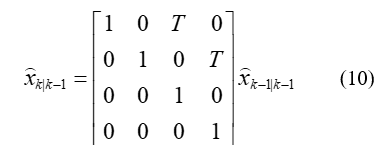
根据式(10)可以推断出该运动系统的状态转移矩阵为： 

现在我们已经有了目标的状态转移矩阵，似乎还缺乏观测矩阵。从前面我们知道，我们的雷达只能观测到目标的径向距离、方位角和径向速度。因此为了将目标的状态与观测的信息进行统一，我们不难列出系统的观测方程：

由式(12)可见，观测方程是一个非线性方程，因此需要通过式(3)进行求其雅可比观测矩阵。矩阵中的每一个元素对应h(x)中的每一个函数依次对每一个状态的偏导数。从式子(12)不难推出是一个维的矩阵，其每一个元素由下式进行计算： 

根据式(13)，并结合式(12)可以求得系统观测雅可比矩阵

        另外为什么我们要弄一个观测矩阵呢。我们观测式子（7）可以看到，我们需要通过估计的当前时刻的状态估算对应雷达观测的径向距离、方位角和径向速度,因此这个观测方程是必不可少的过程。如果条件可以，雷达传感器直接估计的参数与直角坐标系下的状态一致，此时观测矩阵H可以取值为单位矩阵。

        在状态转移矩阵和观测矩阵都确定后，接下来就是确定过程噪声协方差矩阵 Q 和观测噪声协方差矩阵 R。它们是平衡模型预测和观测数据信任度的核心参数。下面的表格展示了它们的物理意义和影响： 

6.EKF算法仿真实现

        根据上一节的描述，现在我们已经将该目标的各系统参量已经描述出来了，接下来就是将它们套入那五条该死的迷人的公式中进行滤波了，相信大家已经蠢蠢欲动了，那好让我们开始将上述过程通过程序描述出来吧。值得注意的是，博主仅提供了matalb仿真代码，如果各位小伙伴需要将其工程化，可以后台咨询博主，博主将会毫不吝啬的给予微薄的帮助。

       废话不多说直接上代码：

%%  Author  : Poulen
%%  Data    : 2025/5/7%% 卡尔曼滤波算法仿真
%% 仿真数据生成(加速目标运动数据为5m/s，数据采样为T/s一个点)
T = 40e-3;
frame = 200;%% 定义一个结构体数组
template = struct('Range', [], 'Azimuth', [], 'speed', []);
fixedData = repmat(template, 1, frame);          % 生成 1×frame 的结构体数组template = struct('rx', [], 'ry', [], 'vx', [],'vy',[]);
data = repmat(template, 1, frame);               % 生成 1×frame 的结构体数组
%% 模拟雷达测量的数据
R0      =200;   % 目标初始距离
Azimuth = 60;   % 此角度代表与x轴的夹角
v0      = -2;   % 目标初始速度for  i = 1 : frame%原始雷达测量数据（极坐标）fixedData(i).Range = R0 + (i-1)*T*v0 + unifrnd(-1.3, 1.3);fixedData(i).Azimuth = Azimuth + unifrnd(-5, 5);         % 均匀分布 [-2, 2];fixedData(i).speed   = v0 + unifrnd(-0.1, 0.1);%转化为直角坐标作为滤波输入data(i).rx =  fixedData(i).Range * cosd(fixedData(i).Azimuth);data(i).ry =  fixedData(i).Range * sind(fixedData(i).Azimuth);data(i).vx =  fixedData(i).speed * cosd(fixedData(i).Azimuth);data(i).vy =  fixedData(i).speed * sind(fixedData(i).Azimuth);  
end%% 卡尔曼滤波初始化矩阵F = [1  0   T   0;0  1   0   T;0  0   1   0;0  0   0   1];                 %状态转移矩阵Q = [T^4/4   0      T^3/4      0;0      T^4/4    0       T^3/4;T^3/2   0      T^2        0;0      T^3/2    0       T^2]; %过程噪声协方差矩阵R = [20   0    0;0   30    0;0   0    10]; %过程噪声协方差矩阵%状态初始化% 假设首次测量值
r0 = 190;       % 初始径向距离（米）
theta0 = 60;  % 初始水平角（45度）
vr0 = -2.8;       % 初始径向速度（米/秒）sigma_r = 1;        % 径向距离噪声标准差
sigma_vr = 0.5;     % 径向速度噪声标准差
sigma_theta = 0.1;  % 水平角噪声标准差% 初始状态估计
xt = [r0*cosd(theta0); r0*sind(theta0);vr0*cosd(theta0);vr0*sind(theta0)];
% 初始协方差矩阵
sigma_x = sqrt( (cos(theta0))^2 * sigma_r^2 + (r0*sin(theta0))^2 * sigma_theta^2 );
sigma_y = sqrt( (sin(theta0))^2 * sigma_r^2 + (r0*cos(theta0))^2 * sigma_theta^2 );
P = diag([sigma_x^2, sigma_y^2, 0, 0]);     % 速度初始方差设为0%% 定义一个用于接收kalman
template = struct('rx', [], 'ry', [], 'vx', [],'vy',[]);
data_filter = repmat(template, 1, frame);               % 生成 1×frame 的结构体数组I = eye(4,4);
for i = 1 : framez = [fixedData(i).Range;fixedData(i).Azimuth;fixedData(i).speed];%% 预测xt_ = F * xt;    % 预测P_  = F * P * F' + Q;%% 更新雅可比矩阵H = compute_H(xt_);%% kalman增益K  = P_*H'*(H*P_*H'+ R)^-1;x  = h_x(xt_)';xt = xt_ + K*(z -x);%% 更新P  = (I-K*H)*P_;%% 将滤波后的值保存data_filter(i).rx = xt(1);data_filter(i).ry = xt(2);data_filter(i).vx = xt(3);data_filter(i).vy = xt(4);
end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 可视化
figure;
h = scatter(data_filter(1).rx, data_filter(1).ry, 20, 'filled', 'MarkerFaceColor', 'b');  hold on; % 滤波结果 
g = scatter(data(1).rx, data(1).ry, 20, 'filled', 'MarkerFaceColor', 'r');   % 原始结果
axis([-300, 300, -100, 300]);
title('Radar Point Cloud Animation');
grid on;% 预创建文本标签对象（每个点三个标签：距离、角度、速度）
numPoints   = 1;
labelOffset = 20.0; % 标签偏移量（避免与点重叠）
textHandles = gobjects(numPoints, 3); % 存储文本句柄for i = 1:numPoints% 初始化三个标签（初始位置为 NaN 隐藏）textHandles(i,1) = text(NaN, NaN, '', 'Color', 'r', 'FontSize', 9, 'HorizontalAlignment', 'left');textHandles(i,2) = text(NaN, NaN, '', 'Color', 'black', 'FontSize', 9, 'HorizontalAlignment', 'left');textHandles(i,3) = text(NaN, NaN, '', 'Color', 'b', 'FontSize', 9, 'HorizontalAlignment', 'left');
end% 创建文本对象（初始内容为空）
txt = text(0.02, 0.95, '', 'Units', 'normalized', 'Color', 'r');            % 保存句柄% 逐帧更新
for k = 1:frame%计算目标距离、速度、角度z = [data_filter(k).rx;data_filter(k).ry;data_filter(k).vx;data_filter(k).vy];obj  = h_x(z);distance = obj(1);  % 滤波后的目标距离angle    = obj(2);  % 角度speed    = obj(3);  % 速度% 更新散点图的坐标数据set(h, 'XData', data_filter(k).rx, 'YData', data_filter(k).ry); set(g, 'XData', data(k).rx, 'YData', data(k).ry); % 更新所有点的标签for i = 1:numPointsx = data_filter(k).rx;y = data_filter(k).ry;% 设置标签内容distStr = sprintf('R:%.1fm', distance);angleStr = sprintf('A:%.1f°', angle);speedStr = sprintf('V:%.1fm/s', speed);% 更新标签位置和内容set(textHandles(i,1), 'Position', [x+labelOffset, y], 'String', distStr);set(textHandles(i,2), 'Position', [x+labelOffset, y-labelOffset*0.5], 'String', angleStr);set(textHandles(i,3), 'Position', [x+labelOffset, y-labelOffset*1.0], 'String', speedStr);end% 显示当前帧数set(txt, 'String', ['Frame: ', num2str(k)]);% 强制刷新图形并控制帧率drawnow limitrate;  % 高性能模式（比普通 drawnow 更快）% 可选：添加短暂暂停以同步实时显示
%     pause(0.0001); 
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function H = compute_H(x)x_pos = x(1);y_pos = x(2);vx = x(3);vy = x(4);r = sqrt(x_pos^2 + y_pos^2);vr = (x_pos*vx + y_pos*vy) / r;  % 径向速度% 避免除以零if r < 1e-6r = 1e-6;vr = 0;endH = zeros(3, 4);% 第1行：径向距离r对状态的偏导H(1, 1) = x_pos / r;H(1, 2) = y_pos / r;% 第2行：方位角θ对状态的偏导H(2, 1) = -y_pos / r^2;H(2, 2) = x_pos / r^2;% 第3行：径向速度v_r对状态的偏导H(3, 1) = (vx*r - x_pos*vr) / r^2;H(3, 2) = (vy*r - y_pos*vr) / r^2;H(3, 3) = x_pos / r;H(3, 4) = y_pos / r;
endfunction hx = h_x(x)x_pos = x(1);y_pos = x(2);vx = x(3);vy = x(4);r = sqrt(x_pos^2 + y_pos^2);vr = (x_pos*vx + y_pos*vy) / r;  % 径向速度% 避免除以零if r < 1e-6r = 1e-6;vr = 0;endhx(1) = r;hx(3) = vr;hx(2) = atand(y_pos/x_pos);
end

 仿真结果如图2所示：

图2 雷达目标跟踪结果

 

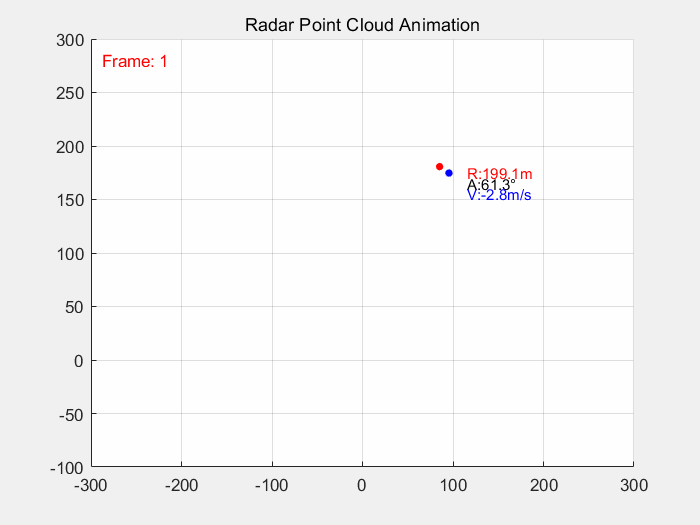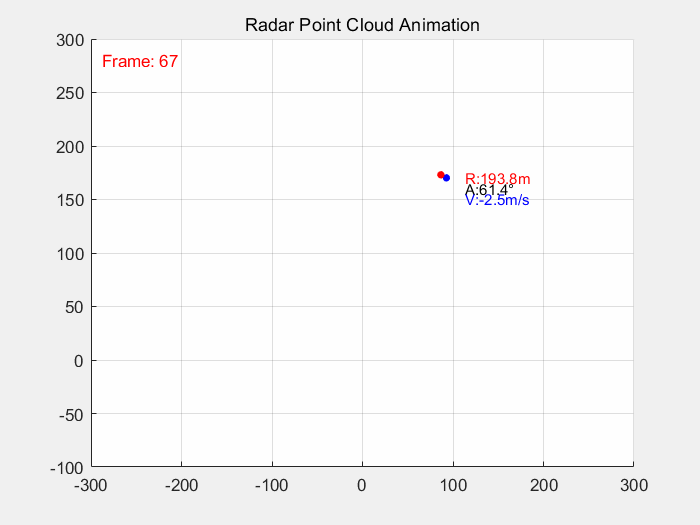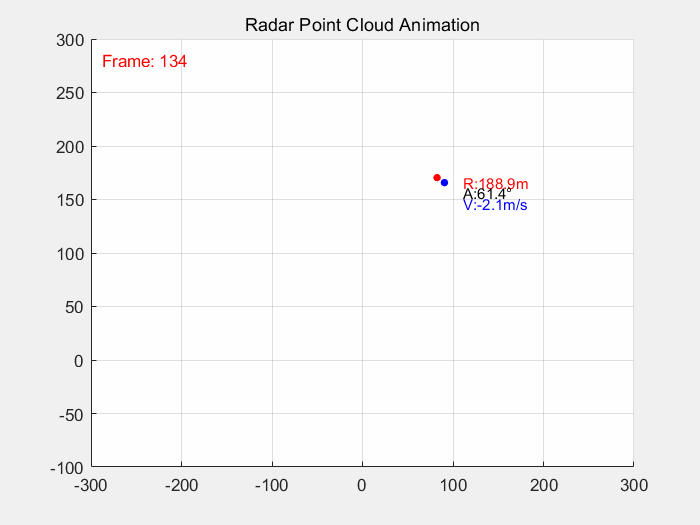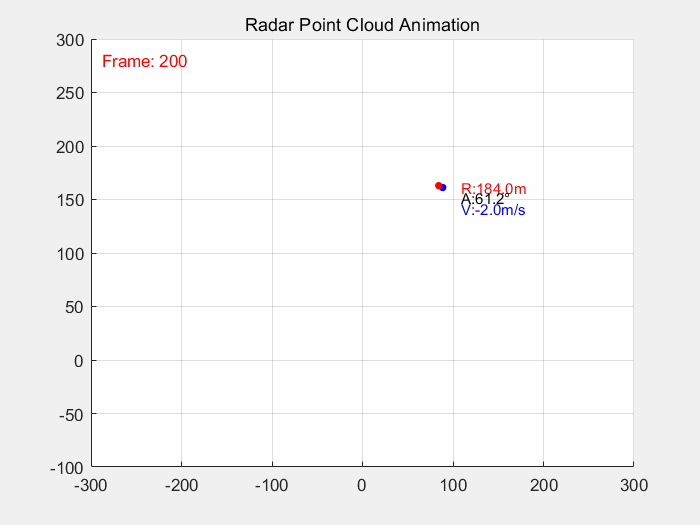
从图2所示的结果来看，蓝色点表示经过EKF滤波跟踪后的点，红色点表示原始观测点；从上图仿真结果可以很直观的看到目标经过EKF跟踪后目标轨迹变得稳定。

7.结束语

        本期为开源案例，后续我将持续更新雷达点云数据后处理的相关算法和仿真案例，希望本例程可以帮助到各位小伙伴。另外，本博文仅供学习参考，禁止未经允许进行转载等其它商业行为。如商业合作可后台私信博主。最后如果对你有帮助，希望各位可以点赞加个关注，毕竟你的支持就是我创作的最大动力。