Pinocchio导入URDF关节为continuous的问题及详细解释

视频讲解：

Pinocchio导入URDF关节为continuous的问题及详细解释

仓库地址：GitHub - LitchiCheng/mujoco-learning

问题背景：打算测试将之前的panda的urdf换成so-arm100的urdf，发现pinocchio的代码不能用，很奇怪，按照道理都是参数，应该可以直接复用，通过排查，发现时model.nq数量发生了变化，pyroboplan的代码在进行ik时直接越界了

   <jointname="Shoulder_Rotation"type="continuous"><originxyz="0 -0.0452 0.0181"rpy="1.5708 0 1.5708" /><parentlink="Base" /><childlink="Shoulder_Rotation_Pitch" /><axisxyz="0 1 0" /></joint>

进一步排查：

1.打印panda的model.nq发现和urdf中的关节数量一致，其type为revolute

2.打印so-arm100的model.nq发现比urdf中的joint多了一倍，其type为continuous

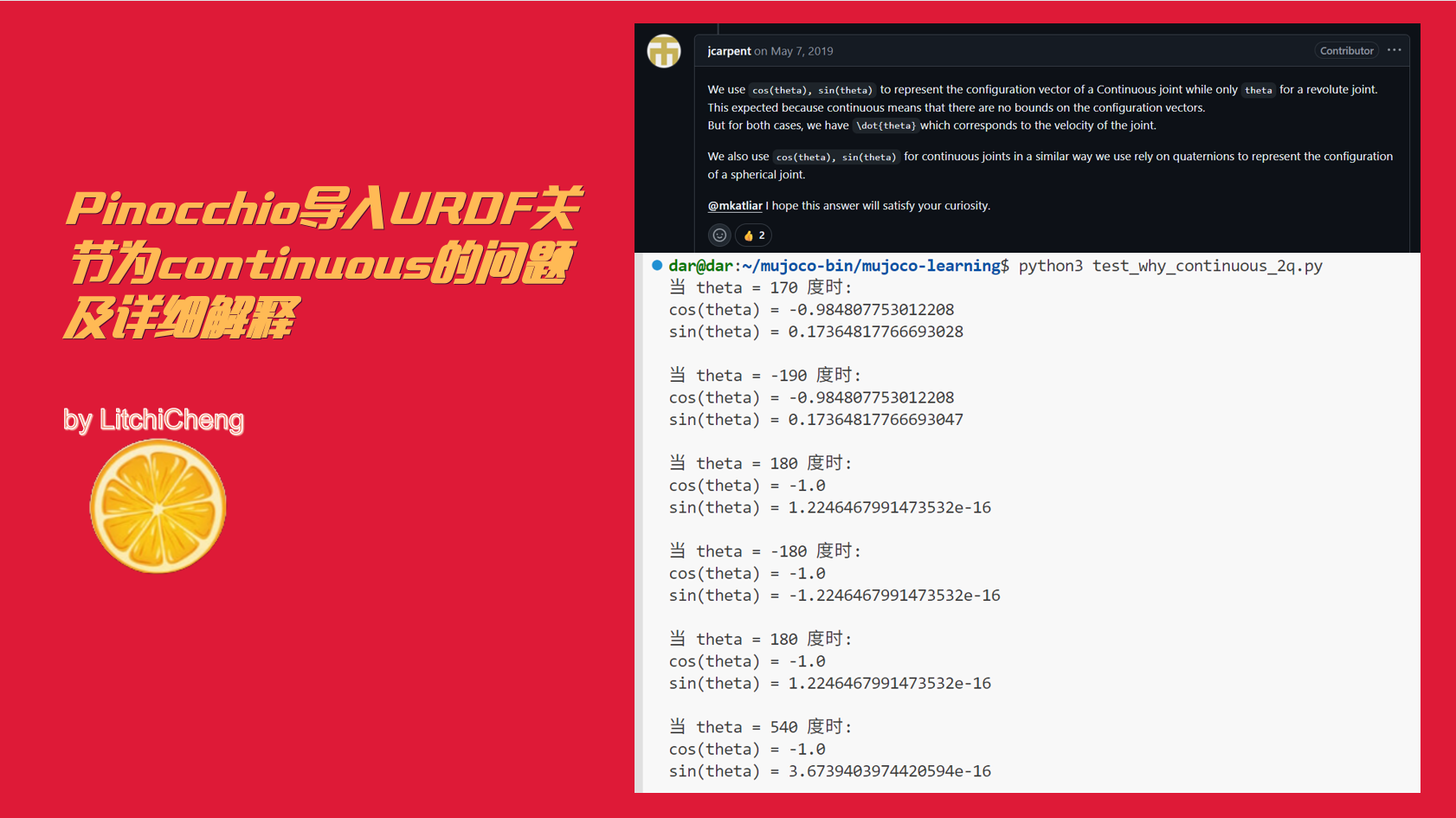
通过查看pinocchio的issues，发现如下两个解释：

Continuous joint in URDF adds 2 elements to the configuration space · Issue #794 · stack-of-tasks/pinocchio · GitHub

lowerPositionLimit and upperPositionLimit in pinocchio::Model have unexpected dimensions for unbounded joints - how to read them correctly? · Issue #777 · stack-of-tasks/pinocchio · GitHub

但实际上还没没有讲得很清楚为什么continous类型的joint的nq为2，这里进行探究：

URDF的continuous joint：本质也是一种无旋转角度限制的旋转关节（unbounded revolute joint），理论上应使用单个角度参数θ描述其状态就够了，但是为什么需要用两个，这就要反过来思考了，首先1个配置空间的维度能不能用来描述continuous类型关节对应物理位置，肯定是够了，但会出现一种情况，如关节在θ时和θ+2Π实际上物理位置一致，有无数个数值对应同样的物理位置，对于优化、求解问题来说时冗余的

所以用从如下两个角度可以理解[cosθ, sinθ]的好处：

1.一个数值对对应了一个物理状态，避免求解的冗余问题

2.cosθ和sinθ避免2Π到0的跳跃

下面用python代码来做一个验证

import math
# 定义角度
angles = [170, -190, 180, -180, 180, 540]# 遍历角度列表
for theta in angles:# 将角度转换为弧度theta_rad = math.radians(theta)# 计算 cos 和 sin 值cos_theta = math.cos(theta_rad)sin_theta = math.sin(theta_rad)# 输出结果print(f"当 theta = {theta} 度时:")print(f"cos(theta) = {cos_theta}")print(f"sin(theta) = {sin_theta}")print()

可以看到三种情况下数值对均一致

1.170和反方向

2.180°和反向180

3.180和多转一圈