当前位置：首页 > news >正文

matlab学习之旅

news 来源：原创 2025/5/4 8:50:51

一、矩阵操作

创建一个 3×3 的随机矩阵 A，元素范围为 [0, 10]（包含 0 和 10）。
计算矩阵 A 的转置矩阵，并存储到矩阵 B 中。
求矩阵 A 的行列式值，并判断矩阵 A 是否可逆（行列式不为零则可逆）。
若矩阵 A 可逆，计算其逆矩阵并存储到矩阵 C 中；若不可逆，输出提示信息“矩阵 A 不可逆”。

代码

% 1. 创建一个3x3的随机矩阵A，元素范围为[0, 10]
A = randi([0, 10], 3, 3);% 显示矩阵A
disp('矩阵A:');
disp(A);% 2. 计算矩阵A的转置矩阵，并存储到矩阵B中
B = A';
disp('矩阵A的转置矩阵B:');
disp(B);% 3. 求矩阵A的行列式值，并判断矩阵A是否可逆
detA = det(A);
disp(['矩阵A的行列式值: ', num2str(detA)]);if detA == 0disp('矩阵A不可逆');
elsedisp('矩阵A可逆');% 4. 若矩阵A可逆，计算其逆矩阵并存储到矩阵C中C = inv(A);disp('矩阵A的逆矩阵C:');disp(C);
end

运行结果
在这里插入图片描述

二、多项式计算

定义一个多项式 p(x)=2x4+3x3−5x2+7x−1。
计算多项式在 x=2 处的值。
求多项式的导数，并存储为多项式q(x)。
求多项式 p(x) 的根（可能包含复数根）。

代码

% 定义多项式 p(x) = 2x^4 + 3x^3 - 5x^2 + 7x - 1
p = [2 3 -5 7 -1]; % 多项式系数，按降幂排列% 1. 计算多项式在 x=2 处的值
x = 2;
p_value_at_2 = polyval(p, x);
fprintf('p(2) = %f\n', p_value_at_2);% 2. 求多项式的导数，存储为 q(x)
q = polyder(p); % 对多项式 p 求导
disp('导数多项式 q(x) 的系数:');
disp(q);% 3. 求多项式 p(x) 的根（可能包含复数根）
roots_p = roots(p);
disp('多项式 p(x) 的根:');
disp(roots_p);

运行结果
在这里插入图片描述

三、函数、循环和条件语句

编写一个函数 sumSquares(n)，输入参数为正整数 n，输出从 1 到 n 的所有整数的平方和，即 12+22+…+n2。
编写一个脚本，使用循环结构（for 或 while）和条件语句，实现以下功能：
 输入一个正整数 m。
 判断 m 是否为素数。如果是素数，输出“m 是素数”；否则，输出“m 不是素数”。
 如果 m 不是素数，找出其所有正因数（不包括 1 和 m 本身）并输出。
代码1

function result = SumSquares(n)% 检查输入是否为正整数if ~isscalar(n) || n <= 0 || mod(n, 1) ~= 0error('输入必须是正整数');end% 计算从1到n的所有整数的平方和result = sum((1:n).^2);
end

运行结果1
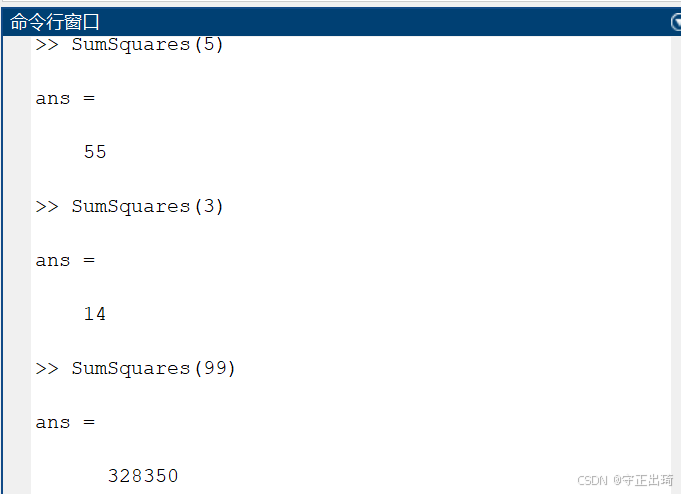
在这里插入图片描述

代码2

% 输入一个正整数 m
m = input('请输入一个正整数: ');% 检查输入是否为正整数
if ~isscalar(m) || m <= 0 || mod(m, 1) ~= 0error('输入必须是正整数');
end% 定义一个函数来判断是否为素数
function isPrime = checkPrime(num)if num <= 1isPrime = false;return;endfor i = 2:sqrt(num)if mod(num, i) == 0isPrime = false;return;endendisPrime = true;
end% 判断 m 是否为素数
if checkPrime(m)disp(['m 是素数']);
elsedisp(['m 不是素数']);% 找出所有正因数（不包括 1 和 m 本身）factors = [];for i = 2:m-1if mod(m, i) == 0factors = [factors, i];endendif ~isempty(factors)disp('m 的正因数有:');disp(factors);elsedisp('m 没有其他正因数');end
end