当前位置：首页 > news >正文

贝叶斯算法（Bayesian Algorithms）详解

news 来源：原创 2025/5/3 9:06:01

引言

贝叶斯算法是一类基于贝叶斯定理的概率统计方法，核心思想是通过先验概率和观测数据计算后验概率，从而进行预测或决策。它广泛应用于分类、回归、推荐系统、自然语言处理等领域。

1. 贝叶斯定理（Bayes’ Theorem）

贝叶斯定理是概率论中的核心公式，描述了在已知某些条件下，事件发生的概率如何更新：
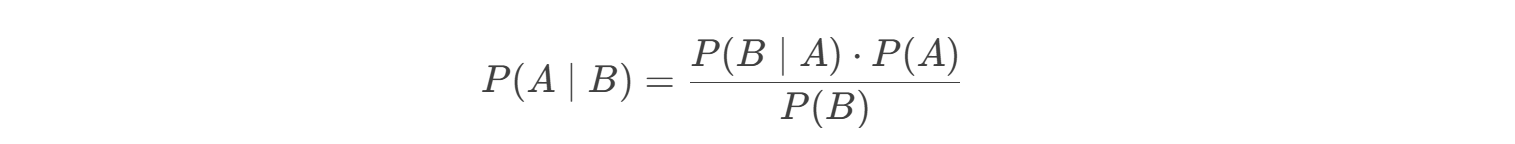
在这里插入图片描述

其中：

( P(A | B) )：后验概率（在观测到 ( B ) 后，( A ) 发生的概率）。
( P(B| A) )：似然概率（在 ( A ) 发生时，( B ) 出现的概率）。
( P(A) )：先验概率（( A ) 的初始概率，基于历史数据或经验）。
( P(B) )：边缘概率（( B ) 发生的总概率）。

2. 贝叶斯算法的核心思想

利用先验知识：通过已有数据或经验设定初始概率（先验）。
逐步更新信念：结合新数据计算后验概率，动态调整模型。
处理不确定性：输出概率分布而非确定值，适合需要量化置信度的场景。

3. 贝叶斯算法的分类

贝叶斯方法可分为以下几类：

(1) 生成式模型 vs 判别式模型

类型	代表算法	特点
生成式模型	朴素贝叶斯、高斯混合模型	学习数据的联合分布 ( P(X, Y) )，可生成新样本（如文本生成）。
判别式模型	逻辑回归、SVM	直接学习决策边界 ( P(Y \mid X) )，通常分类效果更好，但不能生成数据。

(2) 常见贝叶斯算法

算法	适用任务	数据要求	典型应用
朴素贝叶斯	分类	离散特征（如文本）	垃圾邮件过滤、情感分析
贝叶斯线性回归	回归	连续特征	房价预测（带不确定性估计）
高斯过程回归	回归/分类	连续特征	时间序列预测、机器人控制
隐马尔可夫模型	序列预测	时序数据	语音识别、基因序列分析
贝叶斯网络	概率推理	结构化数据（因果关系）	医疗诊断、风险评估

4. 朴素贝叶斯（Naive Bayes）

朴素贝叶斯是最常用的贝叶斯分类器，基于“特征条件独立”的强假设（因此称为“朴素”）。

(1) 公式推导

对于输入特征x = (x_1, x_2, …, x_n) )，预测类别 ( y ) 的后验概率：
在这里插入图片描述

其中：

( P(y) )：类别的先验概率（训练集中各类的频率）。
( P(x_i | y) )：特征 ( x_i ) 在类别 ( y ) 下的条件概率。

(2) 变种与适用场景

变种	数据分布假设	适用场景
MultinomialNB	多项式分布（离散计数）	文本分类（词频统计）
GaussianNB	高斯分布（连续值）	医学诊断、传感器数据
BernoulliNB	伯努利分布（二值特征）	垃圾邮件检测（单词是否出现）

(3) 代码示例（文本分类）

from sklearn.naive_bayes import MultinomialNB
from sklearn.feature_extraction.text import CountVectorizer# 训练数据
corpus = ["good movie", "bad movie", "great film", "poor film"]
labels = ["pos", "neg", "pos", "neg"]# 文本 → 词频矩阵
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(corpus)# 训练模型
model = MultinomialNB(alpha=1.0)  # Laplace平滑
model.fit(X, labels)# 预测新样本
new_text = ["good film"]
X_new = vectorizer.transform(new_text)
print(model.predict(X_new))  # 输出: ['pos']

5. 贝叶斯回归（Bayesian Regression）

与传统线性回归不同，贝叶斯回归将模型参数（如权重 ( \mathbf{w} )）视为随机变量，通过先验分布和数据更新后验分布。

(1) 公式推导

在这里插入图片描述

(2) 代码示例（Scikit-Learn）

from sklearn.linear_model import BayesianRidge# 训练数据
X = [[1], [2], [3], [4]]
y = [1, 2, 3, 4]# 训练模型
model = BayesianRidge()
model.fit(X, y)# 预测（返回均值和标准差）
y_pred, y_std = model.predict([[5]], return_std=True)
print(f"预测值: {y_pred[0]:.2f} ± {y_std[0]:.2f}")  # 输出: 5.00 ± 0.71

6. 贝叶斯算法的优缺点

优点

处理小样本数据：通过先验知识补充数据不足。
量化不确定性：输出概率分布（如置信区间）。
在线学习：可逐步更新模型（适合流式数据）。

缺点

计算复杂度高：尤其是高维数据（MCMC采样耗时）。
依赖先验设定：错误的先验会导致偏差。
朴素贝叶斯的强假设：特征独立性可能不成立。

7. 应用场景

领域	具体应用
自然语言处理	文本分类（朴素贝叶斯）、机器翻译（贝叶斯网络）
医疗诊断	疾病预测（贝叶斯网络）、药物研发（高斯过程）
推荐系统	协同过滤（概率矩阵分解）
金融风控	信用评分（贝叶斯逻辑回归）、欺诈检测（异常检测）
计算机视觉	图像分割（马尔可夫随机场）、目标检测（贝叶斯深度学习）

8. 总结

贝叶斯方法的核心：通过概率建模结合先验与数据，提供可解释的预测。
常用算法：
- 分类：朴素贝叶斯（MultinomialNB/GaussianNB）。
- 回归：贝叶斯线性回归、高斯过程。
- 复杂推理：贝叶斯网络、MCMC采样。
适用场景：小样本、需不确定性量化、动态更新模型的场景。