【学习笔记】第十章：序列建模：递归神经网络（RNN）

作者选择了由 Ian Goodfellow、Yoshua Bengio 和 Aaron Courville 三位大佬撰写的《Deep Learning》(人工智能领域的经典教程，深度学习领域研究生必读教材),开始深度学习领域学习，深入全面的理解深度学习的理论知识。

之前的文章参考下面的链接：
【学习笔记】理解深度学习和机器学习的数学基础：数值计算
【学习笔记】理解深度学习的基础：机器学习
【学习笔记】深度学习网络-深度前馈网络（MLP）
【学习笔记】深度学习网络-正则化方法
【学习笔记】深度学习网络-深度模型中的优化
【学习笔记】卷积网络简介及原理探析

引言

递归神经网络（Recurrent Neural Networks, RNN）是一类专门用于处理序列数据的神经网络。与卷积神经网络（CNN）主要针对二维网格数据（如图像）的应用不同，RNN 专注于处理一维序列数据（如时间序列、文本等）。RNN 的设计使其能够有效捕捉时间序列中的时序信息，广泛应用于各类任务，包括自然语言处理、时间序列预测和语音识别。本章将深入探讨 RNN 的基本原理、结构、训练方法及其在实际应用中的表现。

10.1 计算图的展开

计算图是对计算过程的结构化表示，展示了输入、参数和输出之间的关系。在 RNN 中，通过展开计算图，将递归计算转化为具有效率的重复结构，使得参数可以被共享。这种方法在处理可变长度的序列时非常有效。在经典动态系统中，递归的表达形式为：

$$s(t)=f(s(t-1);\theta )$$

其中 (s(t)) 是系统的状态，(\theta) 是需要学习的参数。通过对方程进行多步展开，我们得到：

$$s(3)=f(s(2);\theta )=f(f(s(1);\theta );\theta )$$

这种展开使得我们能够更好地理解信息流的前向传播和后向传播。同时，它便于计算梯度，优化网络参数。

10.2 递归神经网络

基于图的展开和参数共享的思想，我们可以设计多种不同类型的递归神经网络。以下是一些常见的设计模式：

• 逐步输出递归网络：在每个时间步都有输出，且隐含层之间具有递归连接。
• 层次递归网络：从前一时间步的输出连接到当前隐藏单元的递归网络。
• 序列输出递归网络：读取整个序列后，仅在最后生成一个输出。

10.2.1 RNN 的基本结构

一个典型的 RNN 由输入层、隐含层和输出层组成，其基本结构可通过以下数学模型描述：

隐含状态更新公式为：

$$h(t)=f(Wh(t-1)+Ux(t))$$

其中：

• (W) 是隐含层的递归权重。
• (U) 是输入到隐含层的权重。

输出的生成公式为：

$$o(t)=g(Vh(t))$$

其中：

• (g) 是输出层的激活函数。
• (V) 是隐含层到输出层的权重。

这种结构使得 RNN 能够有效地处理序列数据，将先前的信息状态与当前输入结合，以生成新的输出。

10.2.2 训练过程

RNN 的训练通常采用反向传播通过时间（Backpropagation Through Time, BPTT）算法。BPTT 的基本流程如下：

1. 展开 RNN 的计算图。
2. 计算每个时间步的损失函数 (L(t))，常用的损失函数为交叉熵损失。
3. 利用梯度信息更新权重。

这种训练方法通过序列中每个时刻的信息流来逐步调整模型参数，从而提高模型的预测能力。

10.3 条件递归神经网络

条件递归神经网络在标准 RNN 的基础上增加了从上一个输出到当前状态的连接。这一设计使得网络能够模拟更复杂的关系，建模任意分布的序列 (y) 提高了模型的表达能力。

10.3.1 条件建模公式

条件概率分布可表示为：

$$P(y|x)=f(h(x))$$

其中，(h(x)) 是输入序列的隐含表示。这一结构使得 RNN 可以在处理给定输入序列 (x) 时，生成相应的输出序列 (y)。

10.4 编码器-解码器架构

编码器-解码器架构是 RNN 中的一种重要应用，通常由两个 RNN 组成：一个用于处理输入序列（编码器），另一个用于生成输出序列（解码器）。

10.4.1 工作流程

在编码器-解码器架构中，编码器首先处理输入序列，并生成一个上下文向量 (C)，该向量包含了输入序列的核心信息。解码器则利用这个上下文向量生成最终的输出序列 (Y)。这一设计广泛应用于诸如机器翻译、文本生成等领域，实现了从一种语言到另一种语言的有效转化。

10.5 长期依赖问题

尽管 RNN 在处理序列数据方面表现优异，但是训练 RNN 学习长期依赖时仍然面临困难。这主要是由于在反向传播过程中，梯度可能会迅速消失或爆炸，导致模型难以捕捉远期信息。

此处绘制从 100 维隐藏状态降到单个维度的线性投影，绘制于 y 轴上。x 轴是 100 维空间中沿着随机方向的初始状态的坐标。因此，我们可以将该图视为高维函数的线性截面。曲线显示每个时间步之后的函数，或者等价地，转换函数被组合一定次数之后。

10.5.1 解决方案

为了应对这一问题，研究者们提出了长短期记忆网络（LSTM）和门控循环单元（GRU）等网络结构。这些结构通过引入门控机制，有效解决了长期依赖问题，使得模型能够学习长序列中的重要信息。

10.6 回声状态网络（ESN）

回声状态网络是一种特殊类型的 RNN，其特点是将循环权重设为固定，只对输出权重进行学习。这种方法避免了 RNN 训练中的复杂性，让模型能以简化的方式提取序列数据的特征。

10.6.1 结构和优势

ESN 采用随机固定的连接，使其能够产生丰富的动态响应。通过仅学习从隐藏状态到输出的线性映射，极大地简化了训练过程。这种网络主要用于捕捉时间序列中的短期变化，能够在许多应用场景中表现出色。

10.7 显式记忆

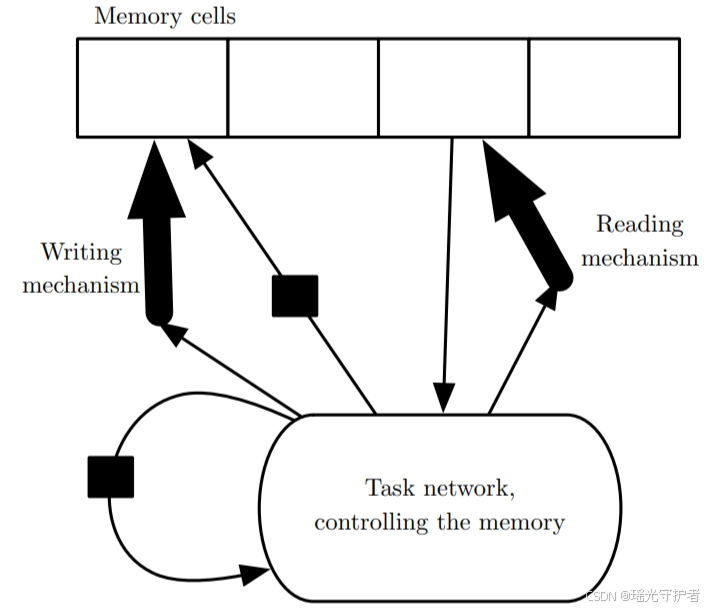
显式记忆的引入使得 RNN 能够存储和检索特定信息，从而极大提升了模型的智能水平。记忆网络（Memory Networks）和神经图灵机（Neural Turing Machines）就是实现这一目标的两种方法。

10.7.1 基本原理

• 记忆网络：设计包含一组可通过寻址机制访问的记忆单元，允许网络在需要的时候调用历史信息。
• 神经图灵机：具备读取和写入任意内容到记忆单元的能力，使网络能高效地进行复杂计算。

10.8 总结

递归神经网络作为一种强大的序列建模工具，因其出色的表达能力被广泛应用于自然语言处理、时间序列预测等领域。尽管训练 RNN 存在一定的挑战，但通过 LSTM、GRU 等先进结构的应用结合显式记忆的概念，可以有效提升模型的性能与适应性。

通过深入学习 RNN 及其变体的运作原理，以及在不同应用场景中的表现，我们能够更好地理解这一强大工具的潜力与未来发展方向。随着技术的进步，RNN 在序列数据中的应用将越来越广泛，为各类实际问题的解决提供更多可能性。