神经网络入门
文章目录
- 前言
- 一、神经元
- 1. 神经元的主要部分
- 2. 信息传递过程
- 3. 类比人工神经元
- 二、神经网络层
- 1. 输入层(Input Layer)
- 2. 隐藏层(Hidden Layer / 全连接层 Dense Layer)
- 3. 输出层(Output Layer)
- 三、偏置与权重参数
- 1. 权重(Weights)
- 2. 偏置(Bias)
- 3、参数更新机制
- 四、激活函数
- 1. 激活函数的作用
- (1)引入非线性
- (2)控制输出范围
- (3)决定神经元激活状态
- 2. 常见的激活函数
- (1)Sigmoid
- (2)Tanh(双曲正切)
- (3)ReLU(修正线性单元)
- 总结
前言
神经网络入门是理解人工智能的核心基础,它通过模拟人脑神经元的工作方式,构建多层连接的数学模型,学习从数据中提取特征并进行预测。简单来说,神经网络由输入层接收数据(如图像或文本),经过隐藏层逐层加权计算和非线性激活,最终由输出层给出结果(如分类或预测)。入门可从感知机、激活函数、反向传播等基础概念入手,逐步掌握其在图像识别、自然语言处理等场景的应用逻辑。
神经网络的基本结构是由输入层接收数据,通过隐藏层中的加权连接和激活函数进行非线性变换,最终由输出层生成预测结果的多层互联节点网络。
一、神经元

1. 神经元的主要部分
(1)细胞体(Soma)
作用:整合输入信号,决定是否触发动作电位(电脉冲)。关键结构:细胞核、线粒体等,维持神经元代谢活动。
(2)树突(Dendrites)
作用:接收其他神经元传来的化学信号,将其转换为电信号(突触后电位)。特点:分支多、表面积大,增强信号接收能力。
(3)轴突(Axon)
作用:将细胞体产生的动作电位(电信号)长距离传递至轴突末梢。特点:部分轴突包裹髓鞘(由施万细胞形成),加速电信号传导(跳跃式传导)。
(4)轴突末梢(Axon Terminal)
作用:将电信号转换为化学信号(释放神经递质),通过突触传递给下一神经元。
(5)突触(Synapse)
作用:神经元间的连接点,由突触前膜(释放递质)、突触间隙(递质扩散)和突触后膜(受体接收)组成。
2. 信息传递过程
信号接收:树突接收其他神经元的神经递质,引发局部电位变化(突触后电位)。信号整合:细胞体整合所有突触后电位,若总和超过阈值,触发动作电位(全或无原则)。电信号传导:动作电位沿轴突快速传导(依赖钠/钾离子通道的开闭)。化学信号传递:轴突末梢的突触小泡释放神经递质(如多巴胺、谷氨酸),进入突触间隙。信号接收端:递质与下一神经元的突触后膜受体结合,引发新的电信号(完成跨神经元传递)。
3. 类比人工神经元
树突 → 输入权重(接收信息)。细胞体整合信号 → 加权求和 + 激活函数(决定是否“激活”)。轴突 → 输出信号传递。突触可塑性(强弱变化)→ 人工神经网络中的权重调整。
生物神经元通过电-化学信号的复杂协作,实现了高效、动态的信息传递,这一机制启发了人工神经网络的设计。
二、神经网络层

1. 输入层(Input Layer)
输入层是网络的“数据入口”,负责接收未经处理的原始数据(如图像像素、文本向量、传感器读数等)。每个节点对应输入数据的一个特征(例如一张28×28像素的图片展开为784个节点),仅传递数据而不进行任何计算。输入层的维度直接由数据的结构决定,例如在房价预测任务中,输入层节点数可能等于房屋特征的数量(如面积、房间数等)。
2. 隐藏层(Hidden Layer / 全连接层 Dense Layer)
隐藏层是网络的核心计算单元,通过加权求和(z=Wx+b)与激活函数对输入数据进行非线性变换。每个神经元接收上一层的所有输出并赋予不同权重,整合后通过激活函数(如ReLU、Sigmoid)决定是否“激活”(输出信号)。隐藏层的节点数和层数可自由设计:
浅层网络:1-2层隐藏层,适合简单任务。深层网络:多个隐藏层,逐层提取高阶特征(如从图像边缘到物体形状)。例如,一个包含128个节点的隐藏层可将输入特征映射到更高维空间,增强模型的表达能力。
3. 输出层(Output Layer)
输出层是网络的“结果出口”,根据任务类型生成最终预测:
分类任务:节点数等于类别数,使用 Softmax 激活函数输出概率分布(如手写数字识别输出0-9的概率)。回归任务:单节点直接输出连续值(如预测温度、房价),通常不使用激活函数或仅用线性激活。二分类:单节点 + Sigmoid 函数,输出0~1的概率值(如判断是否为垃圾邮件)。
三、偏置与权重参数

观察上图,其中x1和x2是神经网络的输入,1就是偏置项,w1、w2、w3则是神经网络的权重参数,sigmoid是激活函数的一种,最终输出结果,上面就是一个神经元的基本结构。
1. 权重(Weights)
定义:权重是连接神经网络中相邻层节点的参数,用于调节输入信号对下一层的影响程度。
作用:
决定每个输入特征的重要性。例如,在预测房价时,“面积”特征的权重可能远大于“楼层”特征的权重。通过加权和(z=W⋅x)将输入数据线性组合,为后续非线性变换提供基础。
特点:
每个连接(边)对应一个独立权重。训练过程中通过反向传播调整权重,使网络逐步逼近目标函数。权重初始化策略(如Xavier、He初始化)影响训练速度和模型性能。
2. 偏置(Bias)
定义:偏置是每个神经元(节点)的附加参数,用于调整输出结果的偏移量。
作用:
在加权和(z=W⋅x+b)中提供基线偏移,使激活函数的输出更灵活。在没有输入信号时(x=0),偏置直接决定神经元是否被激活(如 b>0 时,ReLU可能输出非零值)。
特点:
每个神经元对应一个独立偏置。偏置的调整允许模型适应数据中的系统性偏差(如分类任务中正负样本不平衡)。
3、参数更新机制
训练目标:通过优化算法(如梯度下降)调整权重和偏置,最小化损失函数。

关键意义:权重和偏置是神经网络中的两个参数,是需要不断调整来使神经网络的预测效果提升的重要参数,权重和偏置的调整是神经网络学习的本质,决定了模型从数据中提取规律的能力。
四、激活函数
1. 激活函数的作用
激活函数是神经网络中实现非线性变换的核心组件,其核心作用包括:
(1)引入非线性
问题:如果神经网络只有线性运算(加权求和),无论叠加多少层,整体仍等效于单层线性模型,无法拟合复杂函数(如分类边界、图像特征等)。
解决:激活函数对加权和进行非线性映射(如ReLU、Sigmoid),使网络能够学习任意复杂的输入-输出关系。
(2)控制输出范围
限制输出范围:例如:
Sigmoid将输出压缩到 [0, 1],适合概率预测。
Tanh将输出限制到 [-1, 1],解决Sigmoid的对称性问题。
稳定梯度:某些激活函数(如Tanh)的梯度更平缓,有助于缓解训练中的梯度爆炸或消失。
(3)决定神经元激活状态
“激活”或“抑制”:通过阈值机制(如ReLU在输入≤0时输出0)过滤信号,模拟生物神经元的“全或无”特性。
稀疏性:ReLU等函数可使部分神经元输出为0,提升网络的计算效率。
2. 常见的激活函数
(1)Sigmoid
公式:

输出范围:0~1

特点:
早期广泛使用,适合二分类输出层(概率解释)。
缺点:
梯度消失:当输入绝对值较大时,梯度接近0,导致深层网络难以训练。输出非零中心化:可能影响梯度下降效率。
应用场景:二分类输出层、传统神经网络隐藏层(现较少使用)。
(2)Tanh(双曲正切)
公式:
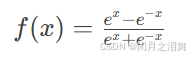
输出范围:-1~1

特点:
输出以0为中心,梯度下降效率优于Sigmoid。梯度消失问题依然存在,但比Sigmoid略轻。
应用场景:RNN、某些隐藏层。
(3)ReLU(修正线性单元)
公式: 
输出范围:0~+∞

特点:
优点:计算高效(无指数运算);缓解梯度消失(正区间梯度恒为1)。缺点:“死亡神经元”,输入≤0时梯度为0,神经元永久失活。
应用场景:深度学习隐藏层的默认选择(如CNN、全连接网络)。
总结
本章介绍了神经网络的一些基本概念,随着不断地学习,你会发现不同的神经网络的本质都是相同的,都是由最基础的神经网络搭建起来的,不同的神经网络处理同一问题的效果也是不同的,因此在解决实际问题时,需要根据问题本身选择合适的神经网络。
