2025五一数学建模竞赛B题完整分析论文(共42页)(含模型、可运行代码、数据)
2025年五一数学建模竞赛B题完整分析论文
摘 要
一、问题分析
二、问题重述
三、模型假设
四、符号定义
五、 模型建立与求解
5.1问题1
5.1.1问题1思路分析
5.1.2问题1模型建立
5.1.3问题1代码
5.1.4问题1求解结果
5.2问题2
5.2.1问题2思路分析
5.2.2问题2模型建立
5.2.3问题2代码
5.2.4问题2求解结果
5.3问题3
5.3.1问题3思路分析
5.3.2问题3模型建立
5.3.3问题3代码
5.3.4问题3求解结果
5.4问题4
5.4.1问题4思路分析
5.4.2问题4模型建立
5.4.3问题4代码
5.4.4问题4求解结果
5.5问题5
5.5.1问题5思路分析
5.5.2问题5模型建立
5.5.3问题5代码
5.5.4问题5求解结果
六、 模型推广
2025五一数学建模B题助攻资料下载
链接: 百度网盘 请输入提取码 提取码: tifs
2025五一数学建模B题助攻资料下载
链接: 百度网盘 请输入提取码 提取码: tifs
摘 要
随着矿山监测数据的不断增加和多样化,如何高效处理这些大规模、高维数据成为了一个重要问题。数据变换、压缩、去噪和降维重构等技术不仅能提高数据存储和计算效率,还能提升模型的预测精度。本论文针对矿山监测数据中的多个关键问题,提出了有效的数学建模方法,涵盖了数据预处理、降维、变换及模型优化等多个方面,为矿山监测领域提供了可靠的解决方案。
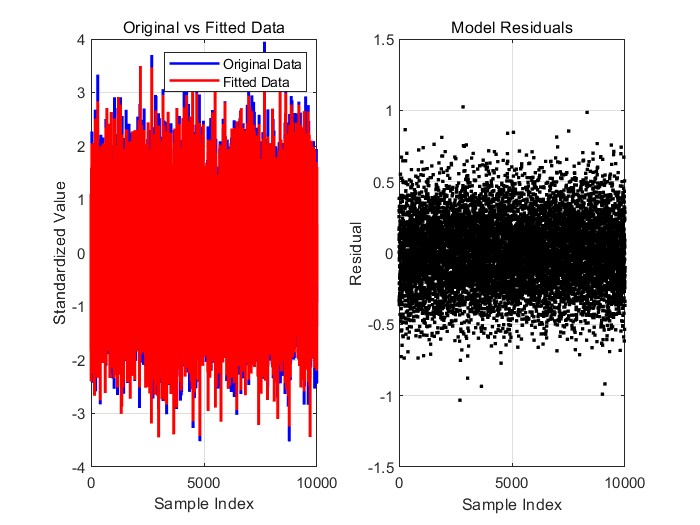
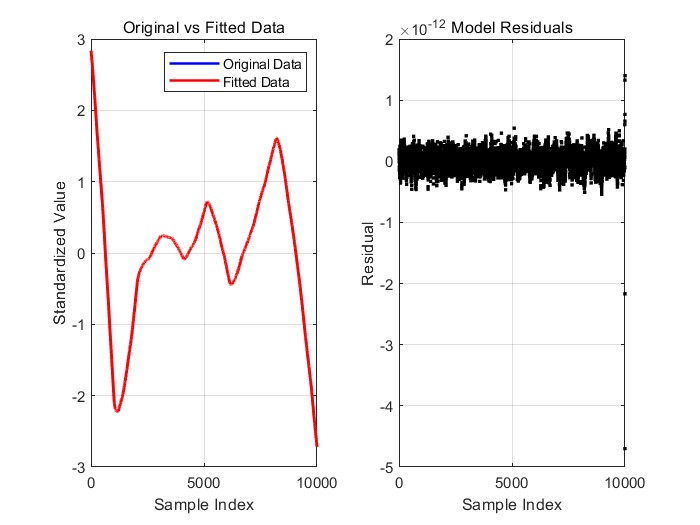
问题一中,我们针对附件1中的数据A,通过建立数学模型进行数据变换,优化变换后的数据结果,使其尽可能接近原始数据。我们通过计算变换后的数据与原数据之间的误差,并分析了数据噪声和模型偏差对结果的影响,最终得出有效的误差控制方案,确保了变换数据的准确性,并为后续分析提供了可靠的数据基础。
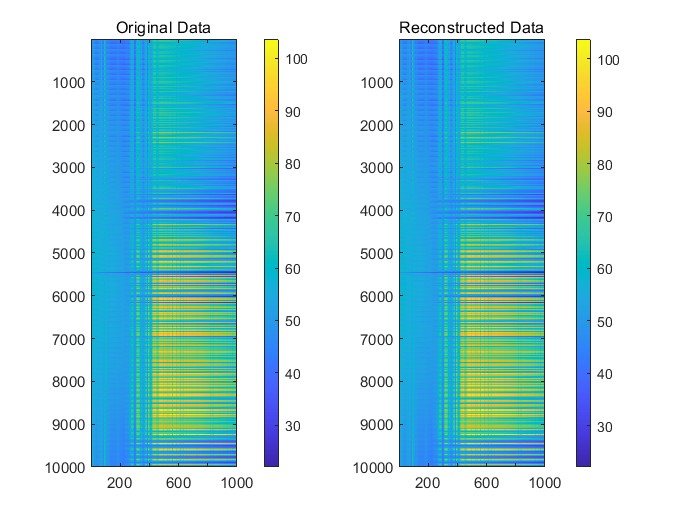
问题二中,我们建立了数据压缩模型,并对附件2中的矿山监测数据进行了降维处理。在保证数据还原准确度(MSE不高于0.005)的前提下,我们计算了压缩比和存储空质量的影响,最终得到间节省率,分析了降维与还原对数据了较高的压缩效率和良好的还原效果,验证了降维方法在数据压缩和存储优化中的有效性。
问题三中,我们处理了矿山监测数据中的噪声问题,使用去噪和标准化方法对数据X进行预处理。随后,建立了X与目标变量Y之间的关系模型,并通过拟合优度的计算和统计检验,确保了模型具有较强的解释能力和稳定性,从而使得模型能够准确预测和解释数据之间的关系,为数据分析提供了更加稳健的支持。
问题四中,我们设计了一个自适应调整算法来优化模型的超参数,并建立了X与Y之间的关系模型。通过计算平均预测误差和评估模型的稳定性,我们成功提高了模型的拟合优度,并验证了模型在不同数据集上的适用性,确保了其良好的泛化能力,进一步提升了预测效果和模型的适用性。
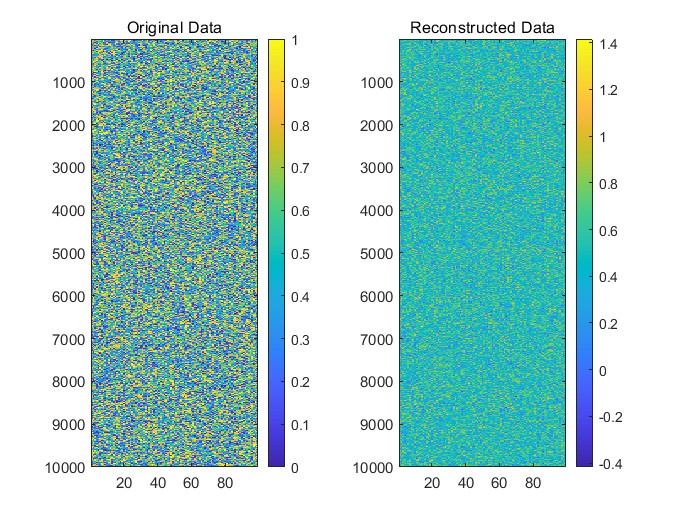
问题五中,我们对附件5中的高维数据进行了降维处理,并建立了一个重构模型,通过降维数据恢复原始数据的主要特征。通过分析降维与重构之间的平衡关系,评估了重构数据与目标变量Y之间的关系模型,并对模型的泛化能力和计算复杂度进行了分析,验证了该方法在高维数据处理中的高效性,解决了数据处理过程中的计算瓶颈问题。
本文通过对矿山监测数据的多角度分析,成功提出了数据降维、重构、去噪和模型优化的解决方案,并为相关领域的研究提供了宝贵的思路和方法。通过优化数据处理流程,本文不仅提高了数据的处理效率,也增强了模型的预测能力,为矿山监测数据的深入分析和实际应用提供了可靠的理论基础和技术支持。
关键词:数据变换 数据压缩 去噪 自适应调整 降维重构
2025五一数学建模B题助攻资料下载
链接: 百度网盘 请输入提取码 提取码: tifs
链接: https://pan.baidu.com/s/1RxtQqriOzeggsJntKs9TIg?pwd=tifs 提取码: tifs
一、问题分析
问题1分析:数据变换与误差分析
问题1的目标是根据附件1中的数据
,建立一个数学模型,通过某种变换使得变换后的数据结果尽可能接近原始数据。首先,我们需要选择合适的变换方法,例如线性变换、非线性变换或其他数学操作(如归一化、标准化等),以确保变换后的数据与原数据保持高度一致。变换后的数据和原数据之间的误差是评估变换效果的关键。常用的误差度量包括均方误差(MSE)和平均绝对误差(MAE)。此外,问题中还要求分析误差来源,特别是数据噪声和模型偏差对结果的影响。噪声可能来自测量误差或外部环境的干扰,而模型偏差则可能是由于所选变换方法不完全适应数据结构所致。因此,分析误差的来源并提出改进方案,对于提高模型精度具有重要意义。
问题2分析:数据压缩与还原模型
问题2要求我们建立一个数据压缩模型,将附件2中的矿山监测数据进行降维处理,并计算压缩效率。降维的目的是减少数据的维度,同时保留尽可能多的原始信息。我们可以使用常见的降维方法,如主成分分析(PCA)、独立成分分析(ICA)等。降维后的数据可以显著减少存储空间需求和计算复杂度。压缩效率的衡量标准包括压缩比(降维后数据的维度与原数据维度的比值)和存储空间节省率(降维后的存储需求相对于原数据存储需求的减少比例)。进一步,我们需要建立数据还原模型,将降维后的数据还原到原始空间,并分析还原对数据质量的影响。还原数据的准确度可以通过均方误差(MSE)来衡量,我们的目标是确保MSE不超过0.005。在保证数据还原准确度的同时,我们还需要尽可能提高压缩效率,以达到更好的存储和计算优化效果。
问题3分析:去噪与标准化处理
问题3涉及到矿山监测数据中的噪声影响。数据X可能包含由于测量误差或外部环境变化引入的噪声,因此需要进行去噪和标准化处理。数据去噪通常可以通过滤波、平滑等方法实现,如小波去噪或移动平均等。去噪后的数据能够更加真实地反映原始信号,从而提高后续建模的准确性。标准化处理则是为了消除不同特征之间量纲不一致的问题,确保每个特征在相同的尺度下进行建模。标准化后的数据均值为0,方差为1,使得不同的特征不会对模型产生不均衡的影响。在去噪和标准化处理之后,我们需要建立X与Y之间的关系模型,计算拟合优度并进行统计检验,确保模型具有较强的解释能力。评估拟合优度的指标包括和均方误差(MSE),并且需要验证模型的稳定性和解释能力,以确保模型在不同情况下均能有效应用。
问题4分析:自适应调整与模型拟合
问题4要求建立数据
与目标变量之间的关系模型,并设计一个自适应调整算法,以确保模型拟合优度尽可能高。自适应调整算法的核心任务是自动优化模型的超参数,从而提高模型的预测性能。常见的自适应调整方法包括网格搜索、随机搜索和贝叶斯优化等,它们通过不断调整超参数,帮助模型找到最佳配置,从而最大化拟合优度。拟合优度通常通过
值来衡量,值越高,说明模型的拟合效果越好。同时,我们还需要计算模型的平均预测误差,常用的误差度量是均方误差(MSE),它衡量模型在测试集上的预测精度。此外,问题还要求评估模型的稳定性和适用性,确保模型在不同数据集上的表现一致,具备较强的泛化能力。通过交叉验证等方法,我们可以验证模型在不同情况下的稳定性。
问题5分析:高维数据降维与重构
问题5的任务是对高维数据进行降维处理,并建立降维数据到原始数据空间的重构模型。降维的目标是从原始的高维数据中提取出最有意义的低维表示,从而提高数据处理的效率。降维方法包括PCA、t-SNE和自编码器等。降维后的数据能够有效减少计算复杂度,但可能会丢失部分细节。为了确保数据的可解释性,我们需要建立一个重构模型,通过降维后的数据恢复出原始数据的主要特征。重构模型的准确性可以通过计算重构误差来评估,常用的误差度量是均方误差(MSE)。在建立重构模型的同时,我们还需要保证降维数据与目标变量之间的关系模型的准确性和有效性。最终,我们需要评估模型的效果,包括其泛化能力和算法的复杂度,确保在保证重构精度的同时,能够提高计算效率并适应大规模数据处理。
2025五一数学建模B题助攻资料下载
链接: 百度网盘 请输入提取码 提取码: tifs
2025五一数学建模B题助攻资料下载
链接: 百度网盘 请输入提取码 提取码: tifs
链接: https://pan.baidu.com/s/1RxtQqriOzeggsJntKs9TIg?pwd=tifs 提取码: tifs
二、问题重述
问题1:数据变换与误差分析
问题1的目标是通过对附件1中的数据
进行某种变换,使得变换后的结果尽可能接近原始数据
。在这个过程中,我们需要建立一个数学模型,选择适合的变换方法,并对变换后的数据进行评估。关键的评估标准是计算变换后的结果与原始数据之间的误差,常用的误差度量包括均方误差(MSE)。此外,我们还需要分析误差的来源,可能的原因包括数据噪声、模型偏差或变换方法不适应数据特性等因素。通过识别这些误差来源,我们能够提出改进措施,优化变换过程,确保得到尽可能准确的结果。
问题2:数据压缩与还原模型
问题2要求我们对附件2中的矿山监测数据进行降维处理,并建立数据压缩模型。降维处理的目的是减少数据的维度,减轻计算和存储负担,同时尽可能保留数据的关键信息。我们需要计算压缩效率,包括压缩比和存储空间节省率,衡量降维效果。同时,问题要求我们建立数据还原模型,将降维后的数据还原回原始空间,并分析降维和还原对数据质量的影响。我们需要确保在保证还原数据准确度的前提下,尽量提高压缩效率,且还原后的数据的均方误差(MSE)不能高于0.005。
问题3:数据去噪与标准化处理
问题3聚焦于矿山监测数据分析中的噪声问题,要求对附件3中的两组矿山监测数据进行去噪和标准化处理。数据去噪的目标是减少或去除由于测量误差、外部环境干扰等因素引入的噪声,使得数据更加清晰和准确。标准化处理是将数据的不同特征统一到相同的尺度上,以消除特征间的尺度差异。完成去噪和标准化处理后,我们需要建立数据与目标变量之间的关系模型,并计算模型的拟合优度。拟合优度的评估将通过值和均方误差(MSE)等指标来进行,此外还需要进行统计检验,确保模型在解释与之间关系时具有较强的稳定性和解释能力。
问题4:自适应调整与模型拟合
问题4要求我们建立数据与目标变量之间的关系模型,并设计一个自适应调整算法,以最大化模型的拟合优度。自适应调整算法的核心目标是优化模型的超参数,从而提高模型的预测能力。我们需要选择适当的回归模型(如线性回归、支持向量回归等),并通过自适应算法(如网格搜索、随机搜索或贝叶斯优化等)调整模型的超参数,使得模型拟合优度尽可能高。在此过程中,我们还需要计算模型的平均预测误差,评估模型的稳定性,并确保模型能够适应不同数据集的变化,具备较强的泛化能力
问题5:高维数据降维与重构
问题5的目标是对矿山监测的高维数据进行降维处理,并建立降维数据到原始数据空间的重构模型。降维处理的目的是将数据从高维空间压缩到低维空间,以减少计算复杂度和存储需求,同时保留数据的主要特征。降维后的数据需要通过重构模型还原回原始空间,以确保数据的可解释性和信息完整性。我们需要探讨降维与重构之间的平衡关系,即如何在降低数据维度的同时,尽量减少重构误差,确保数据在降维后的表示能够有效预测目标变量
。最终,我们还需要评估所建立模型的效果,包括模型的泛化能力和算法的计算复杂度等。
2025五一数学建模B题助攻资料下载
链接: https://pan.baidu.com/s/1RxtQqriOzeggsJntKs9TIg?pwd=tifs 提取码: tifs
2025五一数学建模B题助攻资料下载
链接: 百度网盘 请输入提取码 提取码: tifs