当前位置： 首页 > news >正文

AVL搜索树

news 来源：原创 2025/5/23 3:26:42

目录

一、AVL树的概念

二、AVL树的定义

三、旋转

四、测试

一、AVL树的概念

二叉搜索树虽然可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化成单支树，查找元素相当于在顺序表中搜索元素，效率低下。因此就有了AVL树：当向二叉搜索树中插入新节点后，如果能保证左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即课降低树的高度，从而减少平均搜索长度。

一颗AVL树或者是空树，或者是具有以下性质的二叉搜索树:
它的左右子树都是AVL树

左右子树的高度之差（简称平衡因子)的绝对值不超过1

那为什么是左右高度差不超过1呢

 如果是偶数就做不到完全是0的情况，也就是在某些数量情况下，做不到相等

二、AVL树的定义

template<class K,class V>
struct AVLTreenode
{
	AVLTreenode<K,V>* _left;
	AVLTreenode<K, V>* _right;
	AVLTreenode<K, V>* _parent;
	pair<K,V> _kv;
	int _bf;//平衡因子
	AVLTreenode(const pair<K, V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_kv(kv)
		,_bf(0)
	{

	}
};
template<class K, class V>
class AVLTree
{
	typedef AVLTreenode<K, V> Node;
public:

private:
	Node* _root = nullptr;
};

2.1插入

比如说插入在8的左边会导致8的平衡因子更新成0，但是8的父亲是不受影响的

新增节点是可能影响祖先的(子树的高度是否变化)

1.子树的高度不变，就不会继续往上影响祖先

2.反之则会

插入节点如果在9的右边的话，就会影响到8了，至于为什么不在继续往上更新了呢，因为此时这个棵树都不是AVL树了，我们要进行调整

总结 

新增节点在左子树，父亲bf--；

新增节点在右子树，父亲bf++

更新后：

1.父亲的bf更新后==0，父亲所在的子树高度不变，不用再继续往上更新，插入结束了

注：在插入节点之前，父亲bf==1或-1，一边高一边低，新插入节点填上低的那边

2.父亲的bf更新后==1or-1，父亲所在的子树高度变了，不继续往上更新

注：在插入节点之前，父亲==0两边一样高，插入导致高度变化了

3.父亲的 bf更新后==2or-2，此时已经不是AVL树了，违反规则，必须调整处理 

那我们开始处理这个平衡因子 首先我们来判断结束条件，结束条件是由一种情况能看出来的

这样子会一直更新到parent的，所以我们的结束条件也可以判断了

三、旋转

其次我们来处理这个旋转，就是平衡因子为2或者是-2的时候所导致的调整

比如说这种情况

首先旋转我们要注意两个条件

1.左右均衡一些

2.保持搜索树的规则 

我们需要一个压的住两边的父亲，才更新平衡因子 

这是一种比较简单的情况，接下来我们来看一种比较复杂的情况

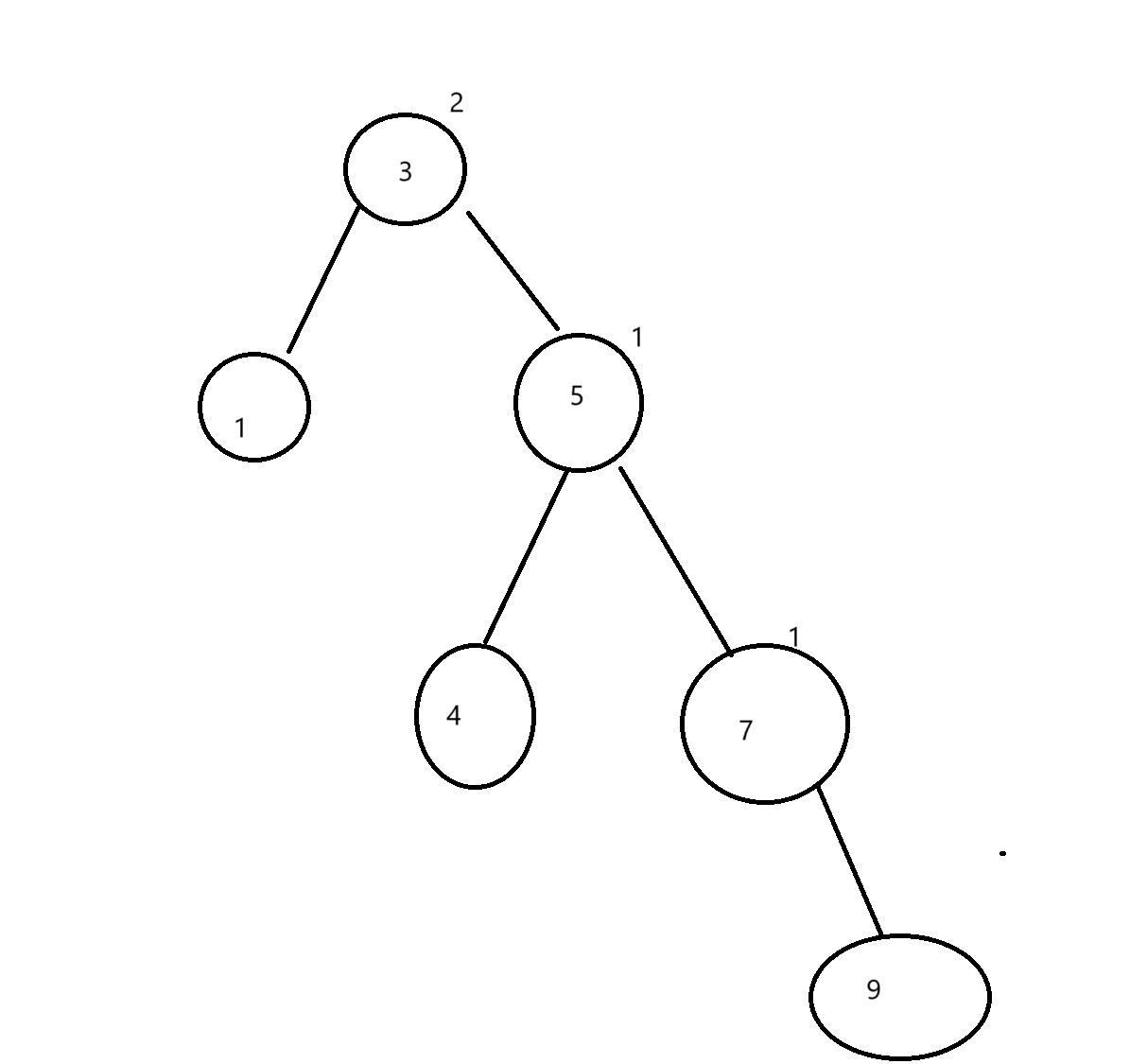
 我们想3的平衡因子太高了所以我们要把它压下来，压下来我们要找一个压的住的，所以我们选5来做这个，但是5的左边也有一个孩子，我们可以把它往3的右边放(因为它在3的右子树肯定比3大)

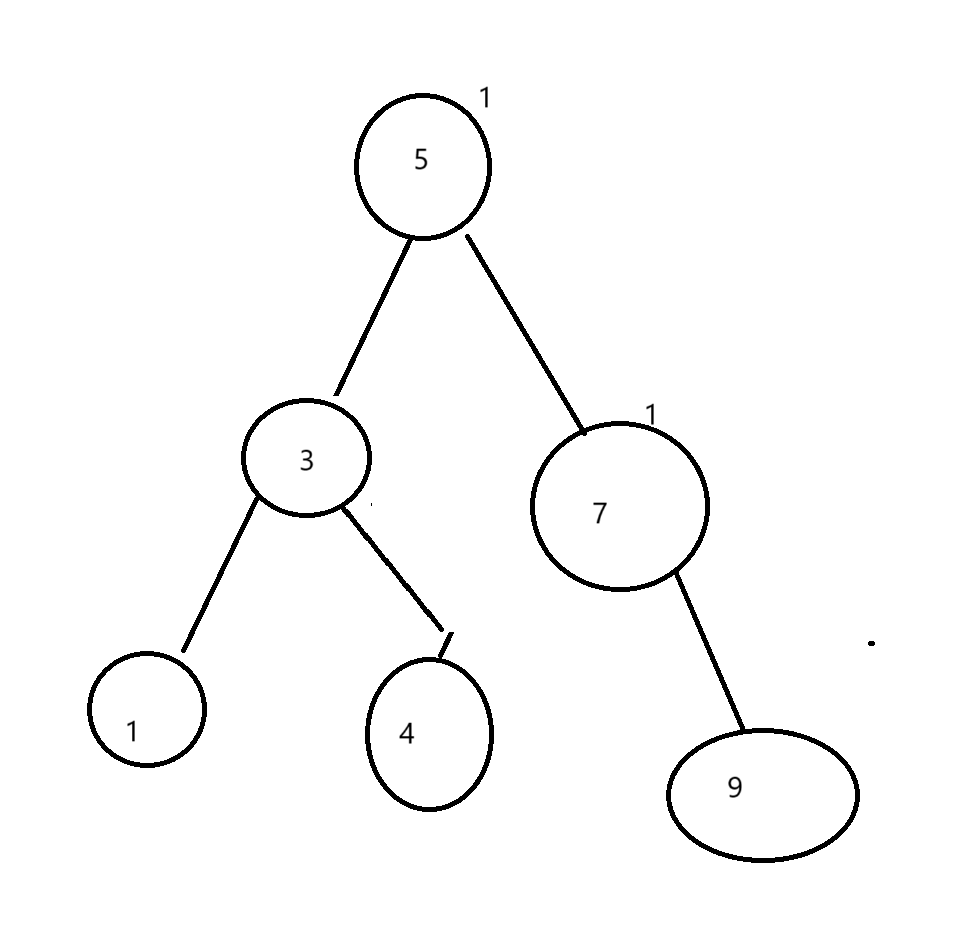
这是左单旋的例子，既然有例子，就有概念 

3.1新节点插入较高右子树的右侧-左单旋

 

 

我们着重讲一下2的这一种，a b是x，y，z中任意一种， c必须是x

如果c是y或者z，c的位置要新增，c的位置要不违反avl树，才能继续往上更新，那我们在y的右或者在z的左插入，c是不会向上更新的，在y的左或者z的右插入呢，c就不是avl树了，也不会向上更新，但是我们最终的目的是让10，20变为左单旋，这是不符合的

如果我们把h==2的所有场景穷举出来，就是3*3九种组合

插入位置有4个位置

合计36种情况

但是我们不关注下面的情况，我们只关注10，20那个节点，也就是平衡因子为2的节点我们要把它压下来进行左单旋

	void RoLeft(Node* parent)
	{
		Node* SubR = parent->_right;
		Node* SubRL = SubR->_left;

		parent->_right = SubRL;
		SubR->_left = parent;
		if(SubRL)
		SubRL->_parent = parent;

		Node* parentParent = parent->_parent;
		parent->_parent = SubR;
		if (_root == parent)
		{
			_root = SubR;
			SubR->_parent = nullptr;
		}
		else {
		  if (parentParent->_left==parent)
		  {
			parentParent->_left = SubR;
	     	}
		  else 
		  {
			parentParent->_right = SubR;
		   }
	     	SubR->_parent = parentParent;
		}
		parent->_bf = SubR->_bf = 0;
	}

3.2右单旋

	void RoRight(Node* parent)
	{
		Node* SubL = parent->_left;
		Node* SubLR = SubL->_right;
		SubL->_right = parent;
		parent->_left = SubLR;
		if (SubLR)
			SubLR->_parent = parent;
		Node* parentParent = parent->_parent;
		parent->_parent = SubL;
		if (_root == parent)
		{
			_root = SubL;
			SubL->_parent = nullptr;
		}
		else
		{
			if (parentParent->_left==parent)
			{
				parentParent->_left = SubL;
			}
			else
			{
				parentParent->_right = SubL;
			}
			SubL->_parent = parentParent;
		}
		parent->_bf=SubL->_bf=0;
	}

 那如果我们是在左单旋的左侧位置进行插入呢

3.3右左双旋

这个时候大家可以去画一下图，简单的左单旋已经解决不了这里的问题了 

这时候还要再把b再拆解一下才能解决问题

a和d是高度为h的avl树(h>=0)

b和c是高度为h-1的avl树或者是空树 (h>=1)

这里30就是新增

 

在30的左边或者是右边新增

 h==2也是和左单旋类似一样的道理

总而言之我们可以分为两种情况

一种是h==0，30就是新增

一种是h>=1，在b或者c就是新增

那这两种主要是在平衡因子上的差别

方法：1.40为旋转点进行右单旋

2.20为旋转点进行左单旋

我们先处理局部，30的左边不是高吗我们先处理30的左边，这样就变成了纯粹的右边高

我们再进行一个对20左单旋就可以了 

那我们旋转完成的平衡因子该如何更新 ，这里我们动的是30，20，40因为它们的孩子都动了

双旋在这里是把30推成这棵树的根 ，把30的左边b分给了20的右边(右单旋),把30的右边c分给了40的左边(左单旋)，让b，c在30的左右两边

那在c插入也是更上面一样的道理，这里我就不画图了，写一个平衡因子贴在这里，20 -1，30 0，40 0

我们再来画一下h==0的这种情况

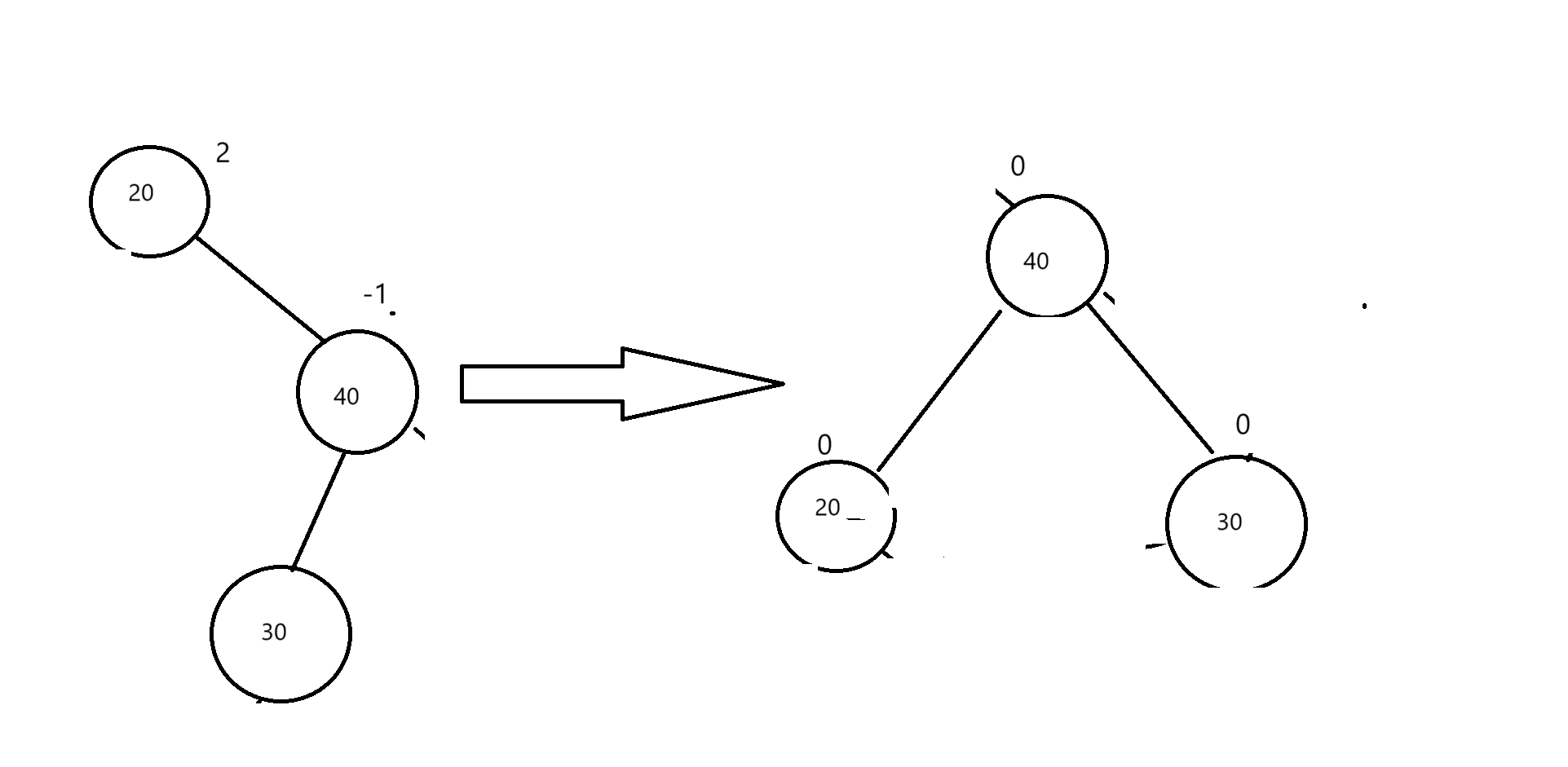
我们可以发现这三种情况的平衡因子都是有区别的都需要我们做讨论 

那我们根据什么来区别呢，这里是根据30的平衡因子来区分的，在b插入，30的平衡因子就是-1，

c插入，30的平衡因子就是1，30自己就是新增，平衡因子就是0

那我们先来写一下右左双旋

	void RoRL(Node* parent)
	{
		Node* SubR = parent->_right;
		Node* SubRL =SubR->_left;
		int bf = SubRL->_bf;//因为会不停的变
		RoRight(SubR);
		RoLeft(parent);
		if (bf == 0)
		{
			parent->_bf = SubR->_bf = SubRL->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			SubR->_bf = 1;
			SubRL = 0;
		}
		else if (bf == 1)
		{
			parent->_bf =-1;
			SubR->_bf = 0;
			SubRL = 0;
		}
		else
		{
			assert(false);
		}
	}

3.4左右双旋

	void RoLR(Node* parent)
	{
		Node* SubL = parent->_left;
		Node* SubLR = SubL->_right;
		int bf = SubLR->_bf;
		RoLeft(SubL);
		RoRight(parent);
		if (bf == 0)
		{
			parent->_bf = SubL->_bf = SubLR->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = 0;
			SubL->_bf =-1;
			SubLR = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			SubL->_bf = 0;
			SubLR = 0;
		}
		else
		{
			assert(false);
		}
	}
bool Insert(const pair<K,V>& kv)
{
	if (_root == nullptr)
	{
		_root = new Node(kv);
		return true;
	}
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (cur->_kv.first < kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_kv.first > kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}
      cur = new Node(kv);
	if (parent->_kv.first< kv.first)
	{
		parent->_right = cur;
		cur->_parent=parent;
	}
	else
	{
		parent->_left = cur;
		cur->_parent = parent;
	}
	//旋转
	while (parent)
	{
		if (cur==parent->_left)
		{
			parent->_bf--;
		 }
		else
		{
			parent->_bf++;
		}
		if (parent->_bf == 0)
		{
			break;
		}
		else if (parent->_bf == 1 || parent->_bf == -1)
		{
			cur = parent;
			parent = parent->_parent;
		}
		else if(parent->_bf == 2 || parent->_bf == -2)
		{
			//旋转
			if (parent->_bf == 2 && cur->_bf == 1)
			{
				RoLeft(parent);
			}
			else if(parent->_bf == 2 && cur->_bf == -1)
			{
				RoRL(parent);
			}
			else if(parent->_bf == -2 && cur->_bf == -1)
			{
				RoRight(parent);
			}
			else if (parent->_bf == -2 && cur->_bf == 1)
			{
				RoLR(parent);
			}
			break;
		}
	     else
	    {
		 assert(false);
	    }
	}

	return true;
}

1.旋转让这颗子树平衡了

2.旋转降低了这颗子树的高度，恢复到跟插入以前一样的高度，所以对上一层没有影响，不用更新

	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

    void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;

		_InOrder(root->_left);
		cout << root->_kv.first << " ";
		_InOrder(root->_right);
	}
四、测试
int main()
{
	int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	AVLTree<int, int> t;
	for (auto e : a)
	{
		t.Insert(make_pair(e, e));
	}
	t.InOrder();

	return 0;
}

 

这个我们只能确定它是搜索树，那怎么判断它是平衡树

2.3判断平衡

	bool IsBalance()
	{
		return _IsBalance(_root);
	}
	int _Height(Node* root)
	{
		if (root == nullptr)
		{
			return 0;
		}
		int leftheight= _Height(root->_left);
		int rightheight = _Height(root->_right);
		return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
	}

	bool _IsBalance(Node* root)
	{
		if (root == nullptr)
			return false;
		int leftheight = _Height(root->_left);
		int rightheight = _Height(root->_right);
		if (rightheight - leftheight != root->_bf)
		{
			cout << root << "->" << "平衡因子异常" << endl;
		}
		return abs(leftheight - rightheight) < 2;
	}

判断平衡因子要注意遵守左右子树高度差不超过1 

int main()
{
	const int N = 20;
	vector<int> v;
	v.reserve(N);
	srand(time(0));

	for (size_t i = 0; i < N; i++)
	{
		v.push_back(rand());
		cout << v.back() << endl;
	}

	AVLTree<int, int> t;
	for (auto e : v)
	{
		t.Insert(make_pair(e, e));
		cout << "Insert:" << e << "->" << t.IsBalance() << endl;
	}

	cout << t.IsBalance() << endl;

	return 0;
}

这里是测试代码

 AVL树其实不是很难，但是细节的地方考验的很多，稍微一个不注意就可能引发一连串的报错，所以我们写这类代码的时候很考验我们的耐心，接下来进入红黑树

相关文章：

  • 互斥锁(mutex) ---- 静态锁与动态锁
  • （C语言）算法复习总结1——二分查找
  • 【T2I】Region-Aware Text-to-Image Generation via Hard Binding and Soft Refinement
  • GPT-2 语言模型 - 模型训练
  • 关于柔性数组
  • 开源项目faster-whisper和whisper是啥关系
  • C语言之continue相关题目
  • 剖析 Rust 与 C++：性能、安全及实践对比
  • 【频域分析】对数谱
  • app逆向专题四：charles抓包工具配置
  • Relief法**是一种非常经典、有效的**特征选择算法
  • Java—— 文字版格斗游戏
  • 整型与布尔型的转换
  • 二分三分算法详解, 模板与临界条件分析
  • Android开发：应用DeepSeek官方Api在App中实现对话功能
  • 智能制造方案精读：117页MES制造执行系统解决方案【附全文阅读】
  • vue webSocket
  • 腾势品牌欧洲市场冲锋，科技豪华席卷米兰
  • CSI-PVController-claimWorker
  • 【Unity精品源码】Ultimate Character Controller：高级角色控制器完整解决方案
  • 数据库怎么做两个网站/长沙弧度seo
  • 青海建设银行的官方网站/优化网站关键词
  • 深圳做网站比较好的公司有哪些/免费创建网站软件
  • 网站开发应该先写前端还是后端/谷歌网址
  • 建设人才库网站/广州市新闻最新消息
  • 网站运行维护/昆明seo案例