【挠头写算法系列】质疑分治,理解分治,到分治真香
前言
断更了好久的算法,原因是之前进度太慢,要是加上写博客更慢了,现在今天就继续更新后续的一些算法。
首先今天要讲的就是”分治“,什么是分治呢,这里就不把一长串的概念给大家复制出来了,我直接用通俗,直观的方式告诉大家,常见的分治就是我们之前听说过的“快速排序”,与”归并排序“。如果还是不太理解,没事,下面的文章我会更加详细的讲解什么是分治。但在这之前我们就需要先回顾快速排序,与归并排序。
快速排序
之前我在数据结构专栏讲过快速排序,而且还讲了许多优化方法,现在我们只讲朴素的快速排序,来理解分治
在快速排序中,我们就是不断重复一个操作,就是先选定一个区间中的任意一个元素key,然后将这段区间变成
左边小于key,右边大于key,这样就是一次操作,然后我们继续对这左右两边进行再次这样的操作,直到这自己选定的区间只有一个元素,这样我们就将一个数组排序完成了。
import java.util.Random;
class Solution {
public int[] sortArray(int[] nums) {
func(nums,0,nums.length-1);
return nums;
}
public void func(int[] nums,int l,int r){
if(l>=r) return;
int n=nums[new Random().nextInt((r-l+1))+l];
int left=l-1,right=r+1,i=l;
while(i<right){
if(nums[i]<n) swap(nums,i++,++left);
else if(nums[i]==n) i++;
else swap(nums,i,--right);
}
func(nums,l,left);
func(nums,right,r);
}
public void swap(int[] nums,int i,int j){
int t=nums[i];
nums[i]=nums[j];
nums[j]=t;
}
}归并排序
与快速排序既相似也可以说相反,因为归并排序是不断将一段区间进行对半分,直到这段区间长度为1,我们就可以返回去合并两段区间进行排序(此时合并的是两段已经有序的区间),是一种递归过程把,可以类似这样看:快速排序更像是一种前序遍历,在对半分之前,已经将这段区间变成左右两边性质不同的,即(大于key和小于key)。而我们的后续遍历就是无脑的将区间进行对半分,直至不能再分,才开始回退到前一次分割之前进行排序,直至回退到开始分割的时候,数组也就排序好了。
class Solution {
public int[] sortArray(int[] nums) {
func(nums,0,nums.length-1);
return nums;
}
public void func(int[] nums,int l,int r){
if(l>=r) return;
int mid=(l+r)/2;
func(nums,l,mid);
func(nums,mid+1,r);
func1(nums,l,r,mid);
}
public void func1(int[] nums,int l,int r,int mid){
int i=l,j=mid+1,k=0;
int[] arr= new int[r-l+1];
while(i<=mid&&j<=r){
if(nums[i]<=nums[j]) arr[k++]=nums[i++];
else arr[k++]=nums[j++];
}
while(i<=mid){
arr[k++]=nums[i++];
}
while(j<=r){
arr[k++]=nums[j++];
}
for(i=0;i<r-l+1;i++){
nums[l+i]=arr[i];
}
}
public void swap(int[] nums,int i,int j){
int t=nums[i];
nums[i]=nums[j];
nums[j]=t;
}
}分治真正的运用
难道分治就是仅仅只是用来排序的吗,当然不是。接下来我们就通过几个题目,真正了解分治的真正奥妙。
第k大

如上题目,很简单的一题,相信很多人都想到运用堆去解决这个问题,但其实这题,也可以运用我们的快速排序去解决,而且时间复杂度更优,也就是题目中所说的O(n)的时间复杂度。
首先我们要直到在快速排序中,其实我们已经对一段区间的元素进行大致的划分,而且题目中不是要求我们排序,而是找到第k个最大元素,我们将这段区间划分成 <key ==key >key 这三段区间,那么我们只需先看看这三段区间中哪个区间可能包含有那个第k大
我们将这三段区间的数量个数进行统计为 a b c
如果k<c,那么说明第k大就是在 >key区间找即可,就无需在理会剩下两个区间,
如果不是上面那种情况我们并且 b+c>k, 这就说明我们要找到的第k大就是在b这段区间内,因为跳过了上面那种情况说明不在区间c中,那么只能在区间b中,所以他就是key
如果上面两种情况都不在,那肯定是在区间a中,那么我们只需要在区间a中找第k-(b+c)大即可。
class Solution {
public int findKthLargest(int[] nums, int k) {
return pation(nums,0,nums.length-1,k);
}
public int pation(int[] nums,int l,int r,int k){
if(l>=r) return nums[l];
int left=l-1,right=r+1,i=l;
int key=nums[(r+l)/2];
while(i<right){
if(nums[i]<key) swap(nums,i++,++left);
else if(nums[i]==key) i++;
else swap(nums,i,--right);
}
if((r-right+1)>=k) return pation(nums,right,r,k);
else if(k<=(r-left)) return key;
else return pation(nums,l,left,k-r+left);
}
public void swap(int[] nums,int i,int j){
int t=nums[i];
nums[i]=nums[j];
nums[j]=t;
}
}逆序对

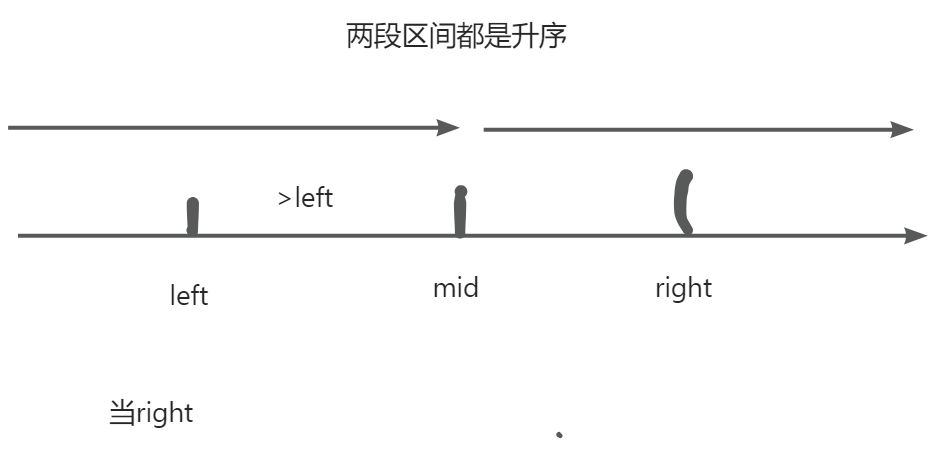
在归并排序合中向上返回并两个区间时,这两个区间就已经是拍好序得了,假设两个区间都是升序
那么在合并过程中,如果我们能找到右边区间的某个元素right小于左边某个元素left,那么就可以确定,
在left-mid的元素也都比right大,这不就刚好算出有mid-right+1,逆序对了吗,这就时归并排序的奥妙之处,能在合并排序过程中一边利用排序好的性质一边对逆序对进行运算。
class Solution {
public int reversePairs(int[] record) {
return mer(record,0,record.length-1);
}
public int mer(int[] nums,int l,int r){
if(l>=r) return 0;
int ret=0;
int mid=(l+r)/2;
ret+=mer(nums,l,mid);
ret+=mer(nums,mid+1,r);
int[] tmp=new int[r-l+1];
int cur1=l,cur2=mid+1,i=0;
while(cur1<=mid&&cur2<=r){
if(nums[cur1]<=nums[cur2]) tmp[i++]=nums[cur1++];
else{
tmp[i++]=nums[cur2++];
ret+=mid-cur1+1;
}
}
while(cur1<=mid) tmp[i++]=nums[cur1++];
while(cur2<=r) tmp[i++]=nums[cur2++];
for(int j=0;j<(r-l+1);j++) nums[l+j]=tmp[j];
return ret;
}
}