当前位置：首页 > news >正文

运动规划实战案例 | 基于可视图的路径规划算法(附ROS C++/Python仿真)

news 来源：原创 2025/6/21 4:06:00

1 拓扑图路径规划

在传统栅格或采样方法中，算法需要在密集的高维数据中逐点搜索，计算量随环境规模指数级增长。拓扑图路径规划算法的核心思想在于将复杂的高维连续空间抽象为低维的离散图结构，通过提取环境中的关键拓扑特征（如房间、走廊、路口等）作为节点，并将这些特征之间的连通关系抽象为边，从而构建出反映空间连通性的简化网络模型。这种降维策略通过忽略环境中的几何细节与冗余信息，将路径搜索问题从原始的连续坐标空间映射到离散的拓扑图空间，使算法只需在稀疏的图结构中寻找节点间的最短连通路径，大幅降低了规划问题的复杂度。

在这里插入图片描述

此外，拓扑图天然刻画了环境的层次化连通关系，能够识别出全局最优路径必经的枢纽节点，避免陷入局部最优陷阱。总结而言，拓扑图在保持路径可行性的前提下，以计算效率换取了环境建模的精度，为大规模复杂场景下的实时路径规划提供了轻量化解决方案。

2 可视图算法原理

可视图(Visibility Graph)是由运动环境中障碍物抽象而成的多边形顶点构建的可通行路网。

如图所示，首先将起点、终点与所有障碍物的顶点共同作为图节点，然后遍历所有节点对并检测它们之间的视线是否被障碍物阻挡，若两点间的直线路径不与任何障碍物相交则建立连接边，最终形成一个包含所有可行直线路径的可见性图。接着，通过Dijkstra等经典图搜索算法即可求解从起点到终点的拓扑最短路径

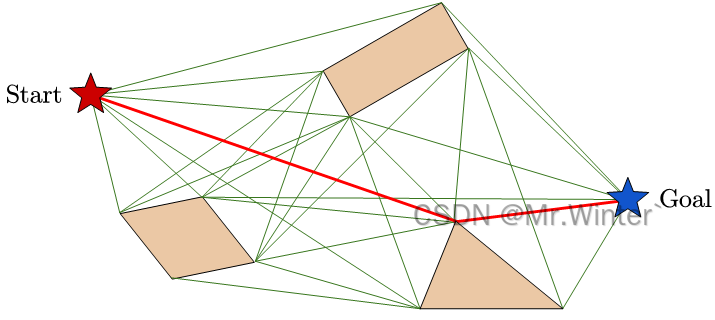
在这里插入图片描述

3 可视图构建案例

接下来用图例说明可视图的生成过程。

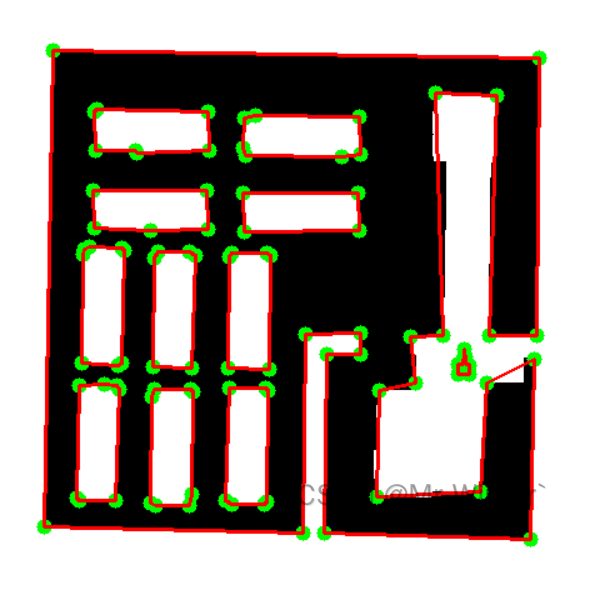
障碍物膨胀处理

根据机器人半径或安全间距，将原始障碍物边界向外扩展(白色的是障碍物，黑色的是自由空间)

在这里插入图片描述

关键顶点提取

提取膨胀后障碍物多边形所有顶点，添加起点 $S$ 、终点 $G$ 为特殊顶点，形成顶点集合 $V=\{v_1,v_2,...,v_n,S,G\}$

在这里插入图片描述

可见性检测
遍历所有顶点对 $v_i,v_j)$ ，检查连线 $v_iv_j$ 是否穿过障碍物，将没穿过的安全连线 $v_iv_j$ 添加到边集合 $E$ ，边权重取顶点间欧氏距离，生成带权无向图 $G (V, E)$ 。使用邻接表存储，对每个 $v_i$ 维护可见顶点列表
在邻接表上进行路径搜索

在这里插入图片描述

4 算法仿真

4.1 ROS C++实现

核心代码如下所示：

bool VisibilityPathPlanner::_searchOnRoadMap(const RoadMap& road_map, int start_idx, int goal_idx,
                                             std::vector<int>& path)
{
  const double INF = std::numeric_limits<double>::infinity();
  int node_count = static_cast<int>(road_map.size());
  std::vector<double> dist(node_count, INF);
  std::vector<int> prev(node_count, -1);
  using QueueNode = std::pair<double, int>;
  std::priority_queue<QueueNode, std::vector<QueueNode>, std::greater<>> OPEN;
  dist[start_idx] = 0;
  OPEN.emplace(0.0, start_idx);

  // dijkstra loop
  while (!OPEN.empty())
  {
    auto node = OPEN.top();
    double curr_dist = node.first;
    int u = node.second;
    OPEN.pop();

    // goal found
    if (u == goal_idx)
    {
      break;
    }

    if (curr_dist > dist[u])
    {
      continue;
    }

    // bfs
    for (const auto& road_node : road_map[u])
    {
      int v = road_node.first;
      double d = road_node.second;
      double new_cost = dist[u] + d;
      if (new_cost < dist[v])
      {
        dist[v] = new_cost;
        prev[v] = u;
        OPEN.emplace(new_cost, v);
      }
    }
  }

  // backtrace
  if (dist[goal_idx] == INF)
    return false;

  path.clear();
  for (int current = goal_idx; current != -1; current = prev[current])
  {
    path.push_back(current);
  }
  std::reverse(path.begin(), path.end());

  return true;
}

在这里插入图片描述

4.2 Python实现

核心代码如下所示：

def searchOnRoadMap(self, road_map: list, start_idx: int, goal_idx: int):
	"""
	Search the shortest path on road map using Dijkstra.
	
	Parameters:
	    road_map (list): road map connecting the start and goal
	    start_idx (int): the index of start point in road map
	    goal_idx (int): the index of goal point in road map
	
	Returns:
	    path (list): the planning path in indices
	    cost (float): the cost of planning path
	"""
	OPEN = []
	dist = np.full(len(road_map), np.inf)
	dist[start_idx] = 0
	prev = [-1] * len(road_map)
	heapq.heappush(OPEN, (0, start_idx))
	while OPEN:
	    curr_dist, u = heapq.heappop(OPEN)
	    if u == goal_idx:
	        break
	    if curr_dist > dist[u]:
	        continue
	    for v, d in road_map[u]:
	        if dist[v] > dist[u] + d:
	            dist[v] = dist[u] + d
	            prev[v] = u
	            heapq.heappush(OPEN, (dist[v], v))
	    
	if dist[goal_idx] == np.inf:
	    return None, np.inf
	
	path = []
	current = goal_idx
	while current != -1:
	    path.append(current)
	    current = prev[current]
	path.reverse()
	return path, dist[goal_idx]