代码训练营day22

回溯算法理论基础

回溯算法模板：

Void backtracking(参数) // 传入参数要根据代码逻辑来写

If (终止条件) {

       存放结果；

       返回

}

For (选择：本层集合中元素（树中节点的孩子数量是集合大小）) {

       处理节点；

       Backtracking（路径，选择列表）；

       回溯

}

解决问题：

1. 组合问题：

组合 1 2 3 4，在这个组合里找出大小为2的组合，12，13，14，23，24，34

1. 切割问题 给一个字符串，切割方式
2. 子集问题1 2 3 4 ，子集问题
3. 排列组合问题如果给一个组合12，他的排列方式有12和21两种
4. 棋盘问题

理解方式：抽象为树，集合大小确定树的宽度，递归深度确定树的深度

解题思路: 根据模板，考虑是在叶子处理问题，还是在每一个节点都要处理问题（子集）

77. 组合

题目链接/文章讲解：代码随想录  

视频讲解：带你学透回溯算法-组合问题（对应力扣题目：77.组合）| 回溯法精讲！_哔哩哔哩_bilibili

剪枝操作：带你学透回溯算法-组合问题的剪枝操作（对应力扣题目：77.组合）| 回溯法精讲！_哔哩哔哩_bilibili  

我自己尝试解了一下结果如下：

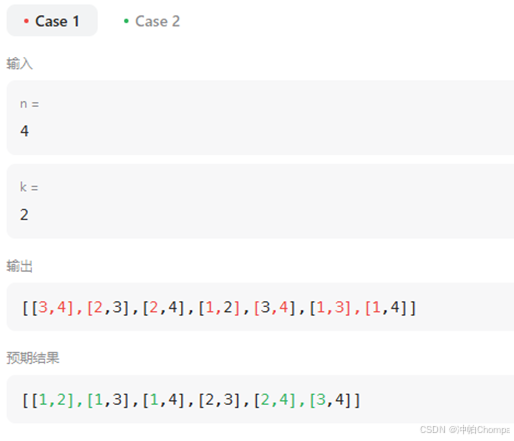
问题：

1. 先执行的递归逻辑所以输出顺序是从最后一个符合条件的组合开始的
2. 出现最后一个符合条件的组合重复是因为，每次他前面的数字都会顺序递归一次，

解决方法：更改终止条件

关于修剪枝叶，变量名和随想录中代码一致，设path.size()=2,n=7,k=5：

由K-path.size()=5-2=3,可知当前指针指位置后面至少还要有2个数字才能构成一个长度为k的组合，所以指针指向最多到当前位置，再继续遍历以及向下一层递归都是没有意义的，根据举的例子可知，7-3=4 说明1~4都可以取，指针至少可以取到4

考虑5，指针移动到5，将其加入组合，path.size()=3,还需要两个元素那就是下一次判断的过程了，说明5可以取，说明 指针每次至多移动7-（5-2）+1即：

n-(k-path.size())+1的位置 记为总长度减去还需要元素的数量再+1

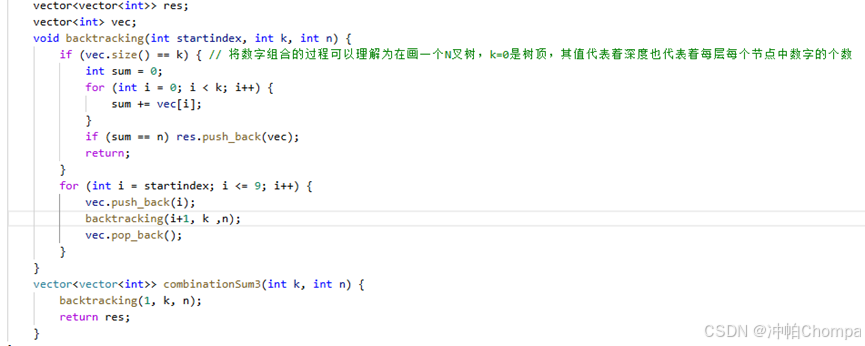
216.组合总和III

题目链接/文章讲解：代码随想录  

视频讲解：和组合问题有啥区别？回溯算法如何剪枝？| LeetCode：216.组合总和III_哔哩哔哩_bilibili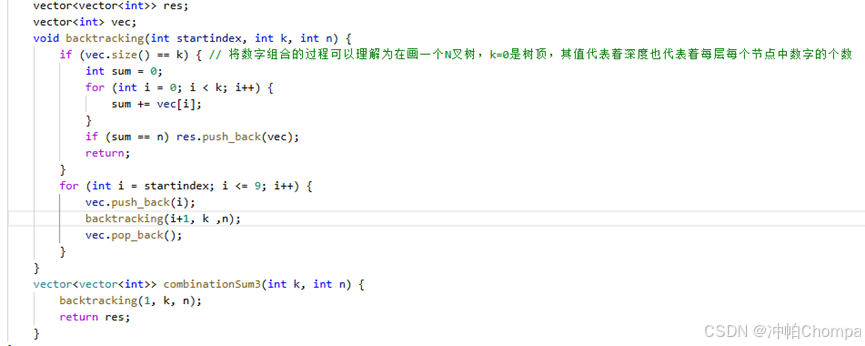

17.电话号码的字母组合

题目链接/文章讲解：代码随想录  

视频讲解：还得用回溯算法！| LeetCode：17.电话号码的字母组合_哔哩哔哩_bilibili

字母组合

字符串的长度：可进行组合字母的总数，以及组合的长度

组合中的每一个字母只来自于一个数字

解题思路：

1. 将数字映射成对应的字符串
2. 定义一个数组vec保存数字映射的字符串
3. 定义一个数组来存储结果
4. 定义一个字符串表示字母组合
5. 确定终止条件，字母组合的长度是等于原数字字符串的长度的，每一个字符只来源与一个数字对应的字符串，所以当组合的长度==原字符串的长度，更新结果
6. 单层的逻辑：一定要明白递归的下一层是下一个数字对应的字符串，所以需要一个索引startindex用来切换字符串。在本层中，要遍历当前字符串的所有元素
7. 单层的执行逻辑：首先将当前第一个字母加入str，然后开始递归找下一个字符串的一个字母（startidex+1），然后startindex-1且将当前尾字母移除（回溯），开始下一轮
8. 传入参数: vec, 原字符串长度，startindex
9. 且startindex不能大于原字符串长度，防止越界。