[Algorithm][动态规划][回文串问题][回文子串][最长回文子串][分割回文串Ⅳ]详细讲解
目录
- 0.原理讲解
- 1.回文子串
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 2.最长回文子串
- 1.题目链接
- 3.代码实现
- 3.分割回文串 IV
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
0.原理讲解
- 动态规划能够将所有的子串是否是回文的信息,保存在
dp表里面 - 状态表示一般经验:以
[i, j]为区间,分析问题
1.回文子串
1.题目链接
- 回文子串
2.算法原理详解
- 思路:
-
确定状态表示 ->
dp[i][j]的含义s字符串[i, j]的子串,是否是回文串
-
推导状态转移方程
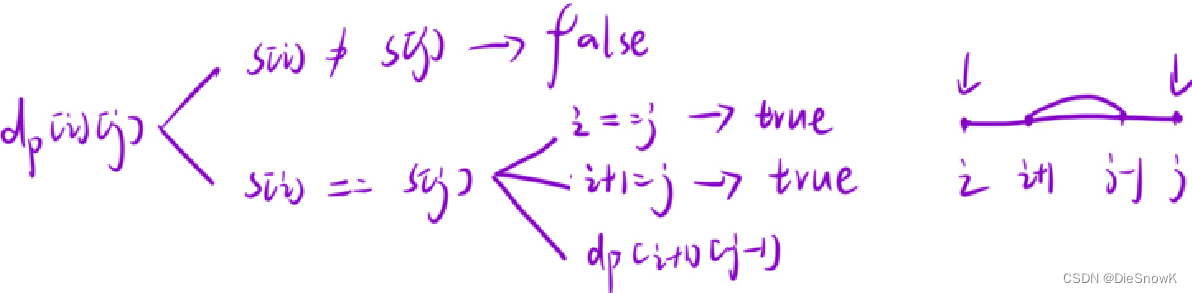
-
初始化:无需初始化
-
确定填表顺序:从下往上
-
确定返回值:
dp表里true的个数
-
3.代码实现
int countSubstrings(string s)
{
int n = s.size();
vector<vector<bool>> dp(n, vector<bool>(n));
int ret = 0;
for(int i = n - 1; i >= 0; i--)
{
for(int j = i; j < n; j++)
{
if(s[i] == s[j])
{
dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
if(dp[i][j])
{
ret++;
}
}
}
}
return ret;
}
2.最长回文子串
1.题目链接
-
最长回文子串
-
按照回文子串的思路解决即可,只不过判断最长时,利用起始下标
j - i + 1 -
思路:
-
确定状态表示 ->
dp[i][j]的含义s字符串[i, j]的子串,是否是回文串
-
推导状态转移方程
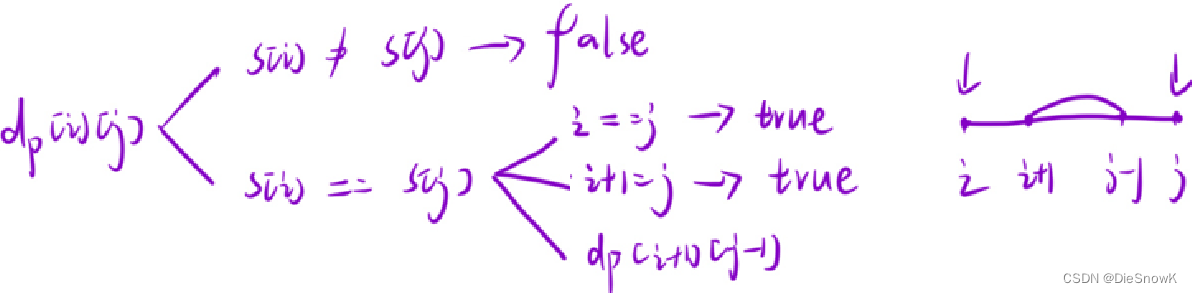
-
初始化:无需初始化
-
确定填表顺序:从下往上
-
确定返回值:
dp表里值为true的情况下,长度最大的字串的起始位置以及长度
-
3.代码实现
string longestPalindrome(string s)
{
int n = s.size();
vector<vector<bool>> dp(n, vector<bool>(n));
int len = 1, begin = 0;
for(int i = n - 1; i >= 0; i--)
{
for(int j = i; j < n; j++)
{
if(s[i] == s[j])
{
dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
if(dp[i][j] && j - i + 1 > len)
{
len = j - i + 1;
begin = i;
}
}
}
}
return s.substr(begin, len);
}
3.分割回文串 IV
1.题目链接
- 分割回文串 IV
2.算法原理详解
-
思路梳理:
- 本题思路经处理后,就可以划归为回文子串
- 可以将本题分为三个区间,其中中间区间就是一个回文子串的始末
- 先将字符串内所有子串是否是回文串都判断出来,再挨个判断三个区间是否是回文串
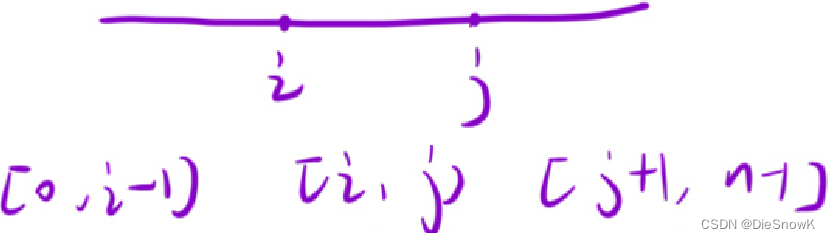
-
预处理:将字符串内所有子串是否是回文串都判断出来
-
确定状态表示 ->
dp[i][j]的含义s字符串[i, j]的子串,是否是回文串
-
推导状态转移方程

-
初始化:无需初始化
-
确定填表顺序:从下往上
-
-
结果处理:挨个判断三个区间是否是回文串
3.代码实现
bool checkPartitioning(string s)
{
// 预处理:处理回文信息
int n = s.size();
vector<vector<bool>> dp(n, vector<bool>(n));
for(int i = n - 1; i >= 0; i--)
{
for(int j = i; j < n; j++)
{
if(s[i] == s[j])
{
dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
}
}
}
// 判断三区间,枚举中间区间
for(int i = 1; i < n - 1; i++)
{
for(int j = i; j < n - 1; j++)
{
if(dp[0][i - 1] && dp[i][j] && dp[j + 1][n - 1])
{
return true;
}
}
}
return false;
}
