当前位置：首页 > wzjs >正文

做网站的花费网店推广营销方案

wzjs 2025/7/25 22:26:16

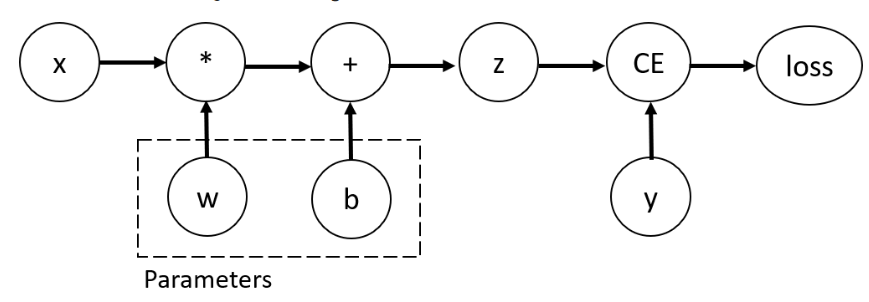
做网站的花费,网店推广营销方案,深圳做棋牌网站建设多少钱,专注手机网站建设1. autograd 对于一个很简单的例子，如下图所示，对于一个神经元z，接收数据x作为输入，经过激活函数，获得激活后的结果，最后利用损失函数获得损失，然后梯度反向回传。上图右侧即梯度反向回传的过…

1. autograd

对于一个很简单的例子，如下图所示，对于一个神经元z，接收数据x作为输入，经过 $\sigma$ 激活函数，获得激活后的结果，最后利用损失函数 $L$ 获得损失，然后梯度反向回传。

上图右侧即梯度反向回传的过程，其中字母上加一条线代表损失函数对该参数的偏导

损失函数L对自己的偏导为0
损失函数对y的偏导为 $\bar{y} = \bar{L}\cdot (y-t) = y-t$
损失函数对z的偏导为 $\bar{z} = \bar{y}\cdot {\sigma }'(z)$
损失函数对w的偏导为 $\bar{w} = \bar{z}\cdot x$
损失函数对b的偏导为 $\bar{b} = \bar{z}\cdot 1 = \bar{z}$

在实际使用中我们会将复杂的操作分解成若干个简单操作：

1.1 标量梯度反向回传

以下是pytorch官网的一个小示例：

import torch

x = torch.ones(5) # input tensor
y = torch.zeros(3) # expected output
w = torch.randn(5, 3, requires_grad=True)
b = torch.randn(3, requires_grad=True)
z = torch.matmul(x, w)+b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)

loss.backward() # 这里需要注意，只有标量才能直接调用，如果loss是一个张量的话需要在backward()中传入一个向量，且这个向量和loss的shape必须一样，一般而言向量元素全为1

print(w.grad)

print(b.grad)

1.2 张量梯度反向回传

inp = torch.eye(4, 5, requires_grad=True) # 创建一个对角矩阵，shape: [4, 5]
out = (inp+1).pow(2).t() # 矩阵元素加1，然后平方，再转置，shape: [5, 4]
out.backward(torch.ones_like(out), retain_graph=True) # 梯度反向回传，并且设置了保留梯度，可以多次调用，这个例子中out是一个shape: [5,4] 的张量，因此在backward中传入了一个shape:[5, 4] 的全1矩阵。
print(f"First call\n{inp.grad}")
out.backward(torch.ones_like(out), retain_graph=True) # 第二次调用，由于梯度未清零，因此会叠加
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_() # 梯度清零
out.backward(torch.ones_like(out), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")

First call
tensor([[4., 2., 2., 2., 2.],
        [2., 4., 2., 2., 2.],
        [2., 2., 4., 2., 2.],
        [2., 2., 2., 4., 2.]])

Second call
tensor([[8., 4., 4., 4., 4.],
        [4., 8., 4., 4., 4.],
        [4., 4., 8., 4., 4.],
        [4., 4., 4., 8., 4.]])

Call after zeroing gradients
tensor([[4., 2., 2., 2., 2.],
        [2., 4., 2., 2., 2.],
        [2., 2., 4., 2., 2.],
        [2., 2., 2., 4., 2.]])

2. 向量与张量的jarobian 矩阵计算

from torch.autograd.functional import jacobian
import torchdef func(x):return x.exp().sum(dim=1)x = torch.rand(2,3)
print(jacobian(func, x))

经过func之后的x由原来的shape: [2, 3] 变为了shape: [2]，而jacobian计算的过程是shape: [2]中的每个元素，对shape: [2, 3]中的每个元素求偏导，结果中为0的元素，代表func返回的结果中的第一个元素与x中第二行没关系，func返回的结果中的第二个元素与x中第一行没关系。

tensor([[[1.0939, 2.4570, 1.3270],
         [0.0000, 0.0000, 0.0000]],

        [[0.0000, 0.0000, 0.0000],
         [1.3719, 1.8973, 1.8708]]])

torch.manual_seed(5)
a = torch.randn(3)
print(a)
def func2(x):return a+x
x = torch.rand(3)
print(jacobian(func2, x))

tensor([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])

其他的示例懒得写了，代码放在这，有兴趣的可以自己看看，拷贝下来之后，把日志部分删掉或者改成print就可以跑了。

'''
1.讲解jarcobin矩阵
2.讲解向量和矩阵的梯度求解
'''
from torch.autograd.functional import jacobian
import torch
import loggerlogger1 = logger.logger_(__file__)def func(x):return x.exp().sum(dim=1)x1 = torch.rand(2,3, requires_grad=True)
print(jacobian(func, x1))'''经过func之后的x由原来的shape: [2, 3] 变为了shape: [2]，
而jacobian计算的过程是shape: [2]中的每个元素，对shape: [2, 3]中的每个元素求偏导，
结果中为0的元素，代表func返回的结果中的第一个元素与x中第二行没关系，
func返回的结果中的第二个元素与x中第一行没关系。'''
torch.manual_seed(5)
a = torch.randn(3)
print(a)
def func2(x):return a+x
x2 = torch.rand(3)
print(jacobian(func2, x2))#- 利用jacobian矩阵与某个全1的矩阵相乘，获得与反向回传相同的结果
def func(x):return x.exp().sum(dim=1)x1 = torch.rand(2,3, requires_grad=True)
print(jacobian(func, x1))y = func(x1)
y.backward(torch.ones_like(y))  # 这里为什么要加一个torch.ones_like(y)呢？
# 其实可以理解为Loss就是y，即loss = func(x1), Loss对Loss本身求偏导，那自然是全1，然后再对x求偏导，得到x' = loss'× func'(x1)
print(x1.grad)logger1.info(torch.ones_like(y) @ jacobian(func, x1))a = torch.randn(2, 3, requires_grad=True)
b = torch.randn(3, 3, requires_grad=True)
print(a)
print(b)
y = a @ b
y.backward(torch.ones_like(y))
logger1.info(f'a.grad is : {a.grad}')
logger1.info(f'b.grad is : {b.grad}')def func_a(a):return a @ b
def func_b(b):return a @ b
jacobian_a0 = jacobian(func_a, a[0])
jacobian_a1 = jacobian(func_a, a[1])
logger1.info(f'jacobian_a0 is : {jacobian_a0}')
logger1.info(f'jacobian_a1 is : {jacobian_a1}')
loss_jacobian_a0 = torch.ones_like(func_a(a[0])) @ jacobian_a0
loss_jacobian_a1 = torch.ones_like(func_a(a[1])) @ jacobian_a1
logger1.info(f'loss_jacobian_a0 is : {loss_jacobian_a0}')
logger1.info(f'loss_jacobian_a1 is : {loss_jacobian_a1}')jacobian_b0 = jacobian(func_b, b[:, 0])
jacobian_b1 = jacobian(func_b, b[:, 1])
jacobian_b2 = jacobian(func_b, b[:, 2])
logger1.info(f'jacobian_b0 is : {jacobian_b0}')
logger1.info(f'jacobian_b1 is : {jacobian_b1}')
logger1.info(f'jacobian_b2 is : {jacobian_b2}')
loss_jacobian_b0 = torch.ones_like(func_b(b[:, 0])) @ jacobian_b0
loss_jacobian_b1 = torch.ones_like(func_b(b[:, 1])) @ jacobian_b1
loss_jacobian_b2 = torch.ones_like(func_b(b[:, 2])) @ jacobian_b2
logger1.info(f'loss_jacobian_b0 is : {loss_jacobian_b0}')
logger1.info(f'loss_jacobian_b1 is : {loss_jacobian_b1}')
logger1.info(f'loss_jacobian_b2 is : {loss_jacobian_b2}')

查看全文

http://www.dtcms.com/wzjs/92940.html