在什么网站做贸易好中铁三局招聘官网
1
KMeans聚类
可加群讨论一起学习进步，备注来意
什么是聚类任务
1
无监督机器学习的一种
2
目标将已有数据根据相似度划分到不同的簇
3
簇内样本彼此之间越相似，不同簇的样本之间越不相似，就越好
为什么叫KMeans聚类
1
也可以叫K均值聚类
2
K是最终簇数量，它是超参数，需要预先设定
3
在算法计算中会涉及到求均值
无监督机器学习也是机器学习
是机器学习就涉及到模型求解
KMeans流程举例
随机选择K个簇中心点
1
2
样本被分配到离其最近的中心点
3
4
K个簇中心点根据所在簇样本，以求平均值的方式重新计算重复第2步和第3步直到所有样本的分配不再改变
如何计算样本到中心点的距离
欧氏距离测度 Euclidean Distance Measure
欧氏距离越大，相似度越低
余弦距离测度 Cosine Similarity Measure
夹角越大，余弦值越小，相似度越低
因为是cosine，所以取值范围是-1到1之间，它判断的是向量之间的方向而不是大小；两个向量有同样的方向那么cosine相似度为1，两个向量方向相对成90°那么cosine相似度为0，两个向量正相反那么cosine相似度为-1，和它们的大小无关。
选择Cosine相似度还是欧氏距离
总体来说，欧氏距离体现数值上的绝对差异，而余弦距离体现方向上的相对差异。
例如，统计两部剧的用户观看行为，用户A的观看向量为（0， 1），用户B为（1，0）；此时二者的余弦距离很大，而欧氏距离很小；我们分析两个用户对于不同视频的偏好，更关注相对差异，显
然应当使用余弦距离。
而当我们分析用户活跃度，以登陆次数（单位:次）和平均观看时长
（单位:分钟）作为特征时，余弦距离会认为（1，10）、（10，
100）两个用户距离很近；但显然这两个用户活跃度是有着极大差
异的，此时我们更关注数值绝对差异，应当使用欧氏距离。
cosine相似度更适用于文本
举个例子：
当两篇相似文章长度差距很大、但内容相近时，它们欧氏距离很
大，比如两篇文章相同的词'cricket'一个出现100次，另一个出现10 次；但它们仍然有一个比较小的夹角，所以这时cosine相似度应用会更合适，更小的夹角，更高的相似度。
归一化后选择谁都一样
如果向量的模长是经过归一化的，可以理解为此时向量被投影到了一个长度为1的球面上，这时欧氏距离和余弦距离有着单调的关系，
即
其中 表示欧氏距离，
表示余弦相似度， 表示余弦距离；在向量的模长归一化的场景下，
谁距离最小（相似度最大）就是近邻，那么使用余弦相似度和欧氏
距离的查找近邻结果是相同的。
假设二维空间两个点
将它们归一化为单位向量后
分母是 ，省略
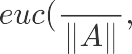
化简后就是
注意，上式中向量归一化前和归一化后不影响
从几何图形上也比较容易看出来，因为余弦看的是方向，与向量大小无关
KMeans算法目标函数
上面的公式既是要去最小化的目标函数，同时也可以作为评价
KMeans聚类效果好坏的评估指标。
KMeans算法不保证找到最好的解
事实上，我们随机初始化选择了不同的初始中心点，我们或许会获得不同的结果，就是所谓的收敛到不同的局部最优；这其实也就从事实上说明了目标函数是非凸函数。
初始中心点，然后从多次运行结果中选择最好的局部最优解。
KMeans算法K的选择
没有所谓最好的选择聚类数的方法，通常是需要根据不同的问题， 人工进行选择的。
肘部法则(Elbow method)
改变聚类数K，然后进行聚类，计算损失函数，拐点处即为推荐的聚类数 (即通过此点后，聚类数的增大也不会对损失函数的下降带来很大的影响，所以会选择拐点)
目标法则
如果聚类本身是为了有监督任务服务的（例如聚类产生features
【譬如KMeans用于某个或某些个数据特征的离散化】然后将KMeans离散化后的特征用于下游任务），则可以直接根据下游任务的metrics进行评估更好；
KMeans空簇的产生原因
1 假设有下面数据
2 迭代过程中
3 进一步更新类中心
实时效果反馈
-
关于KMeans，以下说法不正确的是:
A
需要预先指定K值
B
可以使用肘部法帮助确定K值
C
算法迭代过程中，通过求均值来重新计算K个中心点
D
保证可以求得全局最优解
-
关于距离测度，以下说法不正确的是:
A
欧氏距离测度是常用的距离测度
B
余弦距离测度更适用于文本之间计算相似度
C
样本向量归一化后求欧氏距离数值上等于余弦距离测度
D
样本向量归一化后求欧氏距离最终效果上等价使用余弦距离测
度
答案
1=>D 2=>C
KMeans聚类亦是如此