网站建设十年杜绝模板网络营销企业有哪些公司
介绍
在繁忙的交通中追踪一辆行驶的摩托车并不容易。车辆的移动难以预测,我的眼睛无法捕捉到每一个细微的变化。我必须猜测它要去哪里,然后再次确认,并不断调整我的猜测。这才是真正的挑战:在信息嘈杂且不确定的情况下做出预测。
在实际系统中,情况也是如此。传感器提供的数据并不完美,环境是动态的,物体的运动也并非总是按照预期进行。准确预测并非易事。
这就是我们使用卡尔曼滤波器的原因。
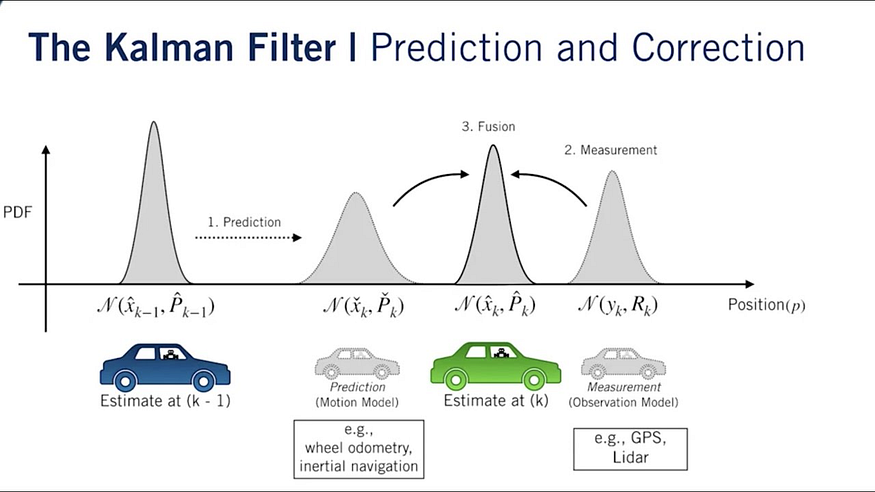
它帮助我预测系统的下一个状态(如位置或速度),测量它,用新数据纠正预测,并重复该过程 - 一步一步变得更加准确。
例如,在多目标追踪中,我首先预测某个目标(例如边界框或骨架)在下一帧中的位置。然后,我会用最新的测量值更新该预测,以确保追踪的可靠性。
在这篇博客中,我将向您展示卡尔曼滤波器解决的问题、它们如何直观地工作以及它们的应用场景——所有这些都不会让您陷入繁重的数学知识中。
核心概念
在深入探讨卡尔曼滤波器本身之前,我们需要了解一些重要的概念。这些概念构成了滤波器实际工作的基础。
卡尔曼滤波器的核心是一个循环:预测 → 测量 → 校正 → 重复。以下是每个部分的分解:
- 状态:这代表您试图估计的内容 - 例如,物体的位置、速度或任何随时间演变的隐藏变量。
- 预测:使用系统通常行为的模型(如恒定速度),您可以估计下一个状态。
- 校正:一旦有新的测量结果,你就需要调整预测以反映新数据。目标是减少预期值与观测值之间的误差。
- 协方差 (可选,但务必牢记):这追踪估计中的不确定性。你可以将其视为衡量滤波器置信度的指标——协方差低表示置信度高,反之亦然。
此外,卡尔曼滤波器依赖于两个关键假设:
- 线性:系统动力学和测量模型被假定为线性的。这意味着我们用涉及加法和乘法的简单方程来描述变化——没有曲线或跳跃之类的非线性行为。
- 高斯(正态)噪声:所有不确定性——无论是来自过程模型还是传感器测量——都被假定遵循正态分布。这一假设允许滤波器仅使用均值和方差来概括不确定性,从而使计算高效且易于处理。
这些假设使得卡尔曼滤波器优雅且计算高效。然而,在打破这些假设的现实世界中,人们会使用扩展卡尔曼滤波器 (EKF) 或无迹卡尔曼滤波器 (UKF) 等扩展算法来代替。
卡尔曼滤波器
该图显示了使卡尔曼滤波器工作的内部循环。
它首先对系统的状态进行一些猜测,并猜测该猜测的不确定性。
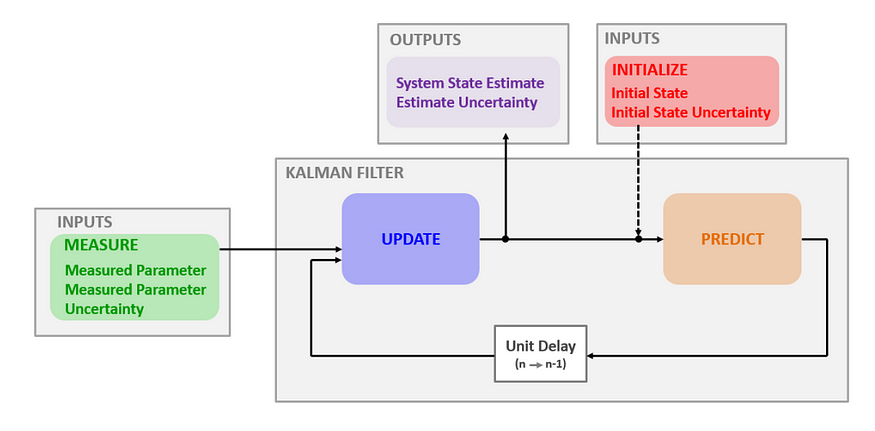
随着新测量值的到来(这些测量值是有噪声的),过滤器会反复执行两个步骤:首先,它根据过去的数据和系统行为预测下一个状态;然后,它使用新的测量值更新该预测。
此修正步骤可改善估计并减少不确定性。
经过改进的估算将成为输出,同时也是下一个循环的输入。结果是一个循环,卡尔曼滤波器不断学习,并实时改进其猜测。
预测步骤
预测步骤就像说:“如果一切按预期进行,我认为我们会处于这个位置。”
在卡尔曼滤波器循环的这一部分,我们采用当前已知的信息(当前状态估计值(以蓝色显示))并使用动态模型来预测系统在下一个时间步骤中可能处于的位置。
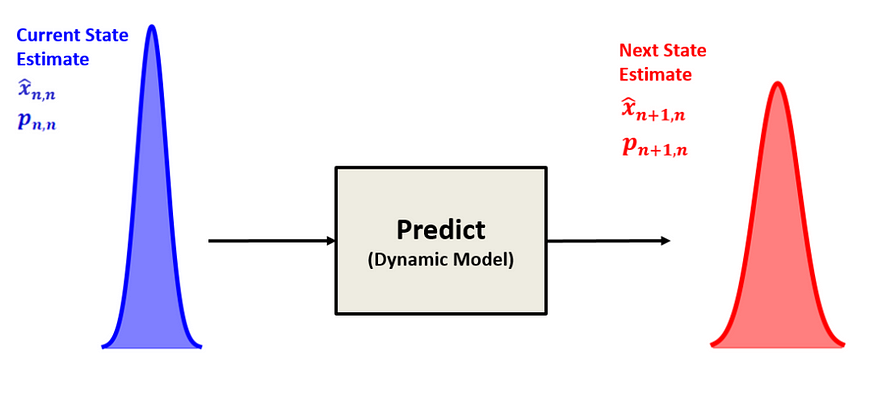
这个当前估计值既包括对系统状态的最佳猜测,也包括我们对该猜测的不确定性程度的衡量。使用该模型(例如,假设物体以恒定速度运动),滤波器会向前投影以获得预测的下一个状态。
但由于现实世界充满不确定性和噪声,我们也会将预测的不确定性带入未来,由于我们在尚未看到任何新事物的情况下进行估计,因此这种不确定性往往会略有增加。
修正步骤
更新步骤是过滤器的说法:“这是我看到实际发生的情况后做出的最佳猜测。”
在预测系统的下一个状态后,卡尔曼滤波器并不会就此止步——它会倾听现实世界的声音。这被称为更新步骤,滤波器会根据最新的测量结果调整其预测。
橙色曲线表示先前的估计值(上一步的预测值)及其估计的不确定性。绿色曲线是来自传感器的新测量值,它也带有自身的测量噪声或不确定性。这是传感器告诉我们的信息——但它并不总是完全可靠的。
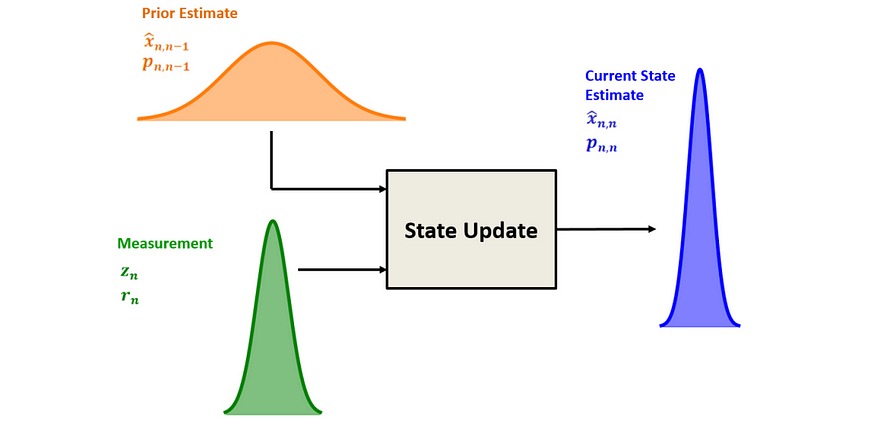
滤波器会比较预测值和测量值,然后根据各自的可信度进行融合。如果传感器数据噪声很大,滤波器会更依赖于自身的预测值。如果预测值较弱但测量值似乎准确,滤波器会赋予新的观测值更大的权重。
结果是对系统当前状态的精确估计(由更清晰的蓝色曲线显示)和更新的置信度衡量标准。
工作流程
卡尔曼滤波器并非一次性的猜测,而是一个动态的估计器。每一步,它都会平衡它所相信的和它所看到的,不断自我修正以保持正轨。
该图将我们所涵盖的所有内容(测量、预测和校正)整合到一个连续的循环中。
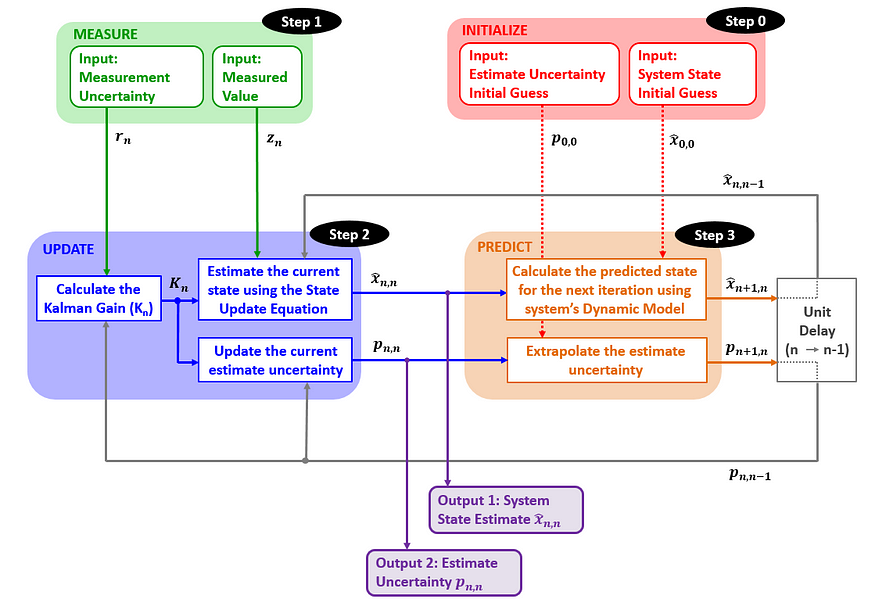
让我们通过 4 个简单的步骤来完成它:
步骤 0:初始化
我们从对系统状态的初步猜测开始,并确定我们对此状态的不确定性。这个猜测不必完美,但它为过滤器的其余操作奠定了基础。
步骤 1:测量
在每个时间步长,系统都会收到一个新的测量值及其不确定性。这可能来自传感器——例如 GPS 读数或摄像头检测——而且通常带有噪声。
第 2 步:更新(更正)
这里是过滤器改进其估计的地方:
- 它计算卡尔曼增益,以决定对测量结果与预测结果的信任程度。
- 然后,使用新的测量值更新当前状态估计。
- 最后,它还更新了不确定性——理想情况下是使其变得更小。
步骤3:预测
使用当前估计值,过滤器使用系统的动态模型(如物理方程)预测下一个状态。
- 它还预测了不确定性,解释了未来增加的不确定性。
然后循环继续进行下一次测量,一遍又一遍地循环预测和更新——使过滤器随着时间的推移变得更智能、更准确。
代码实现
为了更好地理解卡尔曼滤波器的工作原理,让我们用 Python 实现一个基本的一维实现。此版本跟踪具有单一状态的系统——例如估计物体随时间的位置。
我们首先使用几个核心矩阵设置卡尔曼滤波器:
F:转换矩阵,用于模拟状态随时间的变化。例如,在恒速模型中,它可能包含位置和速度。H:观察矩阵,将内部状态映射到我们实际观察到的内容(如传感器读数)。B:控制矩阵,用于模拟任何外部输入(例如加速度)。在许多简单情况下是可选的。Q:过程噪声协方差,它解释了模型本身的不确定性——例如物体意外改变速度的情况。R:测量噪声协方差,用于捕捉传感器的噪声程度。P:估计误差协方差,表示我们对当前状态估计的信心程度。x:状态向量,也就是我们试图估计的(例如,物体的当前位置)。
预测步骤
<span style="color:rgba(0, 0, 0, 0.8)"><span style="background-color:#ffffff"><span style="background-color:#f9f9f9"><span style="color:#242424">自我.x = 自我.F @ 自我.x + 自我.B @ u
自我.P = 自我.F @ 自我.P @ 自我.FT + 自我.Q</span></span></span></span>这是它的作用:
- 第一行通过应用运动模型()和可选的控制输入( )来更新状态估计。它的基本意思是:“根据物体现在的位置,我认为它接下来会在这里。”
FB @ u - 第二行更新不确定性(
P)。它会向前传播,并且我们会添加Q不确定性以解释转换过程中任何增加的过程噪声。
在此阶段,过滤器已做出最佳猜测,但尚未看到任何新数据。
更新步骤
<span style="color:rgba(0, 0, 0, 0.8)"><span style="background-color:#ffffff"><span style="background-color:#f9f9f9"><span style="color:#242424">y = z - self.H @ self.x
S = self.R + self.H @ self.P @ self.HT
K = self.P @ self.HT @ np.linalg.inv(S)
self.x = self.x + K @ y
I = np.eye(self.state_dim)
self.P = (I - K @ self.H) @ self.P @ (I - K @ self.H).T + K @ self.R @ KT</span></span></span></span>让我们来分析一下:
y是测量残差——我们观察到的结果与预期结果之间的差异。这告诉我们预测结果的偏差有多大。S是残差协方差,表示预测和测量中的不确定性。K是卡尔曼增益,它决定了我们应该在多大程度上相信测量值与预测值。
然后我们应用修正:
x使用卡尔曼增益和残差来更新状态——使估计值更接近测量值。- 协方差
P也进行了更新,以反映纳入新观察后信心的提高。
这是整个实现
<span style="color:rgba(0, 0, 0, 0.8)"><span style="background-color:#ffffff"><span style="background-color:#f9f9f9"><span style="color:#242424"><span style="color:#aa0d91">class </span> KalmanFilter : <span style="color:#aa0d91">def </span> __init__ (
<span style="color:#5c2699"> self, transition_matrix: NDArray[np.float64], observation_matrix: NDArray[np.float64], control_matrix: NDArray[np.float64] | <span style="color:#aa0d91">None</span> = <span style="color:#aa0d91">None</span> , process_noise_cov: NDArray[np.float64] | <span style="color:#aa0d91">None</span> = <span style="color:#aa0d91">None</span> , measurements_noise_cov: NDArray[np.float64] | <span style="color:#aa0d91">None</span> = <span style="color:#aa0d91">None</span> , assess_cov: NDArray[np.float64] | <span style="color:#aa0d91">None</span> = <span style="color:#aa0d91">None</span> , initial_state: NDArray[np.float64] | <span style="color:#aa0d91">None</span> = <span style="color:#aa0d91">None</span> ,</span> ): <span style="color:#c41a16">"""初始化卡尔曼滤波器。""" </span><span style="color:#aa0d91">if</span> transition_matrix <span style="color:#aa0d91">is </span> <span style="color:#aa0d91">None </span> <span style="color:#aa0d91">or</span> observation_matrix <span style="color:#aa0d91">is </span> <span style="color:#aa0d91">None</span> : <span style="color:#aa0d91">raise</span> ValueError( <span style="color:#c41a16">"系统动力学必须用转换和观察矩阵来定义。"</span> ) self.state_dim = transition_matrix.shape[ <span style="color:#1c00cf">1</span> ] self.measure_dim = observation_matrix.shape[ <span style="color:#1c00cf">0</span> ] self.F = transition_matrix self.H = observation_matrix self.B = np.zeros((self.state_dim, <span style="color:#1c00cf">1</span> ))<span style="color:#aa0d91">如果</span>control_matrix<span style="color:#aa0d91">为</span> <span style="color:#aa0d91">None </span> <span style="color:#aa0d91">else</span> control_matrix self.Q = np.eye(self.state_dim)<span style="color:#aa0d91">如果</span>process_noise_cov<span style="color:#aa0d91">为</span> <span style="color:#aa0d91">None </span> <span style="color:#aa0d91">else</span> process_noise_cov self.R = np.eye(self.measure_dim)<span style="color:#aa0d91">如果</span>measurements_noise_cov<span style="color:#aa0d91">为</span> <span style="color:#aa0d91">None </span> <span style="color:#aa0d91">else</span> measurements_noise_cov self.P = np.eye(self.state_dim)<span style="color:#aa0d91">如果</span>assesse_cov<span style="color:#aa0d91">为</span> <span style="color:#aa0d91">None </span> <span style="color:#aa0d91">else</span> assesse_cov self.x = np.zeros((self.state_dim, <span style="color:#1c00cf">1</span> ))<span style="color:#aa0d91">如果</span>initial_state<span style="color:#aa0d91">为</span> <span style="color:#aa0d91">None </span> <span style="color:#aa0d91">else</span> initial_state <span style="color:#aa0d91">def </span> predict ( <span style="color:#5c2699">self, control_input: NDArray[np.float64] | <span style="color:#5c2699">float</span> = <span style="color:#1c00cf">0</span></span> ) -> NDArray[np.float64]: <span style="color:#c41a16">"""预测下一个状态并更新估计协方差。"""</span>u = np.array([[control_input]]) <span style="color:#aa0d91">if</span> np.isscalar(control_input) <span style="color:#aa0d91">else</span> control_inputself.x = self.F @ self.x + self.B @ u self.P = self.F @ self.P @ self.FT + self.Q <span style="color:#aa0d91">return</span> self.x <span style="color:#aa0d91">def </span> update ( <span style="color:#5c2699">self, measurements: <span style="color:#5c2699">float</span> | NDArray[np.float64]</span> ) -> <span style="color:#aa0d91">None</span> : <span style="color:#c41a16">"""根据新的测量结果更新卡尔曼滤波器。"""</span>z = np.array([[measurement]]) <span style="color:#aa0d91">if</span> np.isscalar(measurement) <span style="color:#aa0d91">else</span> measurements.reshape(- <span style="color:#1c00cf">1</span> , <span style="color:#1c00cf">1</span> ) y = z - self.H @ self.x <span style="color:#007400"># 测量残差</span>S = self.R + self.H @ self.P @ self.HT <span style="color:#007400"># 残差协方差</span>K = self.P @ self.HT @ np.linalg.inv(S) <span style="color:#007400"># 卡尔曼增益</span>self.x = self.x + K @ y I = np.eye(self.state_dim) self.P = (I - K @ self.H) @ self.P @ (I - K @self.H).T + K@self.R@KT</span></span></span></span>演示
这是我用于演示的代码:
<span style="color:rgba(0, 0, 0, 0.8)"><span style="background-color:#ffffff"><span style="background-color:#f9f9f9"><span style="color:#242424">dt = <span style="color:#1c00cf">1.0</span> / <span style="color:#1c00cf">60</span>F = np.array([[ <span style="color:#1c00cf">1</span> , dt, <span style="color:#1c00cf">0</span> ], [ <span style="color:#1c00cf">0</span> , <span style="color:#1c00cf">1</span> , dt], [ <span style="color:#1c00cf">0</span> , <span style="color:#1c00cf">0</span> , <span style="color:#1c00cf">1</span> ]])
H = np.array([[ <span style="color:#1c00cf">1</span> , <span style="color:#1c00cf">0</span> , <span style="color:#1c00cf">0</span> ]])
Q = np.array([[ <span style="color:#1c00cf">0.05</span> , <span style="color:#1c00cf">0.05</span> , <span style="color:#1c00cf">0.0</span> ], [ <span style="color:#1c00cf">0.05</span> , <span style="color:#1c00cf">0.05</span> , <span style="color:#1c00cf">0.0</span> ], [ <span style="color:#1c00cf">0.0</span> , <span style="color:#1c00cf">0.0</span> , <span style="color:#1c00cf">0.0</span> ]])
R = np.array([[ <span style="color:#1c00cf">0.5</span> ]]) x_vals = np.linspace(- <span style="color:#1c00cf">10</span> , <span style="color:#1c00cf">10</span> , <span style="color:#1c00cf">100</span> )
true_values = -(x_vals** <span style="color:#1c00cf">2</span> + <span style="color:#1c00cf">2</span> * x_vals - <span style="color:#1c00cf">2</span> )
noisy_measurements = true_values + np.random.normal( <span style="color:#1c00cf">0</span> , <span style="color:#1c00cf">2</span> , <span style="color:#1c00cf">100</span> ) kf = KalmanFilter(transition_matrix=F, observation_matrix=H, process_noise_cov=Q, measurements_noise_cov=R)
predictions = [] <span style="color:#aa0d91">for</span> z <span style="color:#aa0d91">in</span> noisy_measurements:预测 = H @ kf.predict(control_input= <span style="color:#1c00cf">5</span> )预测.append(prediction.item()) kf.update(z) plt.plot(true_values, label= <span style="color:#c41a16">'真值'</span> )
plt.plot(noisy_measurements, label= <span style="color:#c41a16">'测量值'</span> )
plt.plot(predictions, label= <span style="color:#c41a16">'卡尔曼滤波器预测'</span> )
plt.legend()
plt.title( <span style="color:#c41a16">"卡尔曼滤波器演示"</span> )
plt.show() </span></span></span></span>结果:
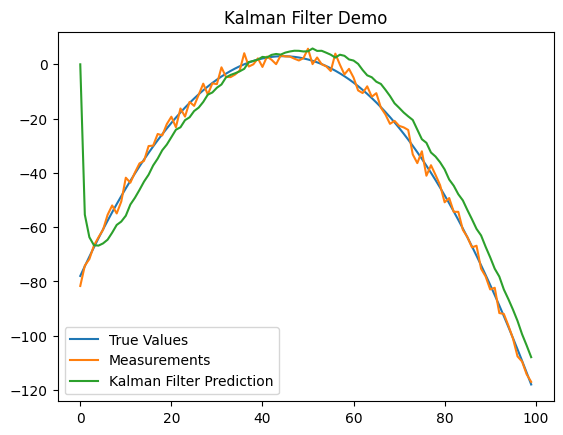
概括
在本篇博文中,我们探讨了卡尔曼滤波器背后的原理——这是一种强大的算法,能够帮助我们在不确定的环境中做出更准确的预测。我们以一个追踪摩托车的真实案例为例,分解了该滤波器的两个核心步骤:预测和校正。
您了解了卡尔曼滤波器的工作原理:
- 使用模型预测接下来会发生什么,
- 根据新的、嘈杂的测量结果进行预测的更新,
- 并不断完善其估计,随着时间的推移变得更加准确。
我们用清晰的图表将每个步骤可视化——从初始状态,到测量更新,再到整个周期——使数学变得易于理解,而无需深入研究方程式。
无论您是构建跟踪系统、融合传感器数据,还是只是好奇机器如何智能地“猜测”事物,卡尔曼滤波器都是需要理解的基础工具。

