当前位置：首页 > wzjs >正文

广州品牌设计网站建设宣传推广图片

wzjs 2025/8/16 6:13:34

广州品牌设计网站建设,宣传推广图片,网站使用微软雅黑,struts动态网站开发综合实训总结一、二叉树的遍历“遍历”就是按某种规则依次访问树中的每个节点，确保每个节点都被访问一次且只访问一次遍历：前序中序后序（深度优先），层序（广度优先）类型遍历方法特点深度优先遍历前序、中…

一、二叉树的遍历

“遍历”就是按某种规则 依次访问树中的每个节点，确保 每个节点都被访问一次且只访问一次

遍历：前序中序后序（深度优先），层序（广度优先）

类型	遍历方法	特点
深度优先遍历	前序、中序、后序	类似“先走到尽头，再回头”
广度优先遍历	层序遍历（Level-order）	按层访问，从上到下

二、深度优先遍历

任何一个二叉数、都要看做3个部分：

1、根节点；2、左子树；3、右子树。

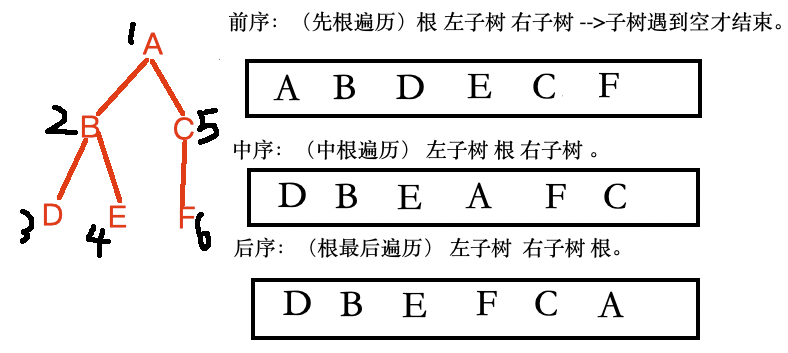
前序：（先根遍历）根左子树右子树 -->子树遇到空才结束，用途：复制树、表达式树转前缀表达式等

中序：（中根遍历）左子树根右子树，用途：如果是二叉搜索树（BST），中序遍历输出的是升序序列

后序：（中根遍历）左子树右子树根，用途：删除树（先删子树再删根）、表达式树转后缀表达式等

示意图：

遍历方式	访问顺序
前序	A B D E C F
中序	D B E A C F
后序	D E B F C A

二叉树的前序遍历实现（利用递归的思想）：

代码实现：

1、二叉树的初始化

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include <string.h>#define Init_Capcity 5
typedef char BTDataType;
typedef struct BNTreeNode
{BTDataType _data;struct BNTreeNode* left_child;struct BNTreeNode* right_child;
}BNTreeNode;BNTreeNode* BNTreeNode_Init(){BNTreeNode* pt = (BNTreeNode*)malloc(sizeof(BNTreeNode));pt ->left_child =NULL;pt->right_child = NULL;return pt;
}

2、新增子节点

//新增子节点
BNTreeNode* BuyTreeNode(BTDataType val){BNTreeNode* NewNode = (BNTreeNode*)malloc(sizeof(BNTreeNode));NewNode->_data = val;NewNode->left_child = NULL;NewNode->right_child = NULL;return NewNode;
}

3、二叉树的前序遍历以及主函数的实现

void BNTraverse(BNTreeNode* root){if(root == NULL){return;}printf("%c  ",root->_data);BNTraverse(root->left_child);BNTraverse(root->right_child);
}int main(){BNTreeNode* Root = BNTreeNode_Init();Root->_data = 'A';Root->left_child = BuyTreeNode('B');Root->right_child = BuyTreeNode('C');(Root->left_child)->left_child = BuyTreeNode('D');(Root->left_child)->right_child = BuyTreeNode('E');(Root->right_child)->left_child = BuyTreeNode('F');BNTraverse(Root);
}

4、二叉树的中序，后序遍历

void InOrder(BNTreeNode* root){if(root == NULL){return;}InOrder(root->left_child);printf("%c  ",root->_data);InOrder(root->right_child);
}
void PostOrder(BNTreeNode* root){if(root == NULL){return;}PostOrder(root->left_child);PostOrder(root->right_child);printf("%c  ",root->_data);
}

输出结果：

A B D NULL NULL E NULL NULL C F NULL NULL NULL
NULL D NULL B NULL E NULL A NULL F NULL C NULL
NULL NULL D NULL NULL E B NULL NULL F NULL C A

利用类似的递归思路求解，二叉树的元素个数，叶节点个数，深度等

1、二叉树元素的个数 -->遇到空节点停止

//两种方法
void TreeSize(BNTreeNode* root,int* psize){if(root == NULL){return;}//static int size = 0; //静态变量只有当前文件能使用(*psize)++;TreeSize(root->left_child,psize);TreeSize(root->right_child,psize);
}
//不需要额外参数
int TreeSize(BNTreeNode* root){if(root == NULL){return 0;}else{return 1+TreeSize(root->left_child)+TreeSize(root->right_child);}
}

2、叶节点个数-->遍历到无子节点（叶节点）

//统计叶节点个数
int TreeLeafSize(BNTreeNode* root){if(root == NULL){return 0;}if(root->left_child == NULL && root->right_child == NULL){return 1;}return TreeLeafSize(root->left_child)+TreeLeafSize(root->right_child);
}

3、需要比较左右子树的深度 -->遇到空节点停止

int TreeDepth(BNTreeNode* root) {if (root == NULL) {return 0;}int left_depth = TreeDepth(root->left_child);int right_depth = TreeDepth(root->right_child);return 1 + (left_depth > right_depth ? left_depth : right_depth);
}