网站建设著作权网络营销成功的案例

1 归并排序

时间复杂度：O(N*logN)
空间复杂度：O(N)
稳定性：稳定

归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中外排序问题。

1.1归并排序思想

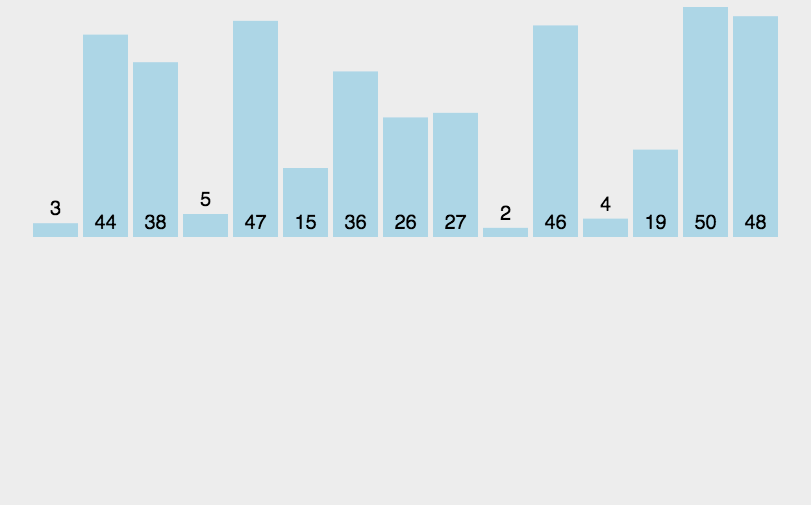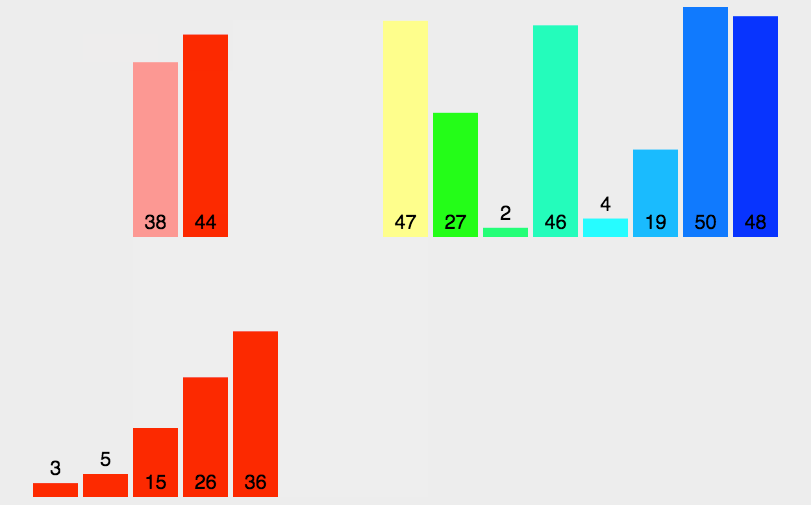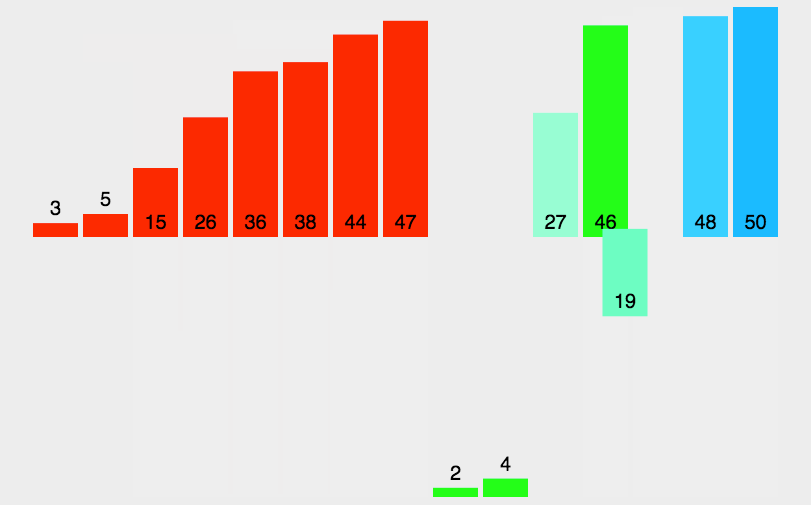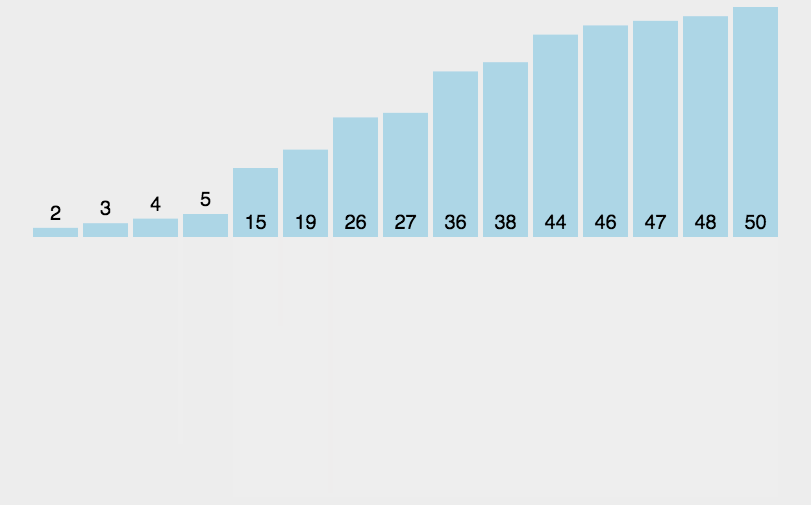
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide andConquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

子序列问题就是合并两个有序数组：
设有a、b数组加临时数组temp，指针n1、n2，n1一开始指向a[0],n2一开始指向b[0],逐个比较，小的放入temp数组中，然后小的指针++，然后再继续比较

1.2归并排序代码实现

void _MergeSort(int* a, int begin, int end, int* temp)
{if (begin >= end)return;int mid = (begin + end) / 2;_MergeSort(a, begin, mid, temp);	//取出第一个数组区间_MergeSort(a, mid + 1, end, temp);	//取出第二个数组区间//下面为单趟归并排序，也是子问题（合并两个有序数组）int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){temp[i] = a[begin1];i++;begin1++;}else{temp[i] = a[begin2];i++;begin2++;}}while (begin1 <= end1)//这两个while有且仅有一个成立，即为把剩下的数插入到temp末尾{temp[i] = a[begin1];i++;begin1++;}while (begin2 <= end2){temp[i] = a[begin2];i++;begin2++;}// 拷贝回原数组 -- 归并哪部分就拷贝哪部分回去memcpy(a + begin, temp + begin, (end - begin + 1) * sizeof(int));
}void MergeSort(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");return;}_MergeSort(a, 0, n - 1, temp);free(temp);temp = NULL;
}

2非递归归并排序

2.1非递归归并排序代码实现

void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){// gap个数据  gap个数据归并for (int j = 0; j < n; j += 2 * gap){// 归并 取小的尾插int begin1 = j, end1 = j + gap - 1;int begin2 = j + gap, end2 = j + 2 * gap - 1;// 第一组越界if (end1 >= n){printf("[%d,%d]", begin1, n - 1);break;}// 第二组全部越界if (begin2 >= n){printf("[%d,%d]", begin1, end1);break;}// 第二组部分越界if (end2 >= n){// 修正一下end2，继续归并end2 = n - 1;}printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);int i = j;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}// 拷贝回原数组 -- 归并哪部分就拷贝哪部分回去memcpy(a + j, tmp + j, (end2 - j + 1) * sizeof(int));}gap *= 2;printf("\n");}free(tmp);tmp = NULL;
}