营销型网站建设中坚站百度的营销策略

力扣链接

力扣

题目描述：

我们正在玩一个猜数游戏，游戏规则如下：

1. 我从 1 到 n 之间选择一个数字。
2. 你来猜我选了哪个数字。
3. 如果你猜到正确的数字，就会 赢得游戏 。
4. 如果你猜错了，那么我会告诉你，我选的数字比你的 更大或者更小 ，并且你需要继续猜数。
5. 每当你猜了数字 x 并且猜错了的时候，你需要支付金额为 x 的现金。如果你花光了钱，就会 输掉游戏 。

给你一个特定的数字 n ，返回能够 确保你获胜 的最小现金数，不管我选择那个数字 。

 

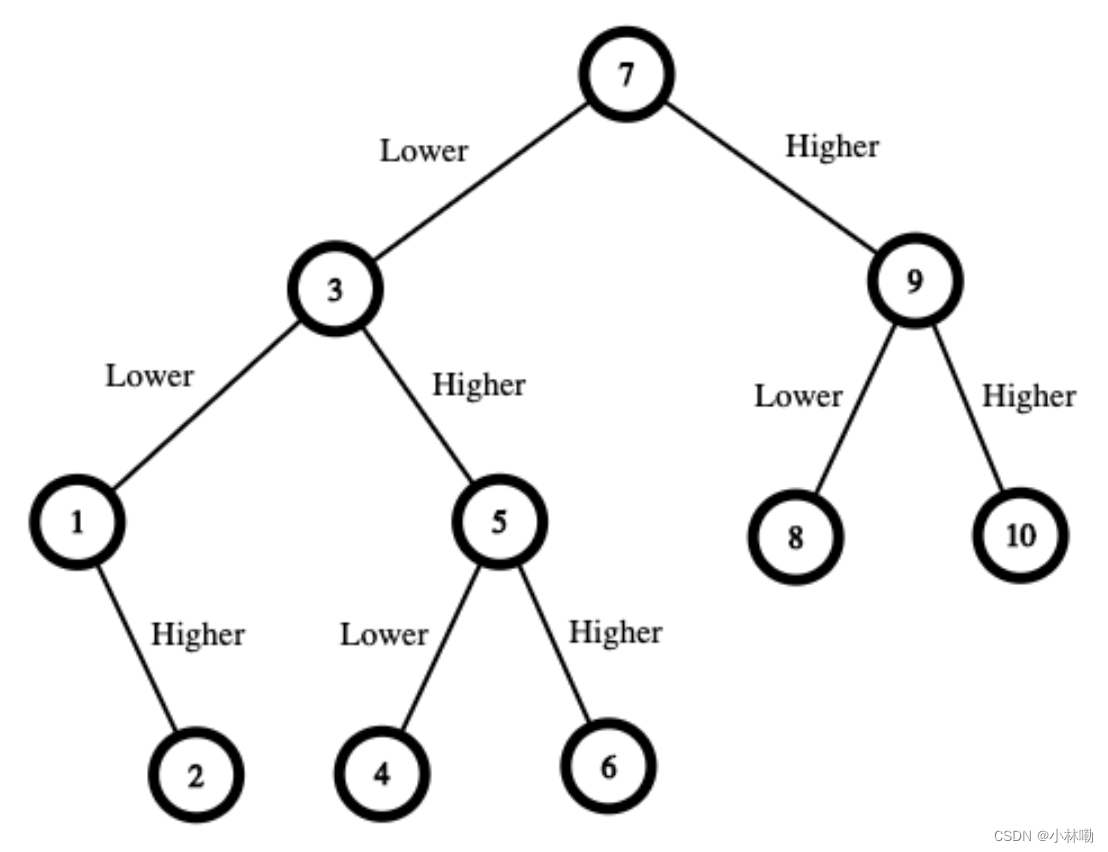
输入：n = 10
输出：16
解释：制胜策略如下：
- 数字范围是 [1,10] 。你先猜测数字为 7 。- 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $7 。- 如果我的数字更大，则下一步需要猜测的数字范围是 [8,10] 。你可以猜测数字为 9 。- 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $9 。- 如果我的数字更大，那么这个数字一定是 10 。你猜测数字为 10 并赢得游戏，总费用为 $7 + $9 = $16 。- 如果我的数字更小，那么这个数字一定是 8 。你猜测数字为 8 并赢得游戏，总费用为 $7 + $9 = $16 。- 如果我的数字更小，则下一步需要猜测的数字范围是 [1,6] 。你可以猜测数字为 3 。- 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $3 。- 如果我的数字更大，则下一步需要猜测的数字范围是 [4,6] 。你可以猜测数字为 5 。- 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $5 。- 如果我的数字更大，那么这个数字一定是 6 。你猜测数字为 6 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。- 如果我的数字更小，那么这个数字一定是 4 。你猜测数字为 4 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。- 如果我的数字更小，则下一步需要猜测的数字范围是 [1,2] 。你可以猜测数字为 1 。- 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $1 。- 如果我的数字更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $7 + $3 + $1 = $11 。
在最糟糕的情况下，你需要支付 $16 。因此，你只需要 $16 就可以确保自己赢得游戏。

解法：

1.记忆化递归：

简单地思路梳理：

我们可以枚举1到n中的每一个数字，记为x，那么分为两种情况，猜中了和没猜中       

• 假如 x 正好是选中的数，那么，付出的代价为 0；
• 假如 x 不是选中的数，那么，付出的代价为 x，然后，我们会得到提示，选中的数比 x 大还是比 x 小：
  • 假如比 x 小，我们只要求得 1 到 x-1 的最小代价，再加上 x 就能得到猜 x 时的最小代价；
  •  假如比 x 大，我们只要求得 x+1 到 n 的最小代价，再加上 x 就能得到猜 x 时的最小代价；
  • 而选中的数有可能在 x 的左边，也可能在 x 的右边，为了保证我们能够赢得游戏，我们需要备用的现金应该是左右两边的最小代价的最大值再加上 x 本身。

当我们枚举完这些 x 后，取其中的最小值就是我们需要备用的现金。

所以，我们可以得到递推公式：

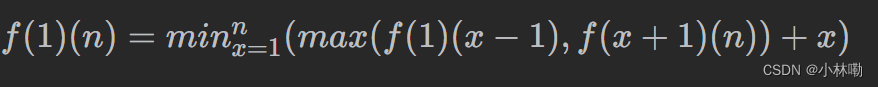 你会发现存在很多重复的计算，比如，计算 f(1)(4) 的时候会计算 f(1)(2) 和 f(1)(3)，而计算 f(1)(3) 的时候也会计算 f(1)(2)，所以，我们可以加上缓存记录已经计算过的数值，这就是记忆化搜索

class Solution {public int getMoneyAmount(int n) {int[][] memo = new int[n + 2][n + 2];return dfs(1, n, memo);}private int dfs(int start, int end, int[][] memo) {if (start >= end) {return 0;}if (memo[start][end] != 0) {return memo[start][end];}int ans = Integer.MAX_VALUE;for (int k = start; k <= end; k++) {ans = Math.min(ans, Math.max(dfs(start, k - 1, memo), dfs(k + 1, end, memo)) + k);}return memo[start][end] = ans;}
}

2.动规（区间DP）：

再上一步的记忆化递归中，我们发现，每次计算区间[x,y]都依赖与更小的区间，那么调整区间的计算顺序，我们不妨先计算小的区间，这样在计算大的区间的时候就不必重新计算小的区间了。

• 状态定义：dp[i][j]表示选中的数在 [i,j] 之间时能够确保获胜需要备用的现金数；
• 状态转移：dp[i][j]=min{k=i->j}(max(dp[i][k-1], dp[i][k+1]) + k);
• 初始值：对于只有一个数时，选中的数肯定就是这个数，代价为0，所以，初始值为 dp[i][i] = 0，Java中不需要特殊处理；
• 返回值：dp[1][n]；

典型的区间dp的写法：

枚举长度从小到大：

class Solution {public int getMoneyAmount(int n) {// dp[i][j]表示选择的数在[i,j]之间时能够确保获胜的最小钱数// dp[i][j]=min{k=i->j}(max(dp[i][k-1], dp[i][k+1]) + k)int[][] dp = new int[n + 2][n + 2];for (int len = 2; len <= n; len++) {//长度从小到大枚举for (int i = 1; i <= n - len + 1; i++) {//从小到大，也就是举例 [1,1+len]  [2,2+len]这样int j = i + len - 1;int min = Integer.MAX_VALUE;for (int k = i; k <= j; k++) {//注意k在后面的整体之中，为什么加k，因为是没选中k，所以要付出代价为k//然后比较原来的数据和当前没选中需要花费的最大的代价，取最大代价中最小的min = Math.min(min, Math.max(dp[i][k - 1], dp[k + 1][j]) + k);}dp[i][j] = min;}}return dp[1][n];}
}

代码说明：

        注意，for循环中的len是我们枚举的长度，不是整个数字n的长度。