工信局网站备案查询北京推广

1.二叉搜索树转双向链表

题目链接：BSTreeTransformList


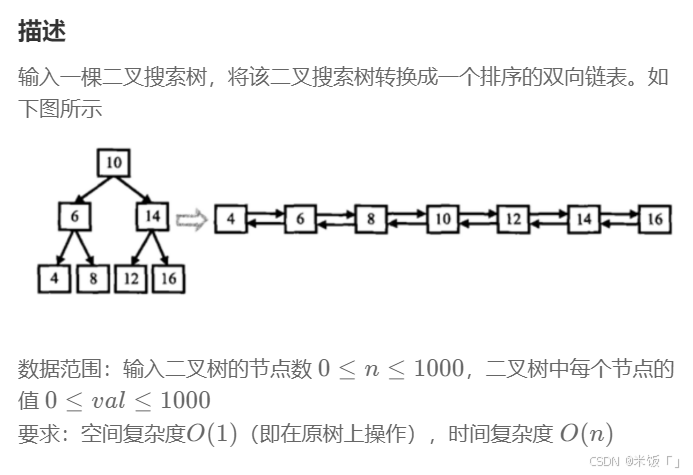
题目要求的是将一个二叉搜索树转换成一个如上图的排序双向链表。并且不能创建新节点，只能在原链表上进行操作。注意：这个链表不是循环链表。

🍋🍋做这道题的思路：
由于转换后的双向链表是有序的，所以这道题需要用中序遍历来实现。需要用到一个cur节点指针和prev节点指针；cur指针用来指向当前遍历到的节点，当cur要往下一个节点移动时先将值给给prev，然后cur再中序遍历下一个节点。

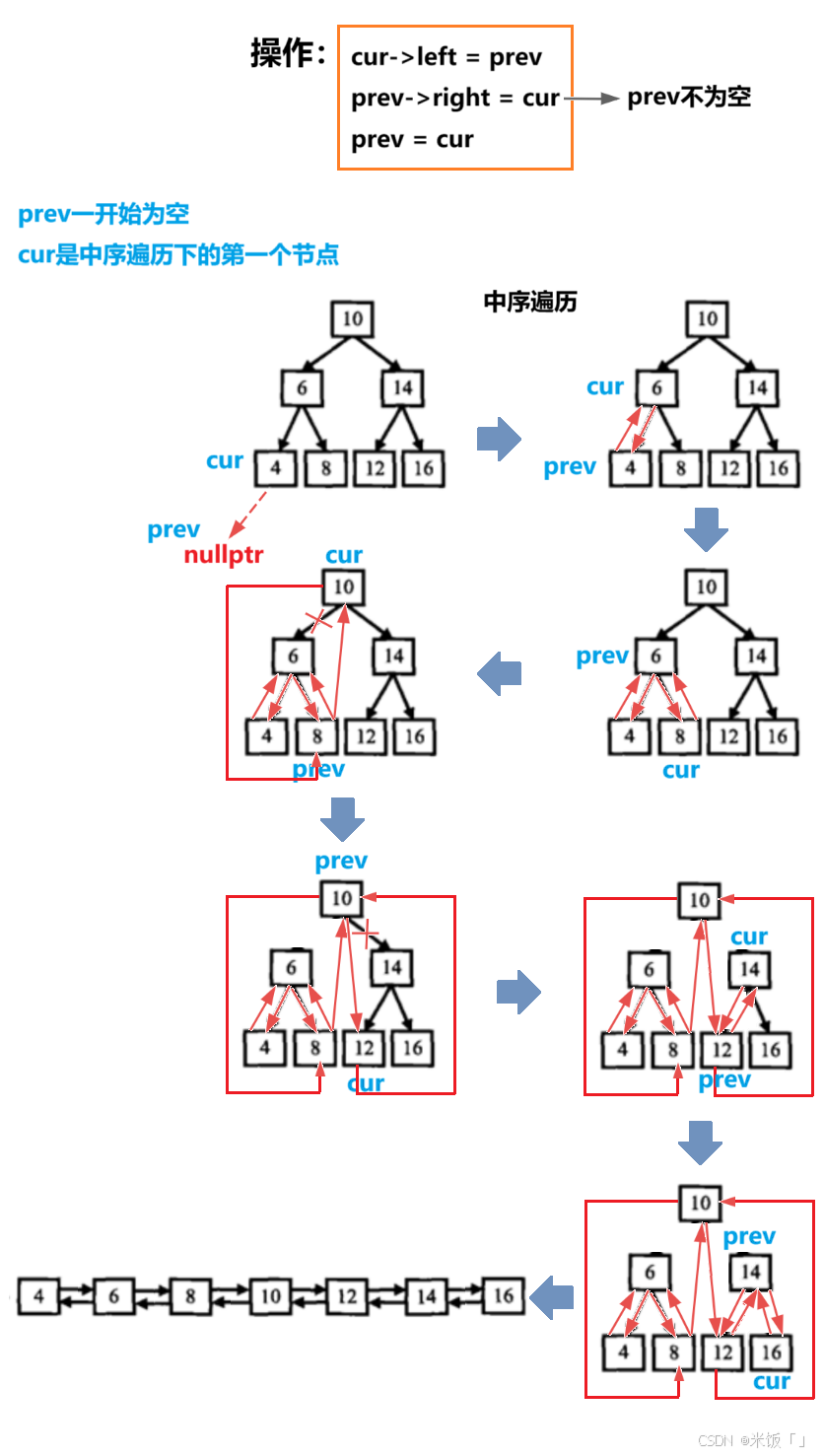
假设已经提前定义好了节点的结构，则代码实现如下：

class Solution 
{
private:void InOrderCovert(TreeNode* cur,TreeNode*& prev){if(cur == nullptr)return;InOrderCovert(cur->left,prev);cur->left = prev;if(prev != nullptr)prev->right = cur;prev = cur;InOrderCovert(cur->right,prev);}
public:TreeNode* Convert(TreeNode* pRootOfTree) {TreeNode* cur = pRootOfTree;TreeNode* prev = nullptr;InOrderCovert(cur,prev);TreeNode* head = pRootOfTree;while(head && head->left){head = head->left;}return head;}
};

注意：代码中最重要的一点就是InOrderCovert函数的prev参数要给引用，这样才能让prev记录下cur中序遍历下的前一节点指针。若不明白可以画递归展开图理解。

2.根据一棵树的前序与中序遍历构造二叉树

题目链接：PreAndInConstructBinaryTree

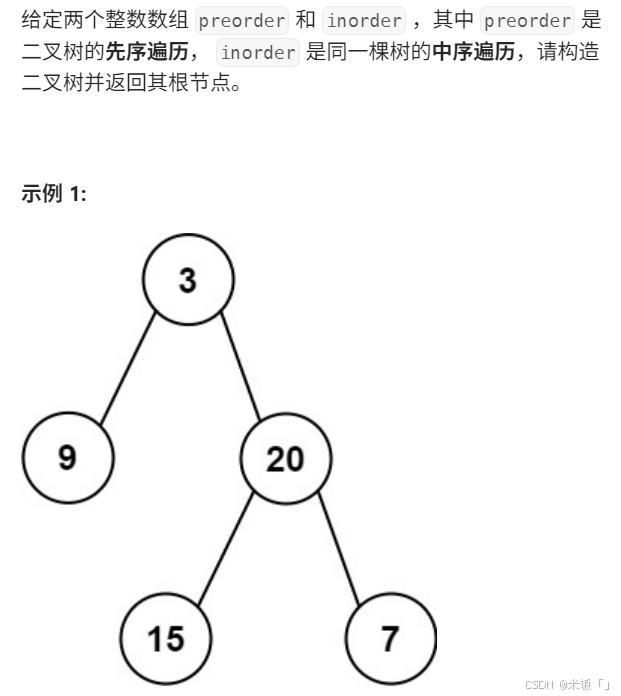
🍊🍊做这题的重要思路：
★前序确定根节点，中序分隔确定左右子树。
●递归的子问题：就是通过前序确定根后，在中序里分隔出左右子树，则中序分割出的左子树又可以通过前序的下一个值来确定子树的根，紧接着就又是分割左右子树，这就是递归的子问题；当左子树递归完毕后，就是右子树的递归；如此，就可以将这棵二叉树给构造出来啦。
●递归的结束条件：通过前序确定根以后可以在中序中分割出左右子树的区间，则当递归到区间不存在时，说明左右子树已经为空，这时就递归结束。

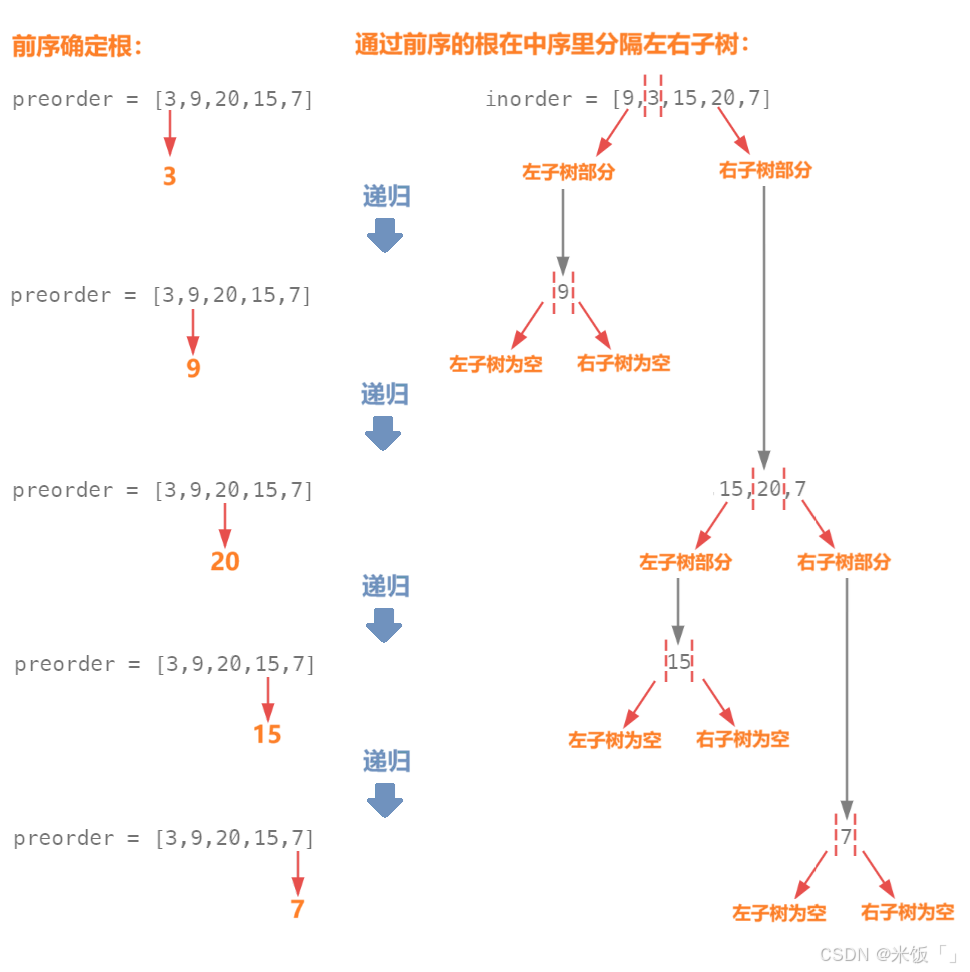
假设已经提前定义好了节点的结构，则代码实现如下：(注意题目中所给的提示)

class Solution 
{
private:TreeNode* _build(vector<int>& preorder, vector<int>& inorder, int& prei, int inbegin, int inend){//递归的结束条件是分割的区间不存在if(inbegin > inend)return nullptr;int rooti = inbegin;//通过前序根节点的值，在中序中找到该值的位置while(rooti <= inend){if(preorder[prei] == inorder[rooti]){break;}rooti++;}//前序确定根TreeNode* root = new TreeNode(preorder[prei++]);//中序序列划分为: [inbegin,rooti-1] rooti [rooti+1,inend]//先递归左子树，回来再递归右子树，并连接为root的左右子树root->left = _build(preorder, inorder, prei, inbegin, rooti-1);root->right = _build(preorder, inorder, prei, rooti+1, inend);return root;}
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int i = 0;//注意:[inbegin,inend]是左闭右闭区间TreeNode* root = _build(preorder,inorder,i,0,inorder.size()-1);return root;}
};

上面的代码中需要注意子函数_build中的参数prei要用引用的形式，因为在整个递归过程中，前序数组序列都是同一个数组的下标在变化。同理：前序和中序两个序列能将二叉树构造出来；则中序和后序也能将二叉树给构造出来。只是后序要倒着从后往前访问：后序倒着访问到根以后，紧接着就是右子树的根节点，然后才是左子树的根节点。

3.二叉树的前序遍历(非递归迭代)

题目链接：PreOrderByIteration

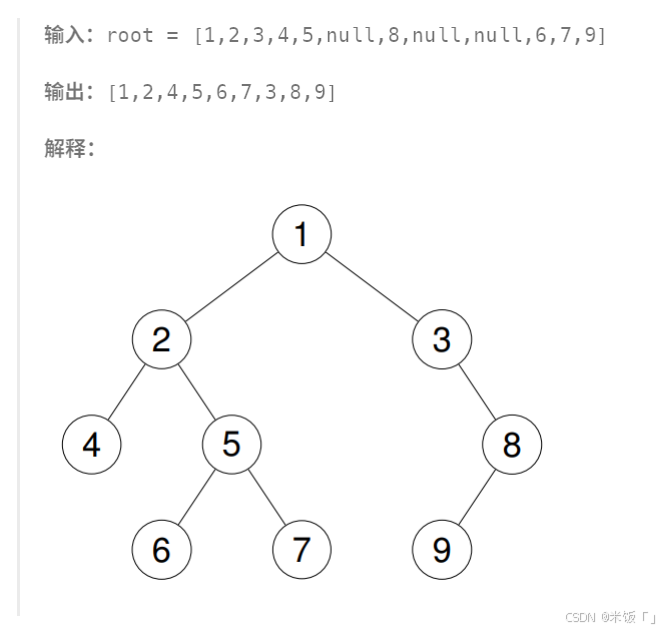
🍐🍐通过非递归迭代来实现二叉树的前序遍历思路如下：

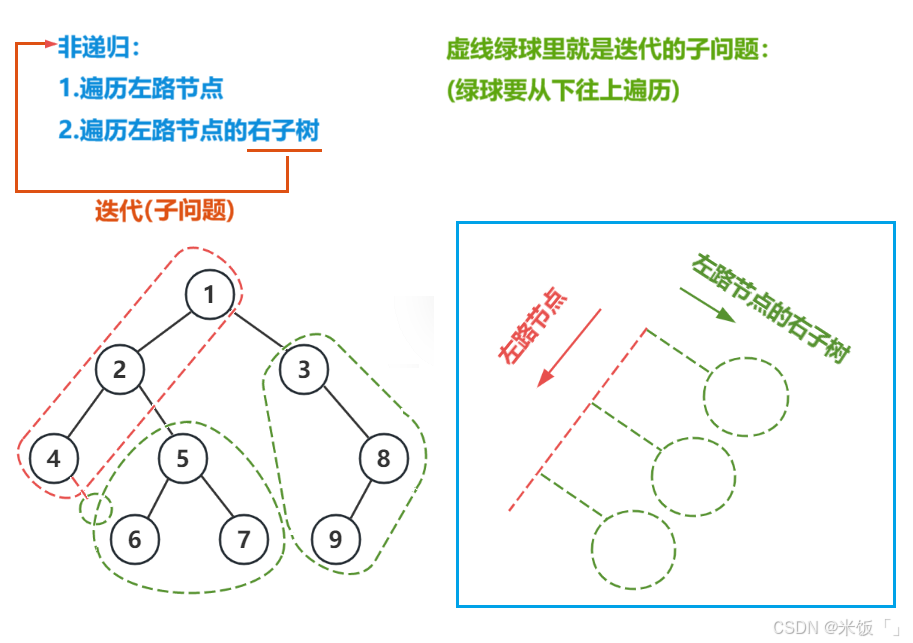
先遍历左路节点，然后要从下往上遍历左路节点的右子树；进入到右子树后，就是迭代的子问题：即在右子树中也是先遍历左路节点，然后遍历左路节点的右子树。代码实现如下：

class Solution 
{
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> s;vector<int> v;TreeNode* cur = root;while(cur != nullptr || !s.empty()){//遍历左路节点while(cur != nullptr){v.push_back(cur->val);s.push(cur);cur = cur->left;}TreeNode* top = s.top();s.pop();//迭代遍历左路节点的右子树cur = top->right;}return v;}
};

这道题利用了栈的性质来实现从下往上遍历左路节点的右子树。而右子树里就是迭代的子问题。同理：对于非递归的中序遍历只不过是根左右子树的访问时机不同而已，大家可以自己下去尝试。

4.二叉树的后序遍历(非递归迭代)

题目链接：PostOrderByIteration



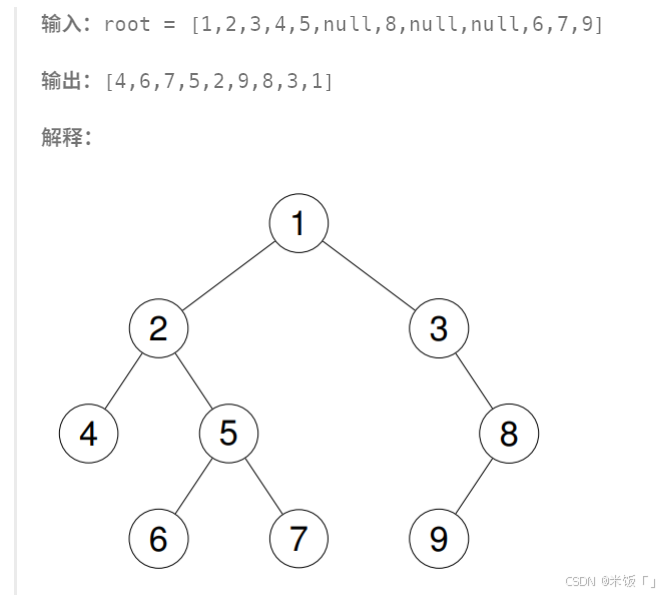
二叉树的后序遍历通过非递归迭代实现相较于前序和中序就比较麻烦，因为后序是左子树右子树根的顺序访问二叉树。

🍑🍑做这题的一个比较简单的思路是：
★用一个prev指针记录上一个访问的节点。
首先要把左路节点依次入栈，当左路节点都入栈以后，才开始根据左右根的次序访问节点；但每当访问栈里面的节点时，都要先判断这个节点的右子树部分是否存在 或者 是否已经访问过？如果右子树为空 或者 右子树部分已经访问过，才能访问栈顶的节点(就相当于访问当前子树的根节点)。所以这里要用prev指针记录上一个访问的节点：

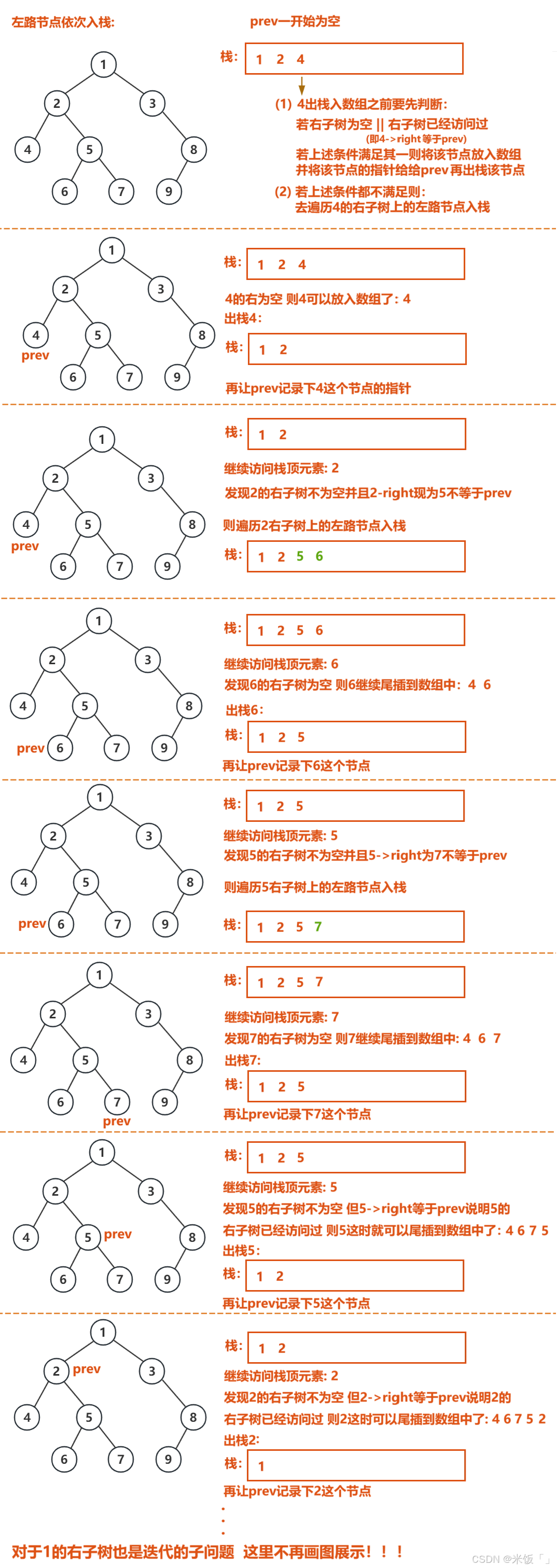
代码实现如下：

class Solution 
{
public:vector<int> postorderTraversal(TreeNode* root) {TreeNode* prev = nullptr;stack<TreeNode*> s;vector<int> v;TreeNode* cur = root;while(cur != nullptr || !s.empty()){//左路节点入栈while(cur){s.push(cur);cur = cur->left;}TreeNode* top = s.top();//top节点的右孩子为空 或者 top的右孩子等于上一个访问的节点//那么说明(空)不用访问 或者 (不为空)右子树已经访问过了if(top->right == nullptr || top->right == prev){v.push_back(top->val);s.pop();prev = top;}else{//右子树不为空 并且 右子树还没有被访问过，则子问题访问右子树cur = top->right;}} return v;  }
};