主题设计师站国内外搜索引擎大全

一、差分

前缀和和差分的核心思想是预处理 ， 可以在暴力枚举的过程中 ， 快速给出查询结果 ， 从而优化时间复杂度 。

最经典的用空间替换时间的做法。

学完差分之后 ， 大家会发现 ， 前缀和与差分是一对互逆的运算

二、一维差分

登录—专业IT笔试面试备考平台_牛客网

解法一：暴力解法 --> 直接模拟

两层 for 循环 -->  O（m*n) = 10^10 (超时了...) 

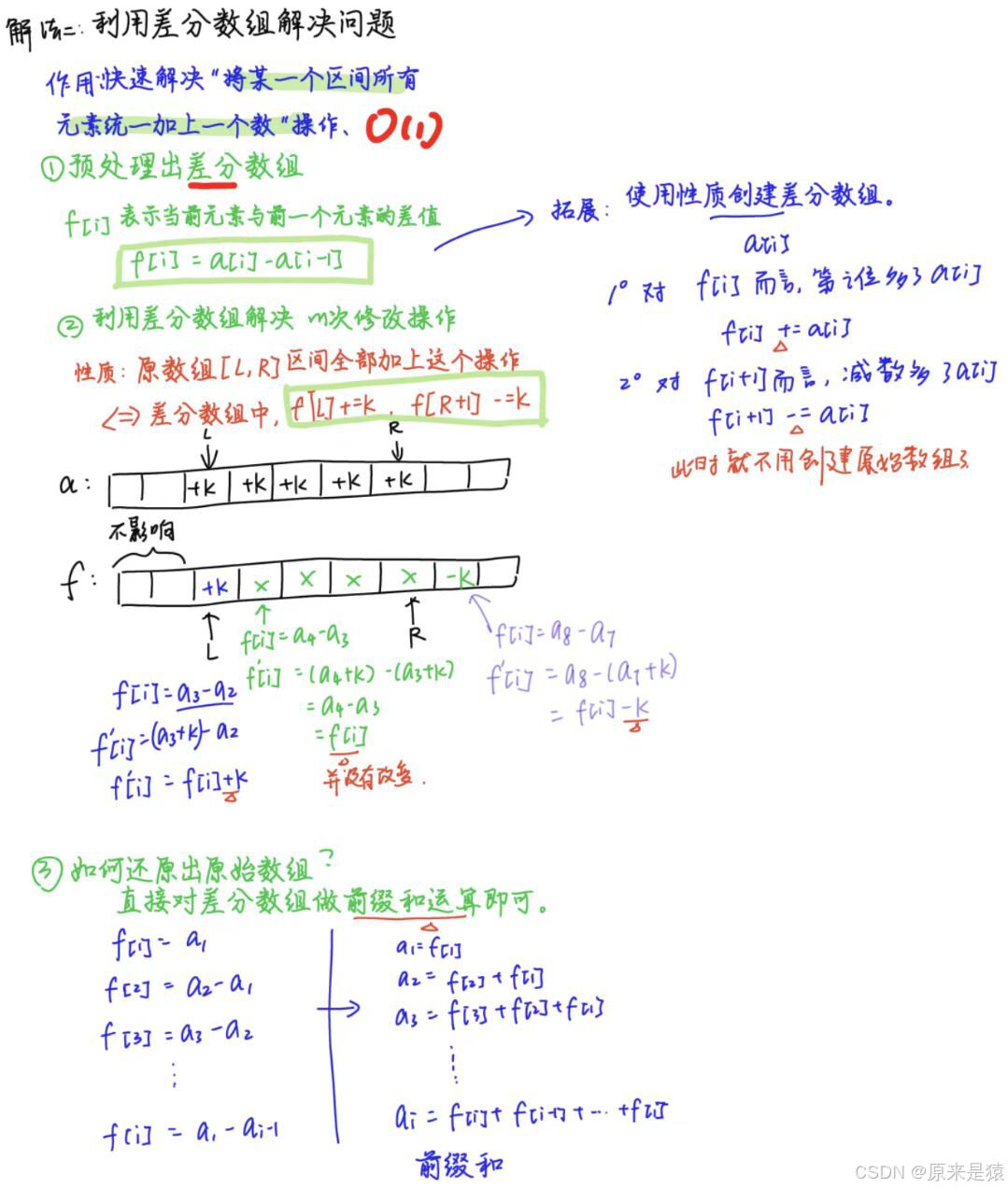
所以我们可以总结出 用差分解决问题的模板：

1） 创建差分数组

 

2）利用差分数组处理 m 次 修改操作

3）还原成原始数组：

#include <iostream>
using namespace std;typedef long long LL;
const int N = 1e5 + 10;
LL n,m;
LL a[N];
LL f[N];//记录差分数组int main()
{cin >> n >> m;//利用差分数组定义创建差分数组for(int i = 1;i<=n;i++){cin >> a[i];f[i] = a[i] - a[i-1];}//处理 m 次修改操作while(m--){LL l,r,k;cin >> l >> r >> k;f[l] += k;f[r+1] -= k;} //还原出原始的数组for(int i = 1;i<=n;i++){a[i] = a[i-1] + f[i];cout << a[i] << " ";}return 0;
}

三、海底高铁

P3406 海底高铁 - 洛谷

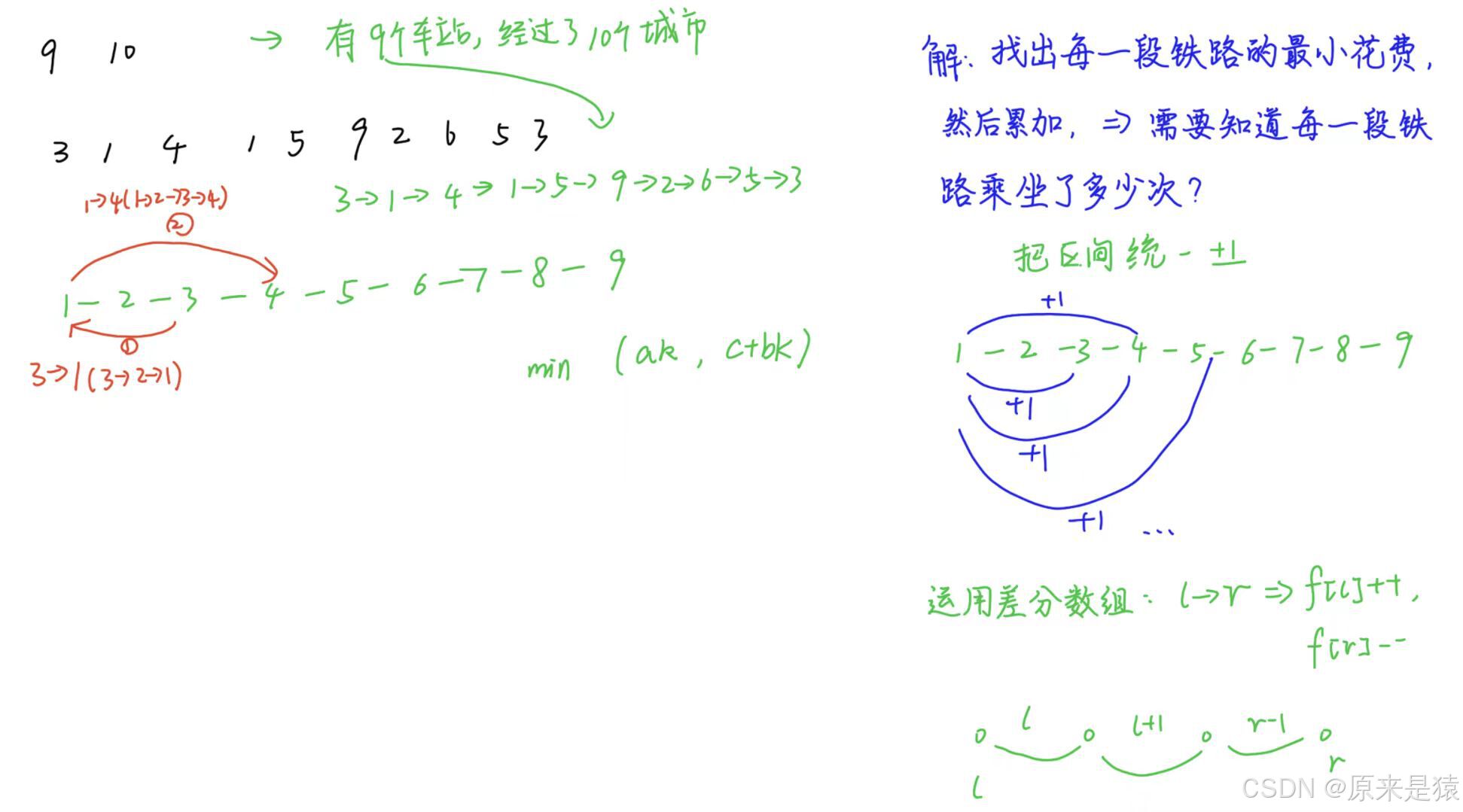
#include <iostream>
using namespace std;typedef long long LL;const int N = 1e5 + 10;int n,m;
LL f[N];//差分数组 int main()
{cin >> n >> m;//x->yint x,y;cin >> x;//处理差分数组 for(int i = 2;i<=m;i++){cin >> y;//x->yif(x > y)f[y]++,f[x]--;else f[x]++,f[y]--;x = y;}//利用差分数组，还原出原数组for(int i = 1;i<=n;i++){f[i] += f[i-1];} //直接求结果LL ret = 0;for(int i = 1;i<=n;i++){LL a,b,c;cin >> a >> b >> c;ret += min(a*f[i],c+b*f[i]);} cout << ret << endl;return 0;} 

四、二维差分

登录—专业IT笔试面试备考平台_牛客网

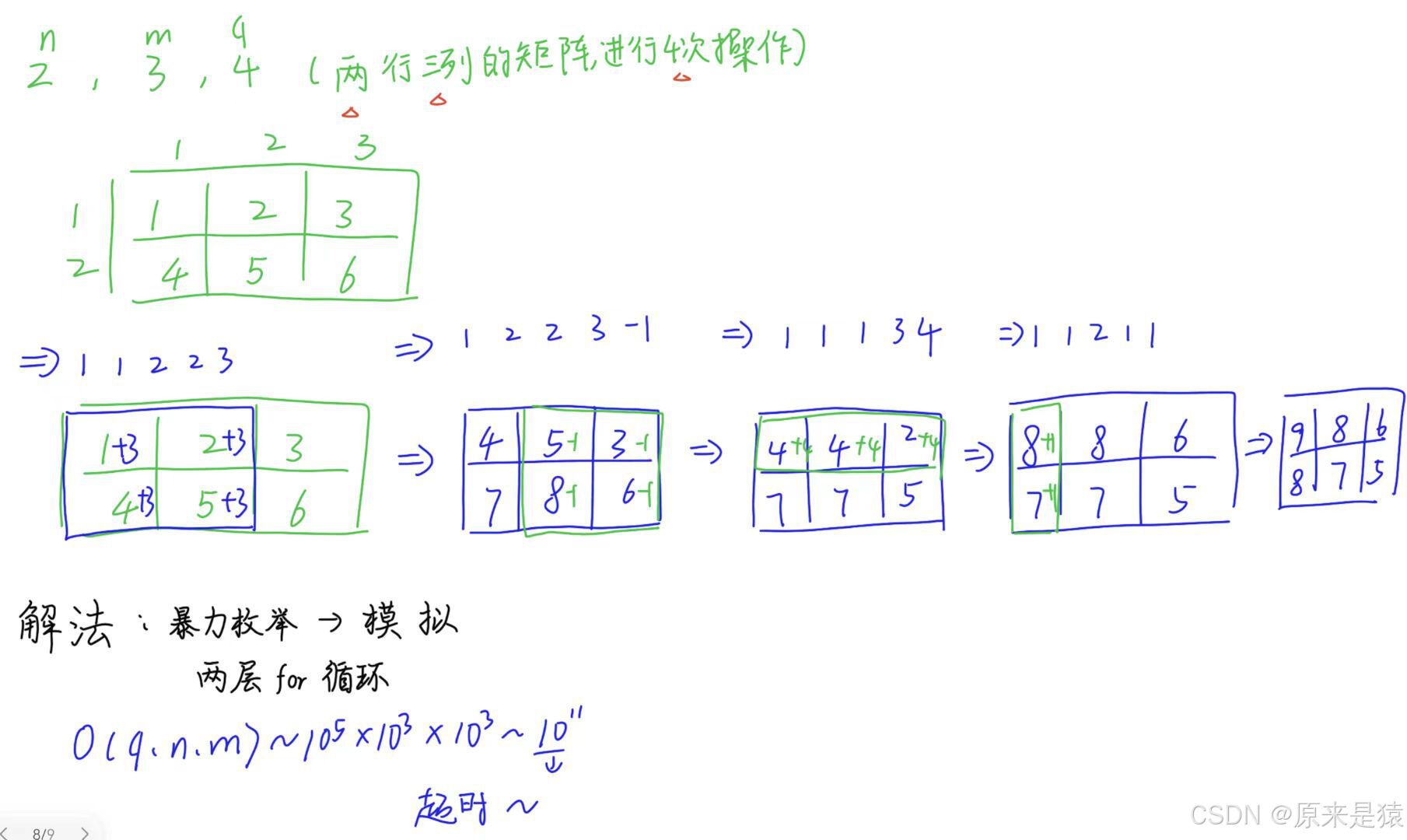
第一个能想到的就是暴力枚举 ， 到了目标区域 ， 直接进行操作，

但是时间复杂度太高了 ， OJ平台是不会给过的~

借助二维差分数组 ：

画图 ！ 了解二维差分数组的性质 ， 等再次使用的时候 ， 上手会很快！！！

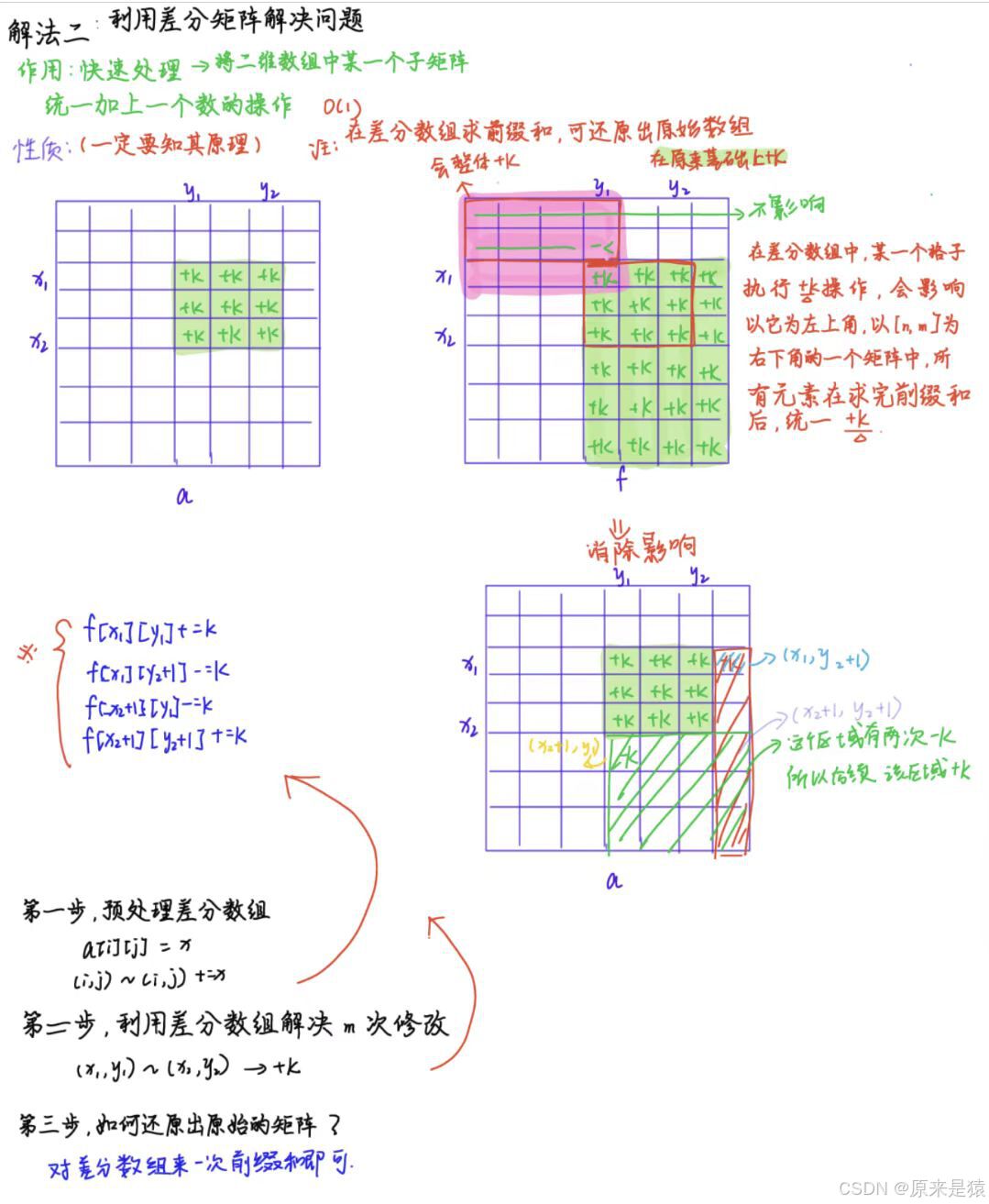
#include <iostream>
using namespace std;typedef long long LL;
const int N = 1001;
LL n,m,q;
LL f[N][N];//差分矩阵 //差分矩阵的性质 
void insert(int x1,int y1,int x2, int y2,int k)
{f[x1][y1] += k;f[x1][y2+1] -= k;f[x2+1][y1] -=k;f[x2+1][y2+1] +=k; 
}int main()
{cin >> n >> m >> q;//预处理--构造差分矩阵 for(int i = 1;i<=n;i++){for(int j = 1;j<=m;j++){LL x;cin >> x;//[i,j] 为左上角，[i,j]为右下角的矩阵，统一加上xinsert(i,j,i,j,x); }}//处理q次修改操作while(q--){int x1,y1,x2,y2,k;cin >> x1 >> y1 >> x2 >> y2 >> k;insert(x1,y1,x2,y2,k);} //利用前缀和还原修改之后的数组for(int i = 1;i<=n;i++){for(int j = 1;j<=m;j++){f[i][j] = f[i-1][j] + f[i][j-1] - f[i-1][j-1] + f[i][j];cout << f[i][j] << " ";}cout << endl;} return 0;
}

五、地毯

P3397 地毯 - 洛谷

差分数组走起来 ， 简简单单~ 

#include <iostream>
using namespace std;const int N = 1010;
int f[N][N];
int n,m; void insert(int x1,int y1,int x2,int y2)
{f[x1][y1]++;f[x2+1][y1]--;f[x1][y2+1]--;f[x2+1][y2+1]++;
}
int main()
{cin >> n >> m;while(m--){int x1,y1,x2,y2;cin >> x1 >> y1 >> x2 >> y2;insert(x1,y1,x2,y2);}//借助前缀和还原成原数组for(int i = 1;i<=n;i++){for(int j = 1;j<=n;j++){	f[i][j] = f[i-1][j] + f[i][j-1] - f[i-1][j-1] + f[i][j];cout << f[i][j] << " ";	}cout << endl;}return 0;
}

 在理解的基础上可以背背 ， 但是尽量不要背 ， 理解为主