徐州鸿美网站建设百度指数热度榜
图
无向图
<V,E>有序二元组,代表一个无向图G
-
V是顶点的集合,元素为顶点;称为顶点集
-
E是边的集合,元素为无向边;称为边集合
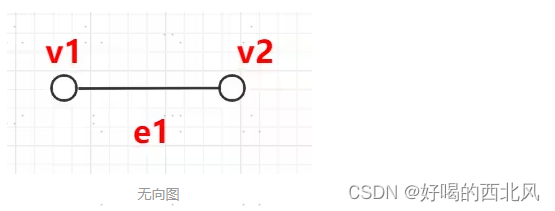
有向图
<V,E>有序二元组,代表一个有向图G
-
V是顶点的集合,元素为顶点;称为顶点集
-
E是边的集合,元素为无向边;称为边集合
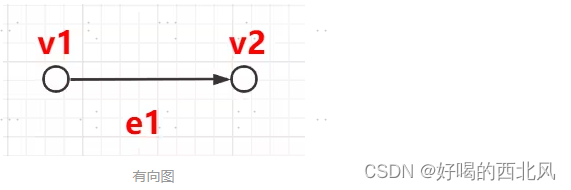
RUN
- 图:有向图+无向图,G代表有向图,D代表无向图
- 阶:定点数,有n个顶点称n阶图
- 零图:只有点没有边,有n个点为n阶零图,记为Nn
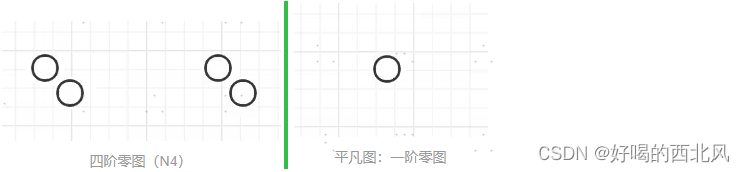
- 空图:顶点集为空(什么也没有),记为 ∅
-
标定图:有符号标识的图
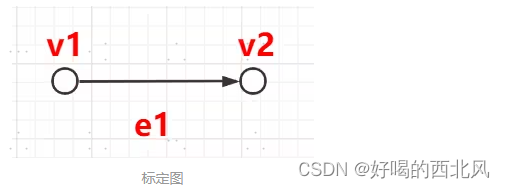
-
非标定图:无符号标识的图
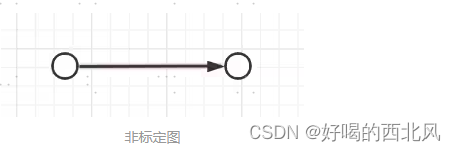
-
基图:有向图原型(无向图)1.1为1.2的基图
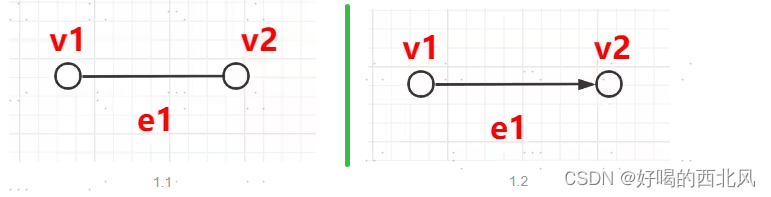
端点
关联
-
无向图:ek = (Vi,Vj)则Vi、Vj为ek的端点(就是一条线两边的点),ek与Vi(Vj)关联
if Vi != Vj ,则ek与Vi(Vj)的关联次数为1(就是一个点只碰了一次这个线)
if vi = vj,则ek与vi(vj)的关联次数为2,并称ek为环(一个点碰了线2次)
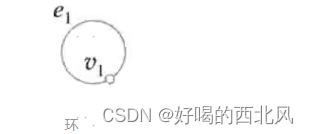
-
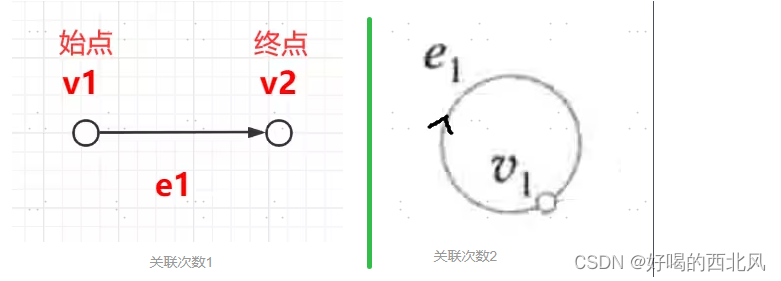
有向图:ek = (vi,vj)则vi,vj为ek的端点,vi为始点,vj为终点,ek 与 vi(vj)关联
if vi ≠ vj,则ek与vi(vj)的关联次数为1(就是一个点只碰了一次这条线)
if vi = vj,则ek与vi(vj)的关联次数为2,并称ek为环(一个点碰了线2次)
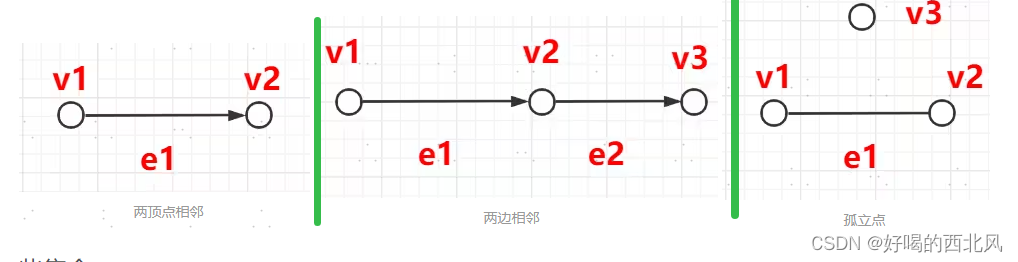
- 相邻:vi 与 vj 有一条边连接,则两顶点相邻,两边至少有一个公共顶点则两边相邻
-
孤立点:V3
一些集合
无向图:G = <V,E>, ∀v∈V
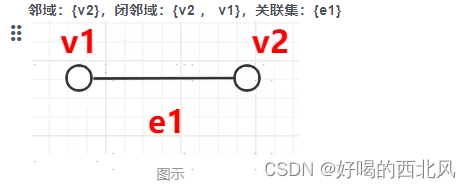
- 邻域:与v1相邻的点的集合(相邻见上)
![]()
-
闭邻域:邻域 + v1(自己)的集合
![]()
-
关联集:与v相关联的边的集合(关联见上)
![]()
有向图:D = <V,E>, ∀v∈V
- 后继元集:从v2出发,到达的点的集合
- 先驱元集:到达v2的出发点的集合
-
邻域:先驱元集+后继元集
-
闭邻域:


-
平行边:一对顶点的无向边多于1条,则为平行边(有向边:方向也需要相同

- 重数:平行边的条数
-
多重图:含平行边的图
-
简单图:不含平行边,不含环的图(在有向图中,相同端点,方向不同的边,不算平行度
-
无向图 G = <V,E>, ∀v∈V
度数:v关联的边的数量(环以v做两次端点),即:dg(v),v点勾搭的边数
G的最大度:G中含有的最大度数
G的最小度:G中含有的最小度数
-
有向图:D = <V,E>, ∀v∈V
出度:v为始点的次数(箭头出去的数量)
入度:v为终点的次数(箭头进来的数量)
度数:出度+入度
-
记牢符号

- 悬挂顶点:度数为1的顶点
-
悬挂边:与悬挂顶点关联的边
-
偶度(奇度)顶点:度为偶数(奇数)的顶点
-
握手定理
无向图:所有顶点的度数之和等于边数的2倍;度数 = 边数*2=2m
有向图:所有顶点的度数之和等于边数的2倍;入度之和 = 出度之和 = 边数

-
度数列:G=<V,E>为一个n阶无向图,V{v1,v2,...,vn},称d(v1),d(v2),...,d(vn)为G的度数列对于顶点标定的无向图,它的度数列是唯一的
-
可图化:度数列的和为偶数,即度数列可图化,反之则不可图化

- 简单可图化,在可图化的基础上,d(vn)max < n,则可实现简单图化

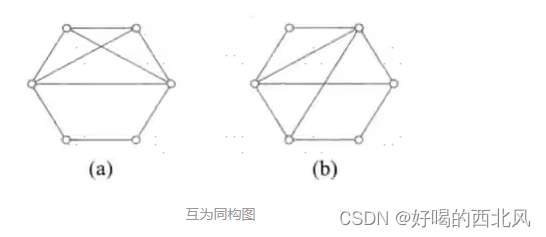
同构
同构图:两个无向图(有向图),具备阶数相同,边数相同,度数列相同等条件。
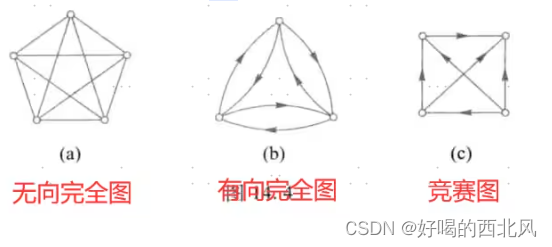
完全图&竞赛图
-
完全图:G为n阶简单图,图内每个顶点与其余顶点都相邻(每个点都有线相连)
则G为n阶无向(有向)完全图
-
竞赛图:D为n阶有向简单图,若基图是无向完全图,则其为竞赛图
母图&导出子图
- 类似于父集与子集的关系
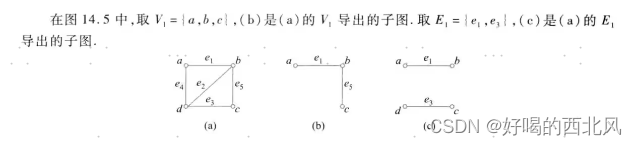
- 以产生原因分辨图为V1/E1的导出子图
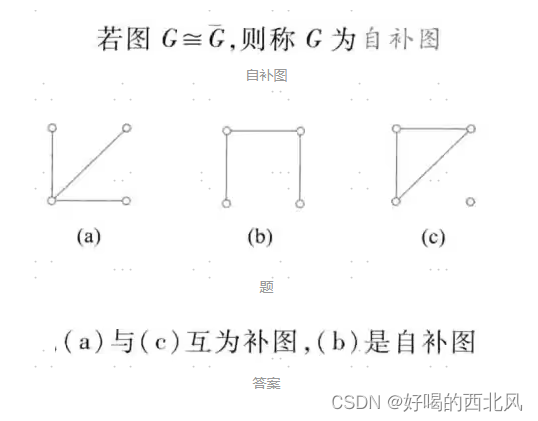
补图

人话:
与G含有相同顶点,能够使G补成完全图的图,为G的补图
通路与回路
- 通路:即一个点到另一个点,所走的路径
-
vi0与vil即为通路的始点与终点
-
其中边的条数为通路的长度
-
若vi0 = vil,则为回路
-
若经过的边没有重复,则为简单通路(回路),反之则为复杂回路(通路)
-
若经过的顶点没有重复,则为初级通路/路径(初级回路/圈)
-
长度为奇数,称奇圈,为偶数,称偶圈
图的连通性
-
连通:无向图G = <V,E>,若两顶点之前存在通路,则称两点连通,即u~v, d(vi , vi)
-
连通图:即无向图G = <V,E>任何两个顶点都是连通的
注意!!!
与完全图存在区别,连通指的是能从这个点走到那个点就好,完全图则需要任意两个顶点都要有边
完全图(n >= 1)都是连通图
零图(n >= 2)都是非连通图
-
短程线(距离):即两点间的最短通路
-
割集:在连通图中删去某些边,某些点,使连通图变得不连通
-
点割集:在原图中删去顶点的集合,使连通图变得不连通
-
割点:点割集中只有一个顶点v
-
边割集:在原图中删去边的集合,使连通图变得不连通
-
割边/桥::点割集中只有一条边e
-
点连通度:最小删掉的顶点数
无向完全图的点连通度为:n-1
非连通图:0
k-连通图:点连通度为k
-
边连通度:最小删掉的边数
-
无向完全图的边连通度为:n-1
-
非连通图:0
-
r-边连通图:边连通度为r
-
点连通度 <= 边连通度 <= 最小度
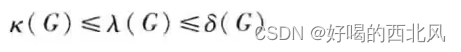
- 有向图的连通性:∀vi , vi∈V,表示方法有所不同 d<vi , vi>
