网站中数据查询如何做网络营销的培训课程

1. 题目链接

1039. 多边形三角剖分的最低得分 - 力扣（LeetCode）

2. 题目描述

你有一个凸的 n 边形，其每个顶点都有一个整数值。给定一个整数数组 values ，其中 values[i] 是第 i 个顶点的值（即 顺时针顺序 ）。

假设将多边形 剖分 为 n - 2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。

返回 多边形进行三角剖分后可以得到的最低分 。

3. 题目示例

示例 1 :

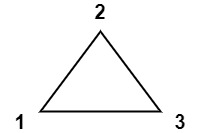
输入：values = [1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6

示例 2 :

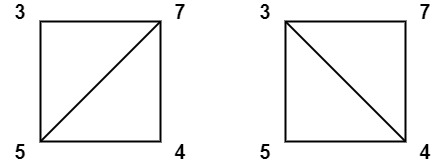
输入：values = [3,7,4,5]
输出：144
解释：有两种三角剖分，可能得分分别为：3*7*5 + 4*5*7 = 245，或 3*4*5 + 3*4*7 = 144。最低分数为 144。

示例 3 :

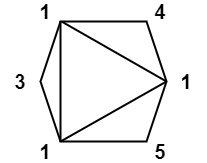
输入：values = [1,3,1,4,1,5]
输出：13
解释：最低分数三角剖分的得分情况为 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13。

4. 解题思路

1. 问题理解：
   • 给定一个凸多边形的顶点值数组，需要将其三角剖分成若干个三角形
   • 每个三角形的得分为三个顶点值的乘积
   • 目标是找到使所有三角形得分之和最小的三角剖分方式
2. 动态规划思路：
   • 定义memo[i][j]表示从顶点i到j的最小三角剖分分数
   • 基本情况：当i和j相邻时（只有两个顶点），无法形成三角形，得分为0
   • 状态转移：枚举所有可能的中间顶点k（i < k < j），将多边形分成左右两部分
     • 总得分 = 左部分得分 + 右部分得分 + 当前三角形得分（v[i]*v[j]*v[k]）
     • 取所有可能k中的最小值
3. 记忆化搜索：
   • 使用记忆数组存储已计算结果，避免重复计算
   • 自顶向下的递归方式，结合记忆化实现动态规划
4. 关键点：
   • 如何选择中间顶点k将多边形分成最优的两部分
   • 通过递归分解问题，最终合并子问题的解

5. 题解代码

class Solution {public int minScoreTriangulation(int[] values) {int n = values.length;// 记忆化数组，memo[i][j]表示从顶点i到j的最小三角剖分分数int[][] memo = new int[n][n];// 初始化记忆数组为-1，表示未计算for (int[] row : memo) {Arrays.fill(row, -1);}// 从第一个顶点到最后一个顶点开始计算return dfs(0, n - 1, values, memo);}private int dfs(int i, int j, int[] v, int[][] memo) {// 基本情况：如果只有两个顶点，无法形成三角形，得分为0if (i + 1 == j) {return 0;}// 如果已经计算过，直接返回结果if (memo[i][j] != -1) {return memo[i][j];}// 初始化结果为最大值int res = Integer.MAX_VALUE;// 遍历所有可能的中间顶点k（i < k < j）for (int k = i + 1; k < j; k++) {// 递归计算左右两部分的最小分数，加上当前三角形的分数res = Math.min(res, dfs(i, k, v, memo) +    // 左边部分dfs(k, j, v, memo) +    // 右边部分v[i] * v[j] * v[k]);    // 当前三角形}// 存储计算结果到记忆数组return memo[i][j] = res;}
}

6. 复杂度分析

时间复杂度：O(n³)

• 共有O(n²)个子问题（i,j组合）
• 每个子问题需要O(n)时间枚举k
• 总时间复杂度为O(n³)

空间复杂度：O(n²)

• 用于存储记忆数组memo[n][n]