排序--快排--挖坑法
一,引言
快排的挖坑法是对hoare的一种改进,有想法的同学可以了解一下,下面进行挖坑法的逻辑讲解和函数实现。
二,逻辑讲解
首先看一组动图:
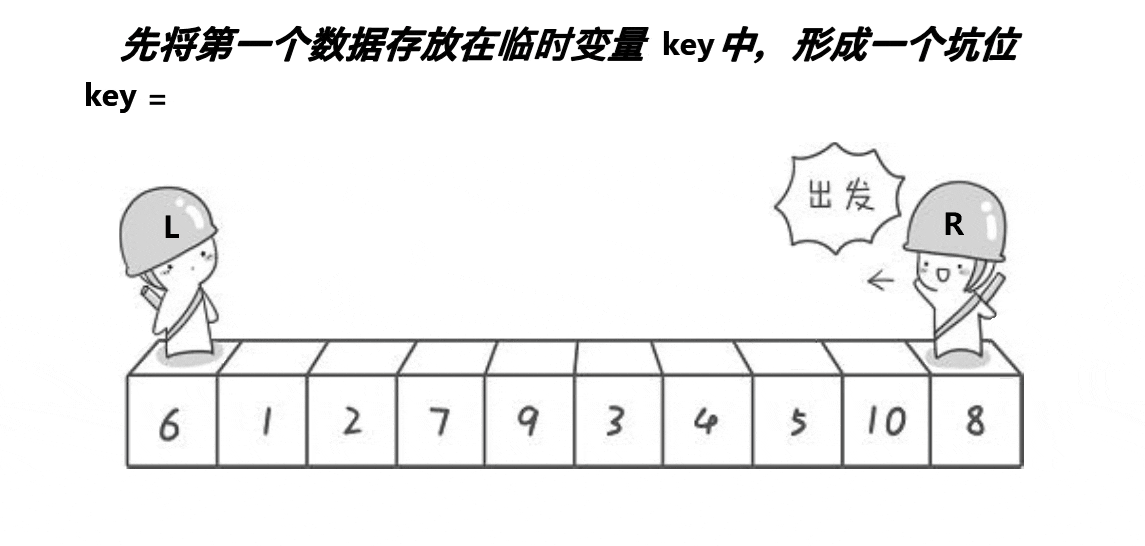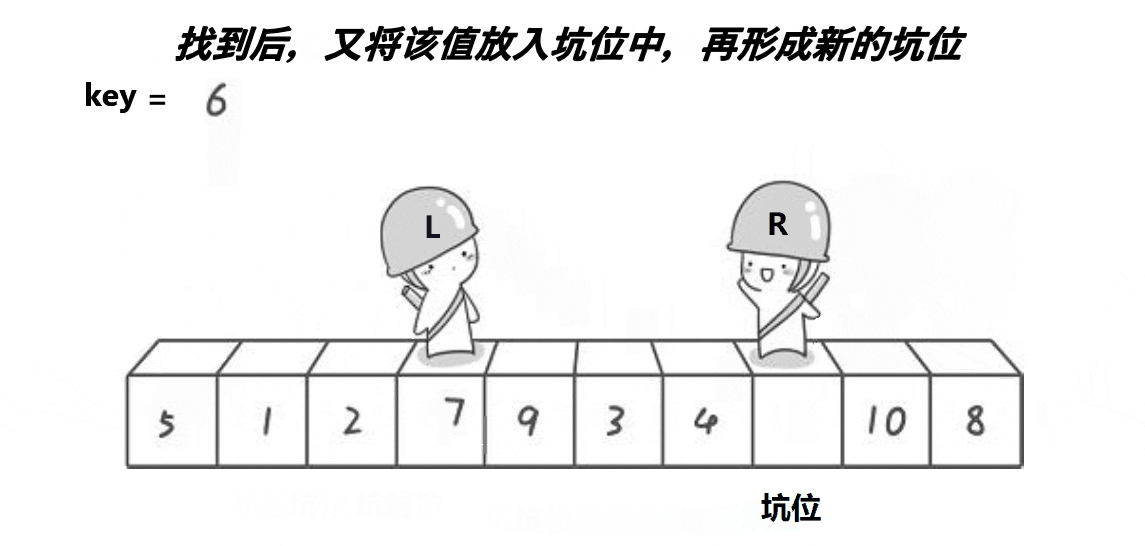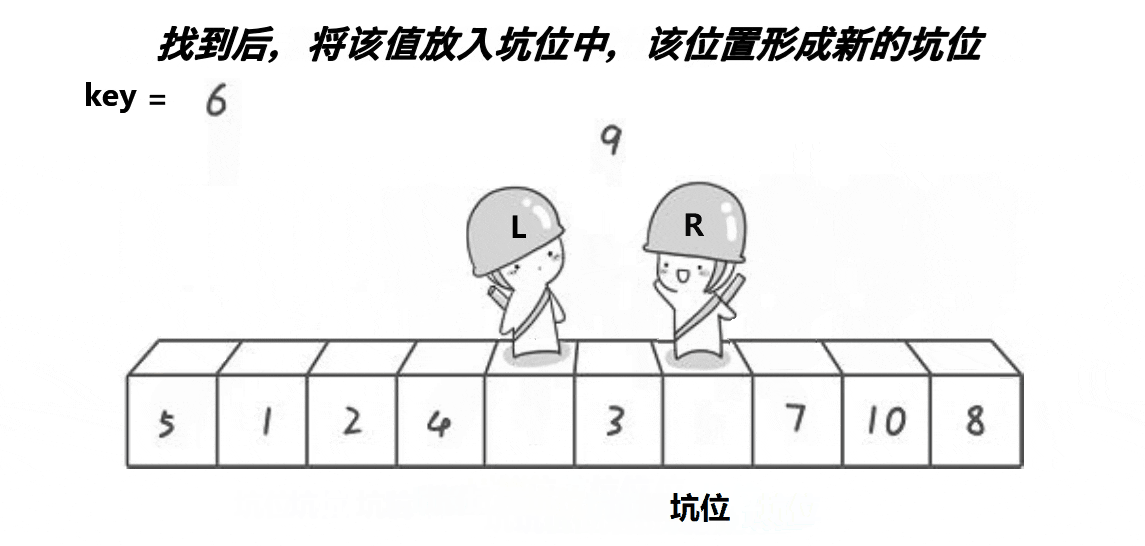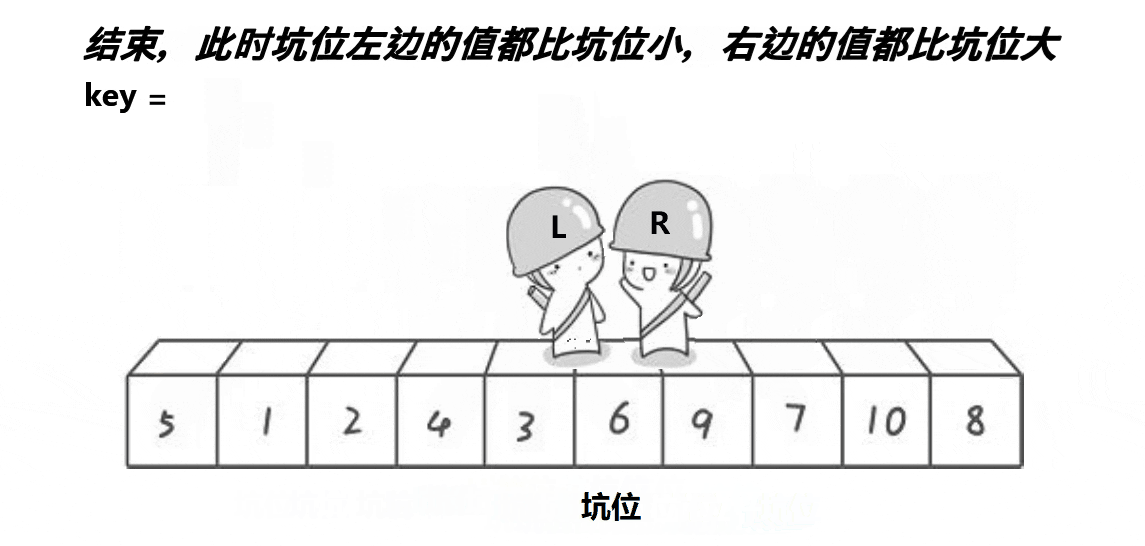
总括:首先讲key位置的值进行标记保存,此时key位置为坑,用一个标量来标记坑的位置。之后,从右开始比key小的值,找到之后,于坑的位置进行交换,交换之后,这个位置成为新的坑,之后从左开始找比key标记的值大的值,找到之后于坑的位置进行交换,该位置成为新的坑位。依次往复。整个过程于hoare的比较过程相似,判断条件也是相遇时停下。
第一步:

标记key的值和坑位,R从右开始找比key的值小的数,找到之后该值和坑位进行交换,该位置成为新的坑位。
第二步:

L开始向前走找比key大的数,找到之后于坑位进行交换,该位置成为新的坑位。
第三步:
 上述过程交替执行直到LR相遇,将该位置进行赋值,为key的值,以达到key左边都比key的值小右边都比key的值大。
上述过程交替执行直到LR相遇,将该位置进行赋值,为key的值,以达到key左边都比key的值小右边都比key的值大。
之后以key为界限分成两组分别进行递归运行,代码和hoare法完全一致,这里不进行详细讲解,有需要的可以看往期文章有详细讲解。
四,代码实现:
void QuickSort3(int* p, int left, int right)
{
if (left >= right)
{
return;
}
int begin = left;
int end = right;
int keys = p[begin];
int hole = begin;
while (begin != end)
{
while ((keys <= p[end]) && begin != end)
{
end--;
}
swap(&p[hole], &p[end]);
hole = end;
while ((keys >= p[begin]) && begin != end)
{
begin++;
}
swap(&p[hole], &p[begin]);
hole = begin;
}
keys = begin;
QuickSort3(p, left, keys - 1);
QuickSort3(p, keys + 1, right);
}五,总结
挖坑法和hoare法和双指针法的代码优化和递归逻辑,时间复杂度,空间复杂度,稳定性等都完全一致,这里不进行详细讲解,具体可以去参考hoare法和双指针法。三者仅仅是单趟排序略有不同,大思路都是一致的。
