蓝桥备赛(27)算法篇【二分算法】
一 、 二分算法
二分算法的难点在于对各种各样的细节问题 。所以 , 就算你把二分算法的模板背熟了,但是忽略了各种乱七八糟的边界问题 , 也很难全都AC
那么,我借助下面的OJ题 , 说明一下 需要处理的一些小细节:
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)


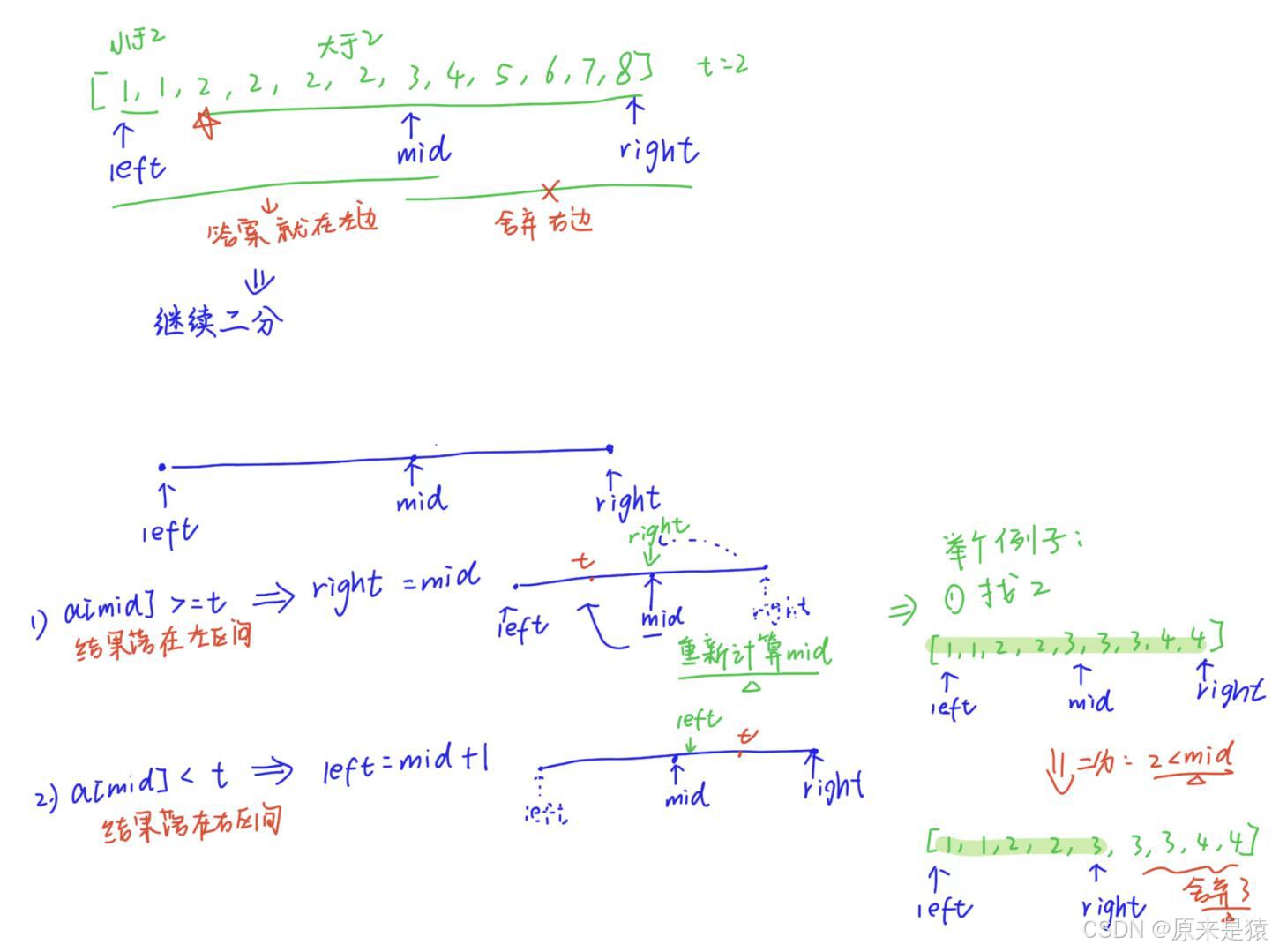

在查找起始位置的时候 , 需要处理一些细节问题:
- while 循环里面的判断如何写?
- 求中点的方式?
- 二分结束后 , 相遇点的情况是什么?
需要考虑清楚 , 分析明白 , 不要带有未经过 证实的惯性思维!!!!

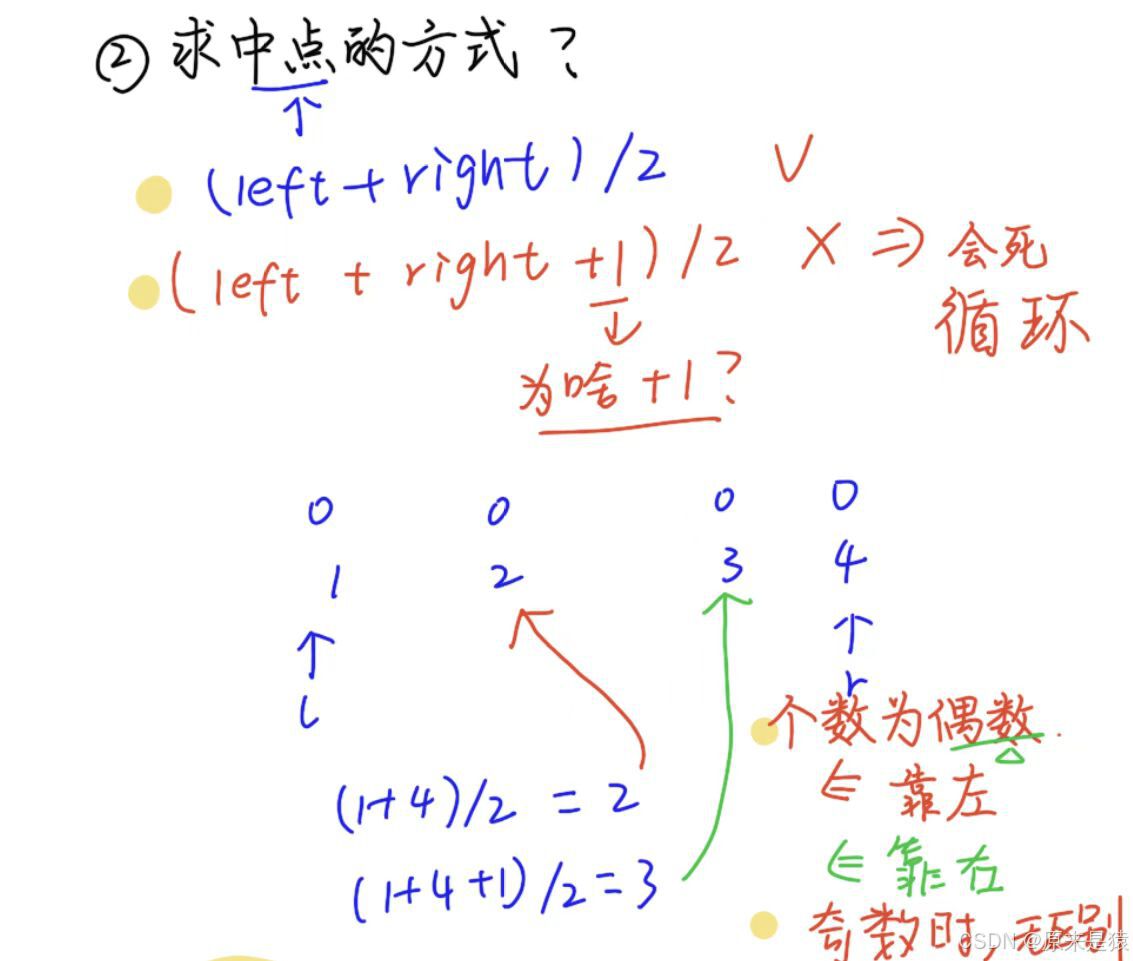


在查找 终止位置的时候 , 需要处理一些细节问题:
- while 循环里面的判断如何写?
- 求中点的方式?
需要考虑清楚 , 分析明白 , 不要带有未经过 证实的惯性思维!!!!


class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int n = nums.size();
//处理一下边界情况
if(n == 0)return{-1,-1};
//1.求起始的位置
int left = 0,right = n-1;
while(left < right)
{
int mid = (left + right) / 2;
if(nums[mid] >= target)right = mid;
else left = mid+1;
}
//left 或者 right 所指的位置就有可能是最终结果
if(nums[left]!=target)return{-1,-1};
int retleft = left;//记录起始位置
//2.求终止位置
left = 0,right = n-1;
while(left<right)
{
int mid = (left + right+1)/2;
if(nums[mid]<=target)left = mid;
else right = mid-1;
}
int retright = right;//记录最终位置
return {retleft,retright};
}
};借助上面的题目 , 我们了解了二分算法,这里总结一下:
当我们的解具有二段性的时候 , 就可以使用二分算法找出答案:
1)根据待查找区间的中间位置 , 分析答案会出现在那一侧;
2)接下来舍弃一半的待查找区间 ,转而在有答案的区间内继续使用二分查找结果!
二分的模板在网上至少能搜出来三个以上。但是,我们仅需要掌握一个,并且一直使用下去即可。
下面介绍一种,其他的可以去搜搜看~


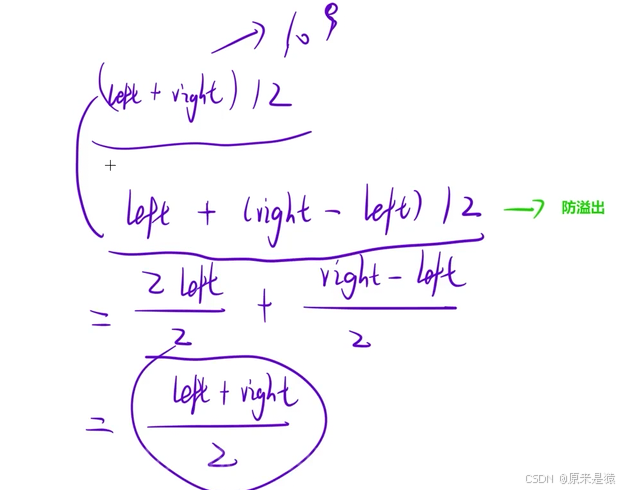
1 . 为了防止溢出,求中点时 可以使用下面的方式:
mid = l + ( r - l ) / 2 ;
2. 时间复杂度 : 每次二分都会去掉一般的查找区域(就是 嘎掉一般的数据了...) , 因此时间复杂度 为 log N
3. 【怎么记忆模板?】
不用死记硬背 , 算法原理搞清楚之后 , 在分析题目的时候 , 自然而然就知道怎么写二分的代码了 , 而且 , 在不同的题目 , 边界情况也是不同的 , 需要具体情况具体分析。e
4. 【二分问题解决流程】
1)先画图分析,确定使用左端点模板 还是 右端点模板 , 还是两者配合一起使用
2)二分出结果之后 , 不要忘记判断结果是否存在 , 二分问题细节很多 , 一定一定一定要分析全面!!!
5. 【STL中二分查找】
<algorithm>
1) lower_bound : 大于等于 x 的最小元素 , 返回的是迭代器 , 时间复杂度:O(log N)
2) upper_bound : 大于 x 的最小元素 , 返回的是迭代器 , 时间复杂度:O(log N)
二者均采用二分实现。但是STL中的二分查找 , 只能适用于 “ 在有序的数组中查找 ” ,如果是二分答案就不能使用 。
二、二分查找
2.1 牛可乐与魔法封印
登录—专业IT笔试面试备考平台_牛客网


#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int n,q;
int binary_search(int x,int y)
{
//1.找大于等于x 的起始位置
int left = 1,right = n;
while(left < right)
{
int mid = (right + left)/2;
if(a[mid] >= x) right = mid;
else left = mid + 1;
}
//处理数组中不存在大于等于 x 的情况
if(a[left] < x) return 0;
int tmp = left;
//2. 找小于等于y 的终止位置
left = 1,right = n;
while(left < right)
{
int mid = (left + right + 1 )/2;
if(a[mid] <= y) left = mid;
else right = mid - 1;
}
//处理数组中不存在小于等于 y 的情况
if(a[left] > y) return 0;
return left-tmp+1;
}
int main()
{
cin >> n;
//输入
for(int i = 1 ;i<=n;i++)cin >> a[i];
//q次询问
cin >> q;
while(q--)
{
int x,y;
cin >> x >> y;
cout << binary_search(x,y) << endl;
}
return 0;
}2.2 A-B数对
P1102 A-B 数对 - 洛谷


这里我们用一下STL :
1) lower_bound: 传入要查询区间的左右迭代器 (注意是左闭右开的区间 , 如果是数组就是左右指针 ) 以及要查询的值 k , 然后返回该数组中 >= k 的第一个位置;
2)upper_bound: 传入要查询区间的左右迭代器 (注意是左闭右开的区间 , 如果是数组就是左右指针 ) 以及要查询的值 k , 然后返回该数组中 > k 的第一个位置;


#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 2E5 + 10;
LL a[N];
LL n,c;
int main()
{
cin >> n >> c;
for(int i = 1;i<=n;i++)cin >> a[i];
//1.排序
sort(a+1,a+1+n);
//2.b = a - c
LL ret = 0;
for(int i = 2 ; i<= n ;i++)
{
LL b = a[i] - c;
ret += upper_bound(a+1,a+i,b) - lower_bound(a+1,a+i,b);
}
cout << ret << endl;
return 0;
}2.3 烦恼的高考志愿
P1678 烦恼的高考志愿 - 洛谷


#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL a[N];;
int n,m;
int find(LL x)
{
int left = 1,right = m;
while(left < right)
{
int mid = (left + right)/2;
if(a[mid] >= x)right = mid;
else left = mid + 1;
}
return left;
}
int main()
{
cin >> m >> n;
for(int i = 1;i<=m;i++)cin >> a[i];
//1.排序
sort(a+1,a+m+1);
//2.二分
//加上左右护法
a[0] = -1e7 + 10;
LL ret = 0;
while(n--)
{
LL x;
cin >> x;
int pos = find(x);
ret += min(abs(a[pos] - x),abs(a[pos-1] - x));
}
cout << ret << endl;
return 0;
}三、二分答案
准确来说,应该叫做【二分答案 + 判断】
3.1 木材加工
P2440 木材加工 - 洛谷



#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
LL n,k;
const int N = 1e5 + 10;
LL a[N];
//当切割长度为 x 的时候,最多能切除多少段
LL calc(LL x)
{
LL ret = 0;
for(int i = 1;i<=n;i++)
{
ret += a[i]/x;
}
return ret;
}
int main()
{
cin >> n >> k;
//1.输入
for(int i = 1;i<=n;i++)cin>>a[i];
//2.排序
sort(a+1,a+1+n);
//3.二分
LL left = 0,right = 1e8;
while(left < right)
{
LL mid = (left + right + 1 )/2;
LL c = calc(mid);
if(c >= k) left = mid;
else right = mid-1;
}
cout << left << endl;
return 0;
}3.2 砍树
P1873 [COCI 2011/2012 #5] EKO / 砍树 - 洛谷

#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
LL n,m;
LL a[N];
LL calc(LL x)
{
LL cnt = 0;
for(int i = 1;i<=n;i++)
{
if(a[i] > x)cnt += a[i] - x;
}
return cnt;
}
int main()
{
cin >> n >> m;
//1.输入
for(int i = 1;i<=n;i++)cin >> a[i];
//2.排序
sort(a+1,a+1+n);
//3.二分
LL left = 1,right = 2e9;
while(left < right)
{
LL mid = (left + right + 1) / 2;
LL c = calc(mid);
if(c >= m)left = mid;
else right = mid - 1;
}
cout << left << endl;
return 0;
}3.3 跳石头
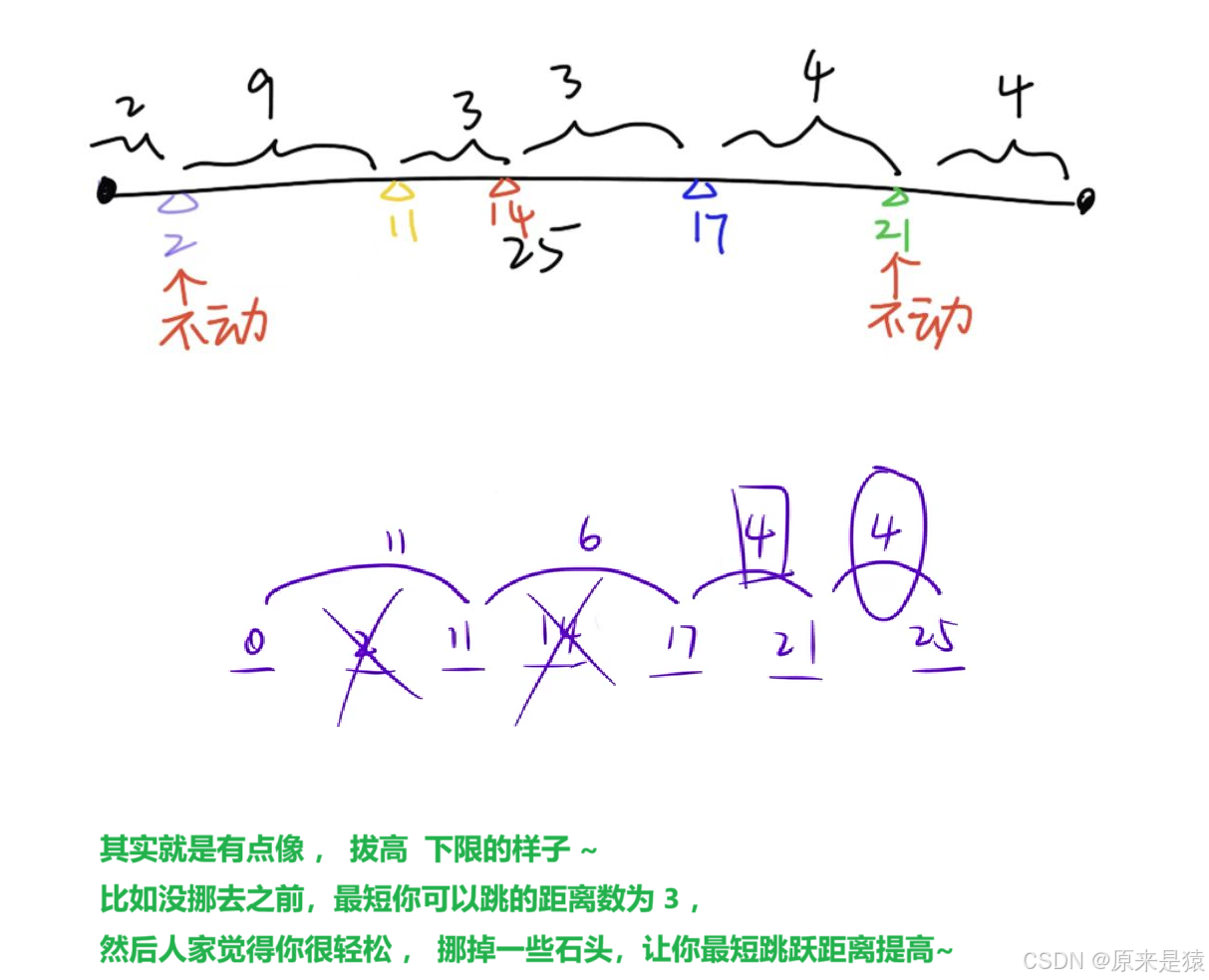
P2678 [NOIP 2015 提高组] 跳石头 - 洛谷


#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 5e4 + 10;
LL l,n,m;
LL a[N];
//当最短跳跃距离为x , 所能移走的岩石数
LL calc(LL x)
{
LL ret = 0;
for(int i = 0;i<=n;i++)
{
int j = i+1;
while(j <= n && a[j] - a[i] < x)j++;
ret += j-i-1;
i = j-1;
}
return ret;
}
int main()
{
cin >> l >> n >> m;
//1.输入
for(int i =1 ;i<=n;i++)cin >> a[i];
a[n + 1] = l;
n++;
//2.二分
LL left = 1,right = l;
while(left < right)
{
LL mid = (left + right + 1) /2;
if(calc(mid) <= m)left = mid;
else right = mid - 1;
}
cout << left << endl;
return 0;
}