自然数k次方的前n项和通项公式

前言

西江月 证明
即得易见平凡，仿照上例显然。留作习题答案略，读者自证不难。
反之亦然同理，推论自然成立，略去过程QED，由上可知证毕。

笔者在日常学习中饱受“显然”、“易证”困扰，遂开此专栏整理了一些命题的详尽证明思路，不定期更新，毕竟公式打起来真是要人老命~

本文主要推导以下表达式的通项公式

k=1

此时

调换顺序

于是

化得

k=2

此时

进行如下变换

即

进一步展开

解得

以上推导涉及到了乘方运算、乘法运算的本质，是一种较为巧妙的数学组合方法。对于更高次幂的计算，此方法需要有较好的几何思维（维度更高，更加复杂），此时不妨将视线转向以上推导的关键式：

此式本质在于将难以计算的自然数高次幂之和用自然数较低次幂之和表示：通过已知（易知）推导未知是一种通用的思维方式（例如递推公式）。我们似乎触碰到了解决该问题的核心思路：是否可以构造这样一个方程，同时包含已知的、结构相近的与未知的的方程？

k=2? k=3!

我们可以轻易的想到平方公式：

在本例中可表示为时有

更一般的，我们将平方公式推广

其中

在本例中可表示为时有

 其中

整理代回

展开

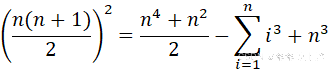
 进一步化简

于是我们便推导……等会，我们原本的目标是什么来着？阴差阳错的，我们先一步推导出了，且发现其是的平方。

既然以上的方法“失效”了，那么通过立方是否可以达成“凑方程”的目标呢？为了保证推导的独立性，我们不能使用已经推导出的。对于立方展开，可通过以下表达式消除掉立方项：

则

实际上经过裂项相消后只剩下

代回原方程经过化简后可得

至此，我们成功推导出时的，且找到了一种通用的推导方法，接下来按部就班推导至一般即可。以下将给出任意的通项公式

k=k

设

对式子两边同时求和得

根据二次项展开定理：

我们需要关注（用于消除）与（用于做方程未知数）的系数，于是进一步展开得

原式变换为

整理得

综上，自然数k次方的前n项和通项公式为

后语

附上笔者推导过程丑照（笔误与推导冗余之处在上文中已经修改）

特别感谢【数玩の日常003】自然数 k 次方前n项和通项公式③ - 知乎提供的一种解决思路。