微积分小白入门:第二章 数列与极限——从困惑到顿悟的奇妙之旅
微积分小白入门:第一章 数列与极限——从困惑到顿悟的奇妙之旅
一、为什么从数列开始?
高中数学中,我们学过数列的基本概念,比如等差数列、等比数列。大学微积分的起点,正是从这些熟悉的数列出发,但视角却发生了质的变化。想象你站在海边,数列像不断涌来的浪花,而极限则是浪花最终触及的岸边线。高中阶段我们只关心浪花的规律(如每一波的高度),但大学要研究的是浪花如何无限接近岸边——这正是微积分的核心思想。
二、数列:从具体到抽象的跨越
高中视角

大学视角

对比示例

三、极限:从“差不多”到“严格证明”
高中理解

大学定义(ε-N语言)

通俗翻译

四、收敛与发散:数列的两种命运

极限唯一性(反证法得出)、单调有界必收敛、
典型案例

五、极限的三大武器
1. 夹逼定理(三明治定理)
- 高中应用:通过观察数列的上下界估计极限。
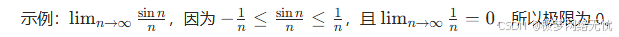
2. 单调有界定理
- 大学定理:单调递增且有上界的数列必收敛。

3. 极限的四则运算

六、高中生的常见误区
-
“极限必须属于数列本身”

-
“无限接近就是相等”

-
“发散数列一定趋向无穷大”

七、学习建议:从具体到抽象

八、总结与预告
数列与极限是微积分的“语言入门课”。高中阶段我们学会了数列的计算,大学则要用严格的数学语言(如ε-N定义)描述“无限接近”。下一章,我们将走进函数的极限,探索连续与间断的奥秘,并解锁微积分的核心工具——导数!
练习挑战
- 证明
lim_{n→∞} (n² + 3n)/(2n² - 5) = 1/2。 - 研究数列
a_n = √(n+1) - √n的极限(提示:分子有理化)。
记住:数学的海洋看似深不可测,但每一滴水的轨迹,都遵循着极限的法则。🚀
